Symetria punktowa istnieje wtedy, gdy figura jest narysowana wokół jednego punktu.

Ten punkt nazywamy środkiem figury lub środkiem symetrii. Na sąsiednim rysunku widzimy, że odpowiadającemu punktowi X na figurze, istnieje punkt X’ po drugiej stronie środka, który jest wprost przeciwny do punktu X i leży na figurze. Mówimy, że figura jest symetryczna względem środka.
Uwaga:
Gdy obrócimy figurę o 180° i odzyska ona swój pierwotny kształt, to mówimy, że istnieje w niej symetria punktowa.
Przykłady figur wykazujących symetrię punktową:
● Wszystkie litery alfabetu angielskiego.
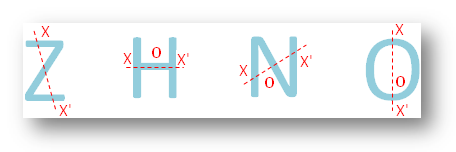
● Różne figury geometryczne.
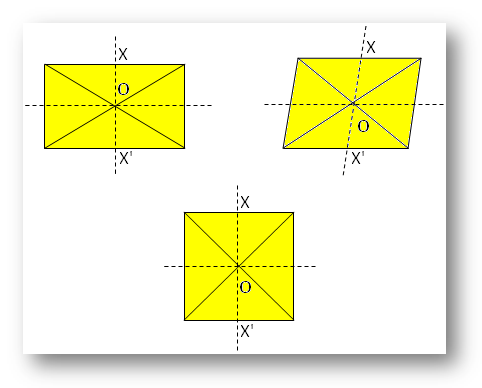
Uwaga:
Tutaj, O jest środkiem symetrii.
W odniesieniu do X istnieje X’, taki, że X’ jest bezpośrednio naprzeciwko X po drugiej stronie O.
Jakie warunki spełnia kształt lub figura dla symetrii punktowej?
Warunki, które spełnia kształt lub figura dla symetrii punktowej, tzn. każda część powinna mieć odpowiadającą jej część
– odległość powinna być jednakowa od punktu środkowego
– ale powinna być w przeciwnym kierunku.
● Pojęcia pokrewne
● Symetria liniowa
● Linie symetrii
● Symetria obrotowa
● Kolejność symetrii obrotowej
● Rodzaje symetrii
● Odbicie
● Odbicie punktu w osi x-.oś
● Odbicie punktu w osi y
● Odbicie punktu w początku
● Obrót
● Obrót o 90 stopni w prawo
● Obrót o 90 stopni w lewo
● Obrót o 180 stopni
.
Problemy matematyczne dla siódmej klasy
Ćwiczenia matematyczne dla ósmej klasy
Od symetrii punktów do STRONY GŁÓWNEJ
.