Zanim zaczniemy, musimy przyjąć pewne założenia.
Po pierwsze, pracujemy z płynami newtonowskimi. Jest to najprostszy matematyczny sposób na uwzględnienie lepkości w płynie. Nie ma rzeczywistych płynów, które idealnie mieszczą się w tej kategorii, ale w większości przypadków powietrze i woda mogą być traktowane jako płyny newtonowskie. Inną bardzo ważną hipotezą, którą stawiamy, jest to, że płyn jest nieściśliwy. Oznacza to, że jego gęstość, rho, jest stałą.
Zachowanie masy

Pierwsze równanie mówi nam, że masa płynu, nad którym pracujemy, jest zachowana. Płyn może zmienić swój kształt, ale to równanie mówi nam, że jego masa jest taka sama od początku do końca.
Teraz porozmawiajmy o matematyce. Litera u reprezentuje prędkość płynu i jest wektorem. Ma trzy składowe, możemy je nazwać u, v, w i reprezentują one prędkość płynu w kierunkach x, y i z. Grecka litera nabla ∇ po której następuje kropka jest operatorem dywergencji. Oznacza to, że musimy różniczkować jego składowe w każdym kierunku (w tym przypadku x, y, z).

Pierwsza pochodna mówi nam, jak zmienia się składowa x prędkości, gdy poruszamy się w kierunku x. Podobnie jest z pozostałymi dwiema pochodnymi. To samo dotyczy dwóch pozostałych pochodnych. Ponieważ równanie to jest równe zeru, pokazuje nam, że masa jest zachowana.
Zachowanie pędu

Drugie równanie jest tak naprawdę zbiorem trzech równań różniczkowych. To właśnie ono może być opisane jako drugie prawo Newtona dla płynów. Jeśli rozszerzymy wyrażenie, otrzymamy układ złożony.
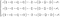
Ponieważ jest ono dużo prostsze do zrozumienia, skupimy się na zachowaniu pędu nie rozszerzonym.
Gdy pracujemy z płynami możemy powiedzieć, że masa i gęstość to te same rzeczy (tak długo jak ich objętość jest taka sama). Jeśli rozważamy dwa płyny, możemy powiedzieć, że gęstszy z nich jest „cięższy” (np. rtęć i woda). W tym przypadku grecka litera ρ (rho) oznacza gęstość płynu.
Mamy masę, teraz aby wrócić do drugiego prawa Newtona potrzebujemy przyspieszenia. To jest właśnie wynik pochodnej czasowej wektora prędkości.

Teraz pozostały nam już tylko wyrażenia po prawej stronie znaku równości, które reprezentują wszystkie siły działające na płyn.
Pierwszy człon ∇p jest gradientem ciśnienia. Reprezentuje on różnicę ciśnień w przestrzeni, w której znajduje się płyn. Na przykład, jeśli istnieje strefa o niskim ciśnieniu i inna o wyższym ciśnieniu, płyn będzie się przemieszczał z części o wysokim ciśnieniu do niższej. Gradient p mówi o tym wszystkim.
Drugi człon opisuje lepkość płynu. Pomyśl o dwóch różnych cieczach, takich jak woda i miód. Kiedy nalewasz szklankę wody, spada ona szybko i łatwo. Kiedy zrobisz to samo z miodem, jest on lepki i leje się bardzo powoli. To właśnie mówi to wyrażenie.
Ostatni człon, F, jest najłatwiejszy, ponieważ reprezentuje on wszystkie siły zewnętrzne, które mogą być przyłożone do tego płynu. Zazwyczaj siłą, którą tu rozważamy jest grawitacja.
To jest to, wszystkie te wymyślne symbole i znaczenia literowe to po prostu siła = masa x przyspieszenie.
Użycie równań Naviera-Stokesa
Ponieważ rozwiązywanie tych równań jest tak skomplikowane, aby ich użyć musimy dokonać wielu przybliżeń. Niektóre przykłady to przepływ Poiseuille’a i Couette’a. Przy wielu założeniach, ci dwaj naukowcy byli w stanie znaleźć rozwiązanie równań Naviera-Stokesa dla bardzo specyficznego zastosowania. Jeśli jednak chcemy wykorzystać je do bardziej skomplikowanych zadań, takich jak prognozy pogody, musimy zrobić coś innego.
Najczęstszym sposobem wykorzystania tych równań jest ich przekształcenie, z wykorzystaniem średniej Reynoldsa. Jest to zaawansowany proces matematyczny, a jego wynikiem są równania Reynoldsa. Są one zwykle nazywane równaniami RANS (co oznacza uśrednione przez Reynoldsa równania Naviera-Stokesa).
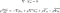
Równania te są używane, gdy płyn znajduje się w przepływie turbulentnym. Wyglądają one prawie dokładnie tak samo jak równania Naviera-Stokesa, z wyjątkiem ostatniego członu. Jest to tzw. tensor naprężenia Reynoldsa. Jest to wielkość, która umożliwia nam uwzględnienie turbulencji w płynie.
W równaniach RANS wielkości, których używamy są uśredniane w przedziale czasu. Przedział ten musi być wystarczająco mały, aby umożliwić obserwację zjawiska, które badamy. Jednocześnie musi on być na tyle duży, aby efekt turbulencji stracił na znaczeniu.
Przy odpowiednich założeniach równania te działają. Wiemy, jak ich używać, aby bolidy F1 były szybsze, aby statek kosmiczny poleciał na ISS i aby zrobić prognozę pogody. Możecie się więc zastanawiać, dlaczego dowód tych równań jest wart milion dolarów?
Nagroda miliona dolarów
Z punktu widzenia fizyki te równania to po prostu drugie prawo Newtona, które działa z płynami. Kiedy przyjmiemy pewne założenia i pewne uproszczenia, możemy zrobić z nimi niesamowite rzeczy.
Prawdziwy problem jest taki. Rozwiązywanie tych równań bez przybliżeń jest po prostu strasznie skomplikowane. Jest to tak trudne, że nie udowodniono, że rozwiązania rzeczywiście istnieją. I tu właśnie pojawia się Nagroda Milenijna.
Oficjalny opis problemu (można go znaleźć tutaj) brzmi następująco:
Udowodnij lub podaj kontrprzykład następującego stwierdzenia: w trzech wymiarach przestrzennych i czasie, biorąc pod uwagę początkowe pole prędkości, istnieje wektor prędkości i skalarne pole ciśnienia, które są zarówno gładkie, jak i globalnie zdefiniowane, które rozwiązują równania Naviera-Stokesa.
Co to oznacza, że aby zdobyć nagrodę, musisz zrobić trzy rzeczy:
- udowodnić, że rozwiązanie istnieje
- Rozwiązanie musi istnieć w każdym punkcie przestrzeni
- Rozwiązanie musi być gładkie. Oznacza to, że niewielka zmiana w warunkach początkowych powoduje tylko niewielką zmianę wyniku.
Dla inżyniera zazwyczaj wystarczy wiedzieć, że te równania działają, nawet jeśli tylko na pewnym poziomie przybliżenia. Jednak dla matematyka jest bardzo ważne, aby wiedzieć, czy rozwiązania istnieją i jak się zachowują.
Możesz teraz pomyśleć, że jeśli działają tak, jak działają, to poświęcanie czasu i energii na szukanie dowodu jest całkowitą stratą czasu. Cóż, jak wiele technologicznych postępów w historii ludzkości, wynik może nie wydawać się bardzo ważny. To, co jest ważne, to droga do niego, która może przynieść nową wiedzę i ulepszenia w naszym życiu.
Pomyśl o misjach kosmicznych. Gdyby ludzie nigdy nie zdecydowali się pójść i chodzić po Księżycu, nie mielibyśmy wielu przedmiotów, które są używane do poprawy naszego życia. Aparaty MRI i rozruszniki serca pochodzą z technologii opracowanych na potrzeby eksploracji kosmosu. Dziś lekarze na całym świecie używają ich każdego dnia, aby ratować życie. Tak samo jest w tym przypadku. Droga do odkrycia rozwiązania równań Naviera-Stokesa pomoże nam poprawić nasze zrozumienie płynów i nie tylko. Może nas to doprowadzić do nowych odkryć i prawdopodobnie będzie wymagało wynalezienia nowej matematyki. Może to być następnie wykorzystane do odpowiedzi na wiele innych problemów, do wynalezienia nowych technologii, które poprawią nasze życie i uczynią nas lepszymi.