Construct Equilateral Triangle – MathBitsNotebook (Geo

Trójkąt równoboczny MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits’ Teacher Resources Terms of Use Osoba kontaktowa: Donna Roberts

Używaj tylko kompasu i prostej krawędzi podczas rysowania konstrukcji. Żadnego rysowania z wolnej ręki!

Będziemy wykonywać TRZY konstrukcje trójkąta równobocznego. Pierwsza z nich będzie polegała na skonstruowaniu trójkąta równobocznego na podstawie długości jednego boku, a dwie pozostałe będą polegały na skonstruowaniu trójkąta równobocznego wpisanego w okrąg.

Dane: długość jednego boku trójkąta Skonstruuj: trójkąt równoboczny

KROKI:
1. Umieść punkt kompasu na punkcie A i zmierz odległość do punktu B. Zamachnij się łukiem o tej wielkości nad (lub pod) odcinkiem.
2. Nie zmieniając rozpiętości na kompasie, umieść punkt kompasu na punkcie B i zamachnij się tym samym łukiem, przecinając się z pierwszym łukiem.
3. Oznacz punkt przecięcia jako trzeci wierzchołek trójkąta równobocznego.

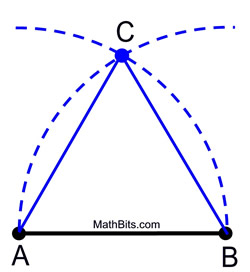Zobacz pełne okręgi w pracy.

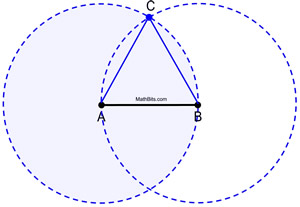Dowód konstrukcji: Okrąg A jest przystający do okręgu B, gdyż każdy z nich został utworzony przy użyciu tej samej długości promienia, AB. Skoro AB i AC są długościami promieni okręgu A, to są one sobie równe. Podobnie, AB i BC są promieniami okręgu B i są sobie równe. Zatem AB = AC = BC na zasadzie podstawienia (lub własności przechodniej). Ponieważ przystające odcinki mają równe długości, i ΔABC jest równoboczny (ma trzy przystające boki).

KROKI:
1. Umieść punkt kompasu na papierze i narysuj okrąg. (Zachowaj tę rozpiętość kompasu!)
2. Umieść kropkę, oznaczoną literą A, w dowolnym miejscu na obwodzie okręgu, aby służyła jako punkt początkowy.
3. Nie zmieniając rozpiętości na kompasie, umieść punkt kompasu na A i zataczaj mały łuk przecinający obwód koła.
4. Nie zmieniając rozpiętości na kompasie, przesuń punkt kompasu na przecięcie poprzedniego łuku z obwodem i zataczaj kolejny mały łuk na obwodzie koła.
5. Powtarzaj ten proces „kroczenia” po okręgu, aż wrócisz do punktu A.
6. Zaczynając od punktu A, połącz co drugi łuk na okręgu, aby utworzyć trójkąt równoboczny.

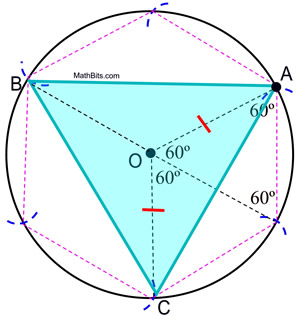Więcej informacji na temat dowodu tej konstrukcji można znaleźć w dowodzie na istnienie sześciokąta foremnego wpisanego.

Dowód konstrukcji: Z dowodu na sześciokąt foremny wpisany wynika, że kąty środkowe sześciokąta foremnego zawierają 60º. Kąty środkowe trójkąta wpisanego w ten okrąg zawierają 120º. Ponieważ ΔAOC jest równoramienny (OA i OC są długościami promieni), to m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA według SAS. Z CPCTC wynika, że ∠OCB ∠OCA i m∠OCB = 30º przez podstawienie oraz m∠BCA = 60º. W podobny sposób mamy m∠ACB = m∠CBA = m∠BAC = 60º oraz trójkąt równoboczny ΔABC.

KROKI:
1. Umieść punkt kompasu na papierze i narysuj okrąg, O. (Zachowaj tę rozpiętość kompasu!)
2. Używając linijki prostej, narysuj średnicę okręgu, oznaczając punkty końcowe P i B.
3. Nie zmieniając rozpiętości na kompasie, umieść punkt kompasu na P i narysuj pełny okrąg.
4. Oznacz punkty przecięcia obu obwodów okręgu literami A i C.
5. Narysuj odcinki z A do B, z B do C i z C do A, aby utworzyć trójkąt równoboczny.

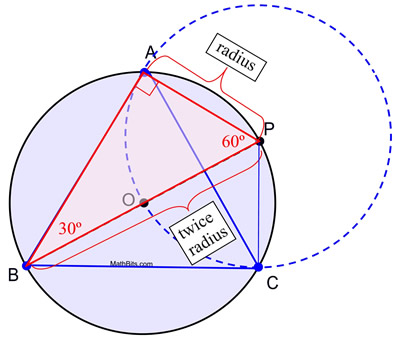
Dowód konstrukcji: Konstrukcja ta wykorzystuje fakt, że kąt wpisany w półkole jest kątem prostym, oraz że w trójkącie 30º-60º-90º długość krótszej nogi jest połową długości przeciwprostokątnej. W tej konstrukcji okręgi O i P są przystające, ponieważ ich promienie mają taką samą długość. AP jest długością promienia okręgu P, a promień AP = OP. OP jest także długością promienia okręgu O (wraz z OB), a średnica BP = BO + OP = 2 OP. Podstawiając, BP = 2 AP, tworzymy warunki konieczne, aby m∠ABP = 30º. W związku z tym m∠APB = 60º. Podobny argument można zastosować do ustalenia, że dla ΔPBC, m∠PBC = 30º i m∠BPC = 60º, co czyni ΔPBC ΔPBA przez ASA (ze wspólnym bokiem od B do P).
Teraz, ponieważ są to odpowiednie boki dwóch przystających trójkątów, co czyni ΔABC równoramiennym. ∠BAC ∠BCA, ponieważ kąty podstawy trójkąta równoramiennego są przystające.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º z postulatu dodawania kątów i podstawiania. m∠BAC + m∠BCA + m∠ABC = 180º, ponieważ suma miar kątów w trójkącie wynosi 180º. Ponieważ m∠BAC + m∠BAC + 60º = 180º przez podstawienie, wiemy, że 2m∠BAC = 120º i m∠BAC = 60º. W związku z tym m∠BCA również równa się 60º przez podstawienie, co czyni ΔABC równoboczną.

.