Co to jest przepuszczalność błony komórkowej?
Tryb czytelnika
Jedną z charakterystycznych cech wszystkich organizmów żywych jest to, że zawierają one charakterystyczną mieszaninę jonów i małych cząsteczek. Skład ten nie tylko różni się od środowiska, ale może również zmieniać się w obrębie komórki. Na przykład, stężenie jonów wodorowych w niektórych przedziałach komórkowych może być 104 razy większe niż w innych (mitochondria osiągające pH tak wysokie jak 8; lizosomy z pH tak niskim jak 4, BNID 107521, 106074). Stosunek stężeń jonów Ca2+ w przedziałach płynu zewnątrz- i wewnątrzkomórkowego może być ponownie 104-krotny (BNID 104083). Ta różnica stężeń jest tak duża, że transport jonu Ca2+ przez błonę, z przedziału wewnątrz- do zewnątrzkomórkowego, wymaga energii więcej niż jednego protonu lub jonu sodowego spływającego po gradiencie siły protonomotorycznej. Aby się o tym przekonać, czytelnik powinien przypomnieć sobie zasadę z naszej listy sztuczek handlowych, że do ustalenia różnicy potencjałów rzędu wielkości potrzeba 6 kJ/mol (≈2 kBT). Taką energię można uzyskać na przykład poprzez transport jednego ładunku elektrycznego przez różnicę potencjałów 60 mV. Aby osiągnąć cztery rzędy wielkości stosunku koncentracji, ładunek musiałby przebyć drogę około 240 mV siły napędowej elektronów (w rzeczywistości nawet więcej ze względu na podwójny ładunek jonu wapnia). Jest to bardzo blisko napięcia załamania membrany, jak to zostało omówione w winiecie na temat „Czym jest różnica potencjałów elektrycznych w membranach?”. Rzeczywiście wysoki stosunek stężenia Ca2+ jest zwykle osiągany przez sprzężenie z transportem trzech jonów sodu lub hydrolizą ATP, co pomaga osiągnąć wymaganą różnicę gęstości bez niebezpiecznego energetyzowania błony.
Drugie prawo termodynamiki uczy nas, że, ogólnie rzecz biorąc, obecność gradientów stężenia zostanie ostatecznie usunięta przez procesy transportu masy, które stale prowadzą systemy do stanu równowagi. Jednakże, chociaż drugie prawo termodynamiki mówi nam o charakterze ostatecznego stanu systemu (np. jednolite stężenia), nie mówi nam, jak długo potrwa osiągnięcie tego stanu. Membrany ewoluowały, tworząc bardzo skuteczną barierę dla spontanicznego przenoszenia wielu gatunków jonowych i molekularnych. Aby oszacować skalę czasową wyrównywania stężeń, musimy znać szybkość transportu masy, która zależy od kluczowych właściwości materiału, takich jak stałe dyfuzji i przepuszczalności.
Niezwykle udaną klasą „praw”, które opisują zachowanie systemów, które doznały jakiegoś niewielkiego odstępstwa od równowagi, są liniowe prawa transportu. Prawa te zakładają prostą liniową zależność pomiędzy szybkością transportu jakiejś interesującej nas wielkości a związaną z nią siłą napędową. W przypadku transportu masy, istnieje liniowa zależność pomiędzy strumieniem (tj. liczbą cząsteczek przekraczających jednostkę powierzchni w jednostce czasu) a różnicą stężeń (która służy jako odpowiednia siła napędowa). W przypadku transportu przez membrany, idee te zostały skodyfikowane w prostym równaniu (dla neutralnego solutu) j= – p-(cin-cout), gdzie j jest strumieniem netto do komórki, cin i cout odnoszą się do stężeń wewnątrz i na zewnątrz regionu związanego z membraną, a p jest parametrem materiałowym znanym jako przepuszczalność. Jednostki p można wydedukować zauważając, że strumień ma jednostki liczba/(powierzchnia x czas), a stężenie ma jednostki liczba/objętość, co sugeruje, że jednostkami p są długość/czas. Podobnie jak wiele wielkości transportowych (np. przewodnictwo elektryczne materiałów, które obejmuje ponad 30 rzędów wielkości), przepuszczalność ma bardzo duży zakres dynamiczny, jak pokazano na Rysunku 1. Jak widać na rysunku, dwuwarstwy lipidowe mają prawie 1010-krotny zakres przepuszczalności.
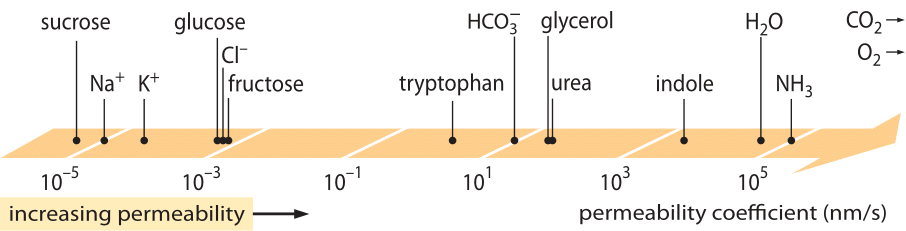
Rysunek 1: Szeroki zakres przepuszczalności błon dla różnych związków w komórce. Membrany są bardziej przepuszczalne dla związków nienaładowanych i najmniej przepuszczalne dla jonów naładowanych. Zauważ, że istnienie kanałów jonowych spowoduje, że pozorna przepuszczalność, gdy są one otwarte, będzie o kilka rzędów wielkości wyższa. Jednostki zostały wybrane jako nm/s, a kilka nm to charakterystyczna szerokość membrany. Rysunek zaadaptowany z R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. Wartość dla glukozy jest mniejsza niż w Robertsonie na podstawie kilku źródeł, takich jak BNID 110830, 110807. Inne źródła danych: BNID 110729, 110731, 110816, 110824, 110806.
Jakie parametry fizyko-chemiczne kierują umiejscowieniem związku na tej skali przepuszczalności? Jedną z zasad jest to, że małe cząsteczki mają wyższą przepuszczalność niż większe cząsteczki. Inna zasada mówi, że związki neutralne mogą przekraczać błonę o wiele rzędów wielkości szybciej niż podobne związki naładowane. Wśród związków naładowanych, związki ujemne (anionowe) mają tendencję do posiadania znacznie wyższej przepuszczalności niż związki dodatnie (kationowe). Tak zwana reguła Overtona mówi, że przepuszczalność membrany wzrasta wraz z hydrofobowością, gdzie hydrofobowość jest tendencją związku do preferowania niepolarnego rozpuszczalnika w stosunku do rozpuszczalnika polarnego (wodnego). Reguła Overtona przewiduje, że naładowane cząsteczki (niehydrofobowe), takie jak jony, będą miały tendencję do niskiej przepuszczalności, ponieważ ponoszą karę energetyczną związaną z przenikaniem przez membranę, podczas gdy rozpuszczone gazy, takie jak O2 i CO2, które są hydrofobowe (ponieważ są nienaładowane i symetryczne), będą miały wysoką przepuszczalność. Rzeczywiście, przepuszczalność błon dwuwarstwowych lipidów dla CO2 daje wartości, które wynoszą 0.01-1 cm/s (tak, pomiary przepuszczalności mają bardzo wysoką niepewność w różnych laboratoriach, BNID 110004, 110617, 102624), wyższe niż wszystkie inne wartości pokazane na Rysunku 1. Wartość ta pokazuje, że bariera stworzona przez błonę komórkową jest w rzeczywistości mniejszą przeszkodą niż bariera spowodowana przez niewzburzoną warstwę wody pochłaniającą błonę komórkową od zewnątrz. Takie wnioskowanie można wyprowadzić z równania na współczynnik przepuszczalności przeszkody, dany przez p=K x D/l, gdzie l jest szerokością, D współczynnikiem dyfuzji, a K współczynnikiem podziału pomiędzy medium a materiałem przeszkody. Jest to również znane jako model „rozpuszczalność-dyfuzja” dla przepuszczalności, gdzie oznaczają one efekty K i D, które są dwoma etapami wpływającymi na przepuszczalność. Dla niezakłóconej warstwy wody K=1, ponieważ jest ona bardzo podobna do mediów, ale dla membran wartość ta dla wszystkich, z wyjątkiem najbardziej hydrofobowych materiałów, jest zwykle o kilka rzędów wielkości mniejsza niż 1. Ta zależność od K jest podstawą wspomnianej wyżej reguły Overtona. Wysoka przepuszczalno¶ć dla CO2 sugeruje również, że kanały takie jak akwaporyny, które sugerowano, że służ± do transportu gazu do komórki, nie s± potrzebne, ponieważ błona jest wystarczaj±co przepuszczalna. Aby zobaczyć, jak właściwości błony wpływają na chemiczny skład metabolitów, przechodzimy do obliczania czasu wycieku dla różnych związków
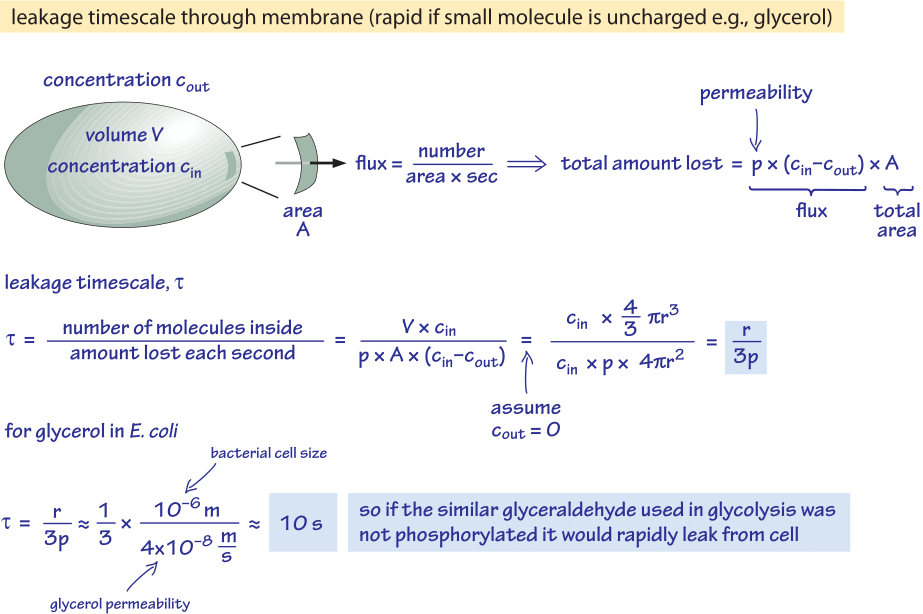
Rysunek 2: Obliczenia wsteczne skali czasu dla niefosforylowanej cząsteczki glukozy do pasywnej dyfuzji z komórki bakteryjnej. Implikacje funkcjonalne są następnie rozważane dla szybko rosnącej komórki, gdzie efekt ten jest pomijalny i dla komórek w stanie stacjonarnym, gdzie może powodować znaczny wyciek zasobów.
Rozważamy na przykład glicerol. Analiza przedstawiona na rysunku 2 daje szacunkowy czas jego wycieku z komórki, jeśli cząsteczka nie jest fosforylowana lub w inny sposób przekształcana w formę bardziej hydrofilową. Przepuszczalność błony komórkowej dla glicerolu wynosi p≈10-100 nm/s (BNID 110824), jak można odczytać z rysunku 1. Skala czasu, w którym cząsteczka glicerolu wewnątrz komórki ucieka z powrotem do otaczającego ją medium, przy założeniu braku przepływu zwrotnego do komórki (cout=0), może być zgrubnie oszacowana poprzez zauważenie, że wypływ z komórki wynosi p-A-cin, gdzie A jest powierzchnią komórki. Skala czasowa jest znaleziona poprzez wzięcie całkowitej ilości w komórce, V-cin (gdzie V jest objętością komórki lub dokładniej objętością wody w komórce), i podzielenie przez ten strumień, co daje dla komórki bakteryjnej (r≈1 μm) w skali czasowej:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Jest to przybliżone oszacowanie, ponieważ nie uwzględniliśmy malejącego stężenia cin z czasem, co da współczynnik korekcji 1/ln(2), czyli mniej niż 2-krotny wzrost. Z tych szacunków dowiadujemy się, że jeśli glikolityczne produkty pośrednie gliceraldehyd lub dihydroksyaceton, które są bardzo podobne do glicerolu, nie byłyby fosforylowane, co skutkowałoby dodaniem ładunku, zostałyby utracone do medium przez dyfuzję przez błonę komórkową. W pożywkach laboratoryjnych, gdzie źródło węgla jest dostarczane w obfitości, nie stanowi to większego problemu, ale w środowisku naturalnym, gdzie komórki często czekają w fazie stacjonarnej na szczęśliwy impuls składników odżywczych (uważa się, że E. coli uważa się, że po wydaleniu z organizmu może miesiącami nie rosnąć, zanim znajdzie nowego gospodarza), komórka może ograniczyć swoje straty, upewniając się, że półprodukty metaboliczne są znakowane ładunkiem, który uniemożliwi im ponowne przekroczenie bariery prezentowanej przez warstwę lipidową.





.