Wprowadzenie
Wyobraź to sobie – Zostałeś poproszony o prognozowanie ceny następnego iPhone’a i otrzymałeś dane historyczne. Obejmują one takie cechy, jak kwartalna sprzedaż, wydatki miesiąc do miesiąca i cały szereg rzeczy, które pochodzą z bilansu Apple. Jako data scientist, jaki rodzaj problemu sklasyfikowałbyś to jako? Modelowanie szeregów czasowych, oczywiście.
Od przewidywania sprzedaży produktu do szacowania zużycia energii elektrycznej w gospodarstwach domowych, prognozowanie szeregów czasowych jest jedną z podstawowych umiejętności, które każdy naukowiec zajmujący się danymi powinien znać, jeśli nie opanować. Istnieje wiele różnych technik, z których można korzystać, a w tym artykule zajmiemy się jedną z najbardziej efektywnych, zwaną Auto ARIMA.

Najpierw zrozumiemy koncepcję ARIMA, która doprowadzi nas do naszego głównego tematu – Auto ARIMA. Aby ugruntować nasze pojęcia, zajmiemy się zbiorem danych i zaimplementujemy go zarówno w Pythonie, jak i w R.
Table of content
- Co to jest szereg czasowy?
- Metody prognozowania szeregów czasowych
- Wprowadzenie do ARIMA
- Kroki implementacji ARIMA
- Dlaczego potrzebujemy Auto ARIMA?
- Implementacja auto ARIMA (na zbiorze danych pasażerów samolotów)
- Jak auto ARIMA dobiera parametry?
Jeśli jesteś zaznajomiony z szeregami czasowymi i ich technikami (takimi jak średnia ruchoma, wygładzanie wykładnicze i ARIMA), możesz przejść bezpośrednio do sekcji 4. Dla początkujących, zacznij od poniższej sekcji, która jest krótkim wprowadzeniem do szeregów czasowych i różnych technik prognozowania.
Co to jest szereg czasowy?
Zanim poznamy techniki pracy na danych szeregów czasowych, musimy najpierw zrozumieć, czym właściwie jest szereg czasowy i jak różni się od każdego innego rodzaju danych. Oto formalna definicja szeregu czasowego – Jest to seria punktów danych mierzonych w stałych odstępach czasu. Oznacza to po prostu, że poszczególne wartości są rejestrowane w stałym odstępie czasu, które mogą być godzinne, dzienne, tygodniowe, co 10 dni, i tak dalej. To, co odróżnia serie czasowe od siebie, to fakt, że każdy punkt danych w serii jest zależny od poprzednich punktów danych. Zrozummy różnicę wyraźniej, biorąc kilka przykładów.
Przykład 1:
Załóżmy, że masz zbiór danych osób, które wzięły pożyczkę od konkretnej firmy (jak pokazano w poniższej tabeli). Czy uważasz, że każdy wiersz będzie powiązany z poprzednimi wierszami? Z pewnością nie! Pożyczka zaciągnięta przez daną osobę będzie oparta na jej warunkach finansowych i potrzebach (mogą istnieć inne czynniki, takie jak wielkość rodziny itp., ale dla uproszczenia rozważamy tylko dochód i rodzaj pożyczki). Ponadto, dane nie były zbierane w żadnym określonym przedziale czasowym. Zależy to od tego, kiedy firma otrzymała wniosek o pożyczkę.

Przykład 2:
Przyjrzyjrzyjmy się innemu przykładowi. Załóżmy, że masz zbiór danych, który zawiera poziom CO2 w powietrzu na dzień (zrzut ekranu poniżej). Czy będziesz w stanie przewidzieć przybliżoną ilość CO2 na następny dzień, patrząc na wartości z ostatnich kilku dni? No cóż, oczywiście. Jeśli zauważysz, że dane zostały zarejestrowane codziennie, czyli przedział czasowy jest stały (24 godziny).

Musisz mieć już intuicję na ten temat – pierwszy przypadek to prosty problem regresji, a drugi to problem szeregów czasowych. Chociaż zagadka szeregów czasowych może być również rozwiązana za pomocą regresji liniowej, ale to nie jest najlepsze podejście, ponieważ zaniedbuje związek wartości ze wszystkimi względnymi wartościami z przeszłości. Spójrzmy teraz na niektóre z powszechnych technik stosowanych do rozwiązywania problemów związanych z szeregami czasowymi.
Metody prognozowania szeregów czasowych
Istnieje wiele metod prognozowania szeregów czasowych i pokrótce omówimy je w tej sekcji. Szczegółowe wyjaśnienia i kody Pythona dla wszystkich poniższych technik można znaleźć w tym artykule: 7 technik prognozowania szeregów czasowych (z kodami python).
- Podejście naiwne: W tej technice prognozowania, wartość nowego punktu danych jest przewidywana jako równa poprzedniemu punktowi danych. Rezultatem będzie płaska linia, ponieważ wszystkie nowe wartości przyjmują poprzednie wartości.
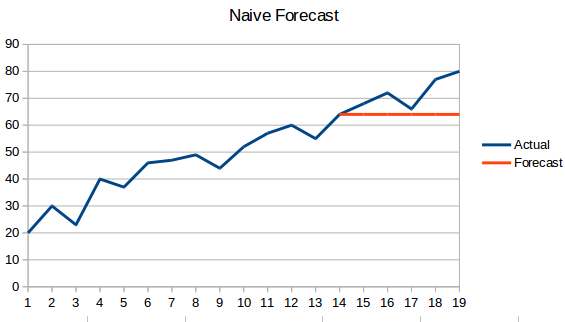
- Średnia prosta: Następna wartość jest brana jako średnia wszystkich poprzednich wartości. Przewidywania tutaj są lepsze niż „Naive Approach”, ponieważ nie powoduje płaskiej linii, ale tutaj wszystkie wartości w przeszłości są brane pod uwagę, co nie zawsze może być przydatne. Na przykład, gdy poproszony, aby przewidzieć dzisiejszą temperaturę, należy rozważyć ostatnie 7 dni „temperatura, a nie temperatura miesiąc temu.

- Średnia krocząca: Jest to poprawa w stosunku do poprzedniej techniki. Zamiast brać średnią wszystkich poprzednich punktów, średnia 'n’ poprzednich punktów jest brana jako przewidywana wartość.

- Średnia ruchoma ważona : Średnia ruchoma ważona jest średnią ruchomą, gdzie przeszłe 'n’ wartości mają różne wagi.

- Simple Exponential Smoothing: W tej technice większe wagi przypisuje się bardziej niedawnym obserwacjom niż obserwacjom z odległej przeszłości.

- Holt’s Linear Trend Model: W metodzie tej uwzględnia się trend zbioru danych. Przez trend rozumiemy rosnący lub malejący charakter serii. Załóżmy, że liczba rezerwacji w hotelu wzrasta każdego roku, wtedy możemy powiedzieć, że liczba rezerwacji wykazuje trend rosnący. Funkcja prognozy w tej metodzie jest funkcją poziomu i trendu.

- Metoda Holta Wintersa: Algorytm ten uwzględnia zarówno trend, jak i sezonowość szeregu. Na przykład – liczba rezerwacji w hotelu jest wysoka w weekendy & niska w dni powszednie, i wzrasta każdego roku; istnieje sezonowość tygodniowa i trend rosnący.

- ARIMA: ARIMA jest bardzo popularną techniką modelowania szeregów czasowych. Opisuje ona korelację pomiędzy punktami danych i uwzględnia różnicę wartości. Udoskonaleniem ARIMA jest SARIMA (lub sezonowa ARIMA). Przyjrzymy się ARIMA nieco bardziej szczegółowo w następnej sekcji.
Wprowadzenie do ARIMA
W tej sekcji zrobimy szybkie wprowadzenie do ARIMA, które będzie pomocne w zrozumieniu Auto Arima. Szczegółowe wyjaśnienie Arimy, parametrów (p,q,d), wykresów (ACF PACF) i implementacji jest zawarte w tym artykule: Complete tutorial to Time Series.
ARIMA jest bardzo popularną metodą statystyczną służącą do prognozowania szeregów czasowych. ARIMA to skrót od Auto-Regressive Integrated Moving Averages. Modele ARIMA działają w oparciu o następujące założenia –
- Seria danych jest stacjonarna, co oznacza, że średnia i wariancja nie powinny zmieniać się w czasie. Szereg można uczynić stacjonarnym poprzez zastosowanie transformacji logicznej lub różnicowanie szeregu.
- Dane dostarczone jako dane wejściowe muszą być szeregiem jednozmiennym, ponieważ arima wykorzystuje wartości przeszłe do przewidywania wartości przyszłych.
ARIMA ma trzy komponenty – AR (termin autoregresyjny), I (termin różnicujący) i MA (termin średniej ruchomej). Zrozummy każdy z tych komponentów –
- Termin AR odnosi się do przeszłych wartości używanych do prognozowania następnej wartości. Termin AR jest definiowany przez parametr 'p’ w arimie. Wartość 'p’ jest określana za pomocą wykresu PACF.
- TerminMA jest używany do określenia liczby przeszłych błędów prognozy używanych do przewidywania przyszłych wartości. Parametr „q” w arimie reprezentuje termin MA. ACF plot jest używany do identyfikacji prawidłowej wartości 'q’.
- Rozdzielczość różnicowania określa liczbę razy operacja różnicowania jest wykonywana na serii, aby uczynić ją stacjonarną. Testy takie jak ADF i KPSS mogą być użyte do określenia, czy szereg jest stacjonarny i pomóc w identyfikacji wartości d.
Kroki implementacji modelu ARIMA
Ogólne kroki implementacji modelu ARIMA są następujące –
- Załaduj dane: Pierwszym krokiem do budowy modelu jest oczywiście załadowanie zbioru danych
- Preprocessing: W zależności od zbioru danych zostaną zdefiniowane kroki wstępnego przetwarzania. Obejmować to będzie tworzenie znaczników czasu, konwersję typu dtype kolumny data/czas, uczynienie szeregu jednozmiennowym, itp.
- Uczynienie szeregu stacjonarnym: Aby spełnić założenie, konieczne jest uczynienie szeregu stacjonarnym. Obejmuje to sprawdzenie stacjonarności szeregu i wykonanie wymaganych przekształceń
- Określenie wartości d: Dla uczynienia serii stacjonarną, liczba razy operacja różnicy została wykonana zostanie przyjęta jako wartość d
- Tworzenie wykresów ACF i PACF: Jest to najważniejszy krok w implementacji ARIMA. Działki ACF PACF są używane do określenia parametrów wejściowych dla naszego modelu ARIMA
- Wyznacz wartości p i q: Odczytaj wartości p i q z wykresów w poprzednim kroku
- Fit ARIMA model: Używając przetworzonych danych i wartości parametrów, które obliczyliśmy z poprzednich kroków, dopasuj model ARIMA
- Predict values on validation set: Przewiduj przyszłe wartości
- Oblicz RMSE: Aby sprawdzić wydajność modelu, sprawdź wartość RMSE, używając przewidywań i rzeczywistych wartości na zbiorze walidacyjnym
Dlaczego potrzebujemy Auto ARIMA?
Ale ARIMA jest bardzo potężnym modelem do prognozowania danych szeregów czasowych, procesy przygotowania danych i dostrajania parametrów są naprawdę czasochłonne. Przed zaimplementowaniem modelu ARIMA, należy nadać szeregowi stacjonarność oraz określić wartości p i q za pomocą wykresów, które omówiliśmy powyżej. Auto ARIMA bardzo ułatwia nam to zadanie, ponieważ eliminuje kroki od 3 do 6, które widzieliśmy w poprzedniej sekcji. Poniżej znajdują się kroki, które należy wykonać, aby zaimplementować auto ARIMA:
- Załaduj dane: Ten krok będzie taki sam. Załaduj dane do swojego notatnika
- Preprocessing data: Dane wejściowe powinny być jednowariantowe, stąd opuść pozostałe kolumny
- Fit Auto ARIMA: Dopasuj model na szeregu jednowariantowym
- Predict values on validation set: Make predictions on the validation set
- Calculate RMSE: Check the performance of the model using the predicted values against the actual values
Zupełnie ominęliśmy wybór cech p i q, jak widać. Co za ulga! W następnej sekcji zaimplementujemy auto ARIMA przy użyciu zabawkowego zbioru danych.
Implementacja w Pythonie i R
Będziemy używać zbioru danych International-Air-Passenger. Ten zbiór danych zawiera miesięczną sumę liczby pasażerów (w tysiącach). Ma dwie kolumny – miesiąc i liczba pasażerów. Zbiór danych można pobrać z tego linku.
#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)
output -76.51355764316357
Poniżej znajduje się kod R dla tego samego problemu:
# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)
Jak Auto Arima wybiera najlepsze parametry
W powyższym kodzie użyliśmy po prostu polecenia .fit(), aby dopasować model bez konieczności wybierania kombinacji p, q, d. Ale jak model wybrał najlepszą kombinację tych parametrów? Auto ARIMA bierze pod uwagę wartości AIC i BIC wygenerowane (jak widać w kodzie), aby określić najlepszą kombinację parametrów. Wartości AIC (Akaike Information Criterion) i BIC (Bayesian Information Criterion) są estymatorami służącymi do porównywania modeli. Im niższe są te wartości, tym lepszy jest model.
Sprawdź te linki, jeśli jesteś zainteresowany matematyką stojącą za AIC i BIC.
Uwagi końcowe i dalsze lektury
Znalazłem auto ARIMA jako najprostszą technikę do wykonywania prognozowania szeregów czasowych. Znajomość skrótu jest dobra, ale bycie zaznajomionym z matematyką stojącą za nim jest również ważne. W tym artykule prześlizgnąłem się po szczegółach, jak działa ARIMA, ale upewnij się, że przejdziesz przez linki podane w artykule. Dla łatwego odniesienia, oto linki ponownie:
- Wyczerpujący przewodnik dla początkujących do prognozowania szeregów czasowych w Pythonie
- Kompletny samouczek do szeregów czasowych w R
- 7 technik prognozowania szeregów czasowych (z kodami Pythona)
Sugerowałbym przećwiczenie tego, czego nauczyliśmy się tutaj na tym problemie praktycznym: Time Series Practice Problem. Możesz również wziąć udział w naszym kursie szkoleniowym stworzonym na tym samym problemie praktycznym, Prognozowanie szeregów czasowych, aby zapewnić sobie dobry start.