Opiszemy trzy przykłady z nauk przyrodniczych: jeden z fizyki, jeden związany z genetyką i jeden z eksperymentu na myszach. Są one bardzo różne, ale w końcu używamy tej samej techniki statystycznej: dopasowania modeli liniowych. Modele liniowe są zazwyczaj nauczane i opisywane w języku algebry macierzowej.
Motywujące przykłady
Spadające obiekty
Wyobraź sobie, że jesteś Galileuszem w XVI wieku, który próbuje opisać prędkość spadającego obiektu. Asystent wspina się na Wieżę w Pizie i upuszcza piłkę, podczas gdy kilku innych asystentów rejestruje jej położenie w różnym czasie.
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersAsystenci przekazują dane Galileuszowi i oto co on widzi:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")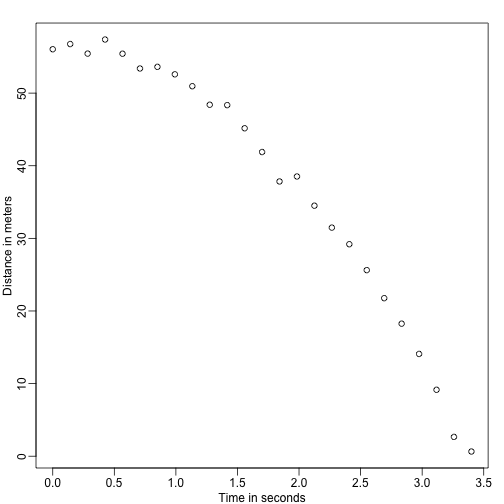
Nie zna dokładnego równania, ale patrząc na powyższy wykres wnioskuje, że położenie powinno być zgodne z parabolą. Więc modeluje dane za pomocą:
With reprezentującego położenie, reprezentującego czas i uwzględniającego błąd pomiaru. Jest to model liniowy, ponieważ stanowi liniową kombinację znanych wielkości (th s) określanych jako predyktory lub kowarianty oraz nieznanych parametrów (the s).
Wysokości ojca &syna
Wyobraź sobie, że jesteś Francisem Galtonem w XIX wieku i zbierasz sparowane dane dotyczące wzrostu od ojców i synów. Podejrzewasz, że wzrost jest dziedziczny. Twoje dane:
library(UsingR)x=father.son$fheighty=father.son$sheightwyglądają tak:
plot(x,y,xlab="Father's height",ylab="Son's height")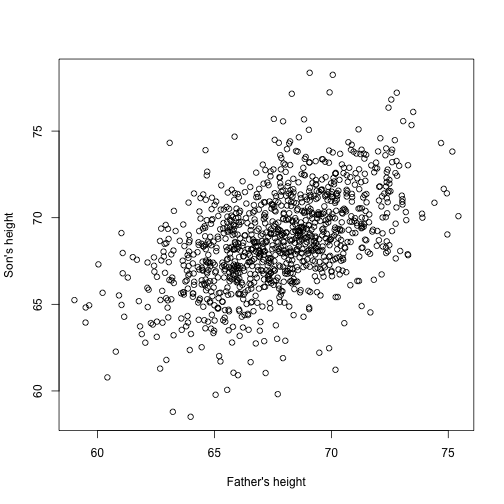
Wysokość synów wydaje się wzrastać liniowo wraz z wysokością ojców. W tym przypadku model, który opisuje dane, jest następujący:
Jest to również model liniowy z i , wysokościami ojca i syna odpowiednio dla -tej pary, oraz z członem uwzględniającym dodatkową zmienność. Tutaj myślimy o wysokościach ojców jako o predyktorach, które są stałe (nie losowe), więc używamy małych liter. Sam błąd pomiaru nie może wyjaśnić całej zmienności obserwowanej w . Ma to sens, ponieważ istnieją inne zmienne, których nie ma w modelu, na przykład wysokość matek, losowość genetyczna i czynniki środowiskowe.
Próby losowe z wielu populacji
Tutaj wczytujemy dane dotyczące masy ciała myszy, które były karmione dwiema różnymi dietami: wysokotłuszczową i kontrolną (chow). Mamy losową próbkę 12 myszy dla każdej z nich. Jesteśmy zainteresowani ustaleniem, czy dieta ma wpływ na wagę. Oto dane:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")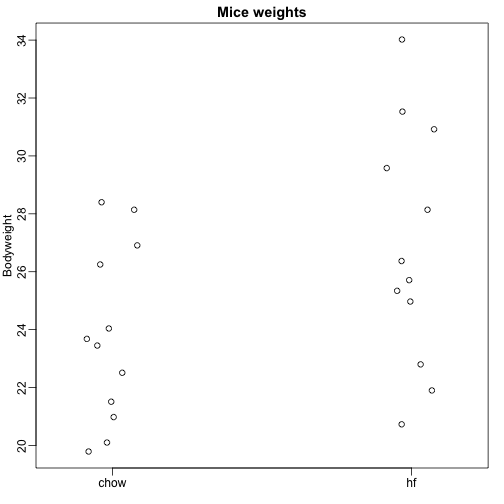
Chcemy oszacować różnicę w średniej wadze między populacjami. Pokazaliśmy, jak to zrobić za pomocą testów t i przedziałów ufności, bazując na różnicy średnich z próby. Możemy uzyskać te same dokładne wyniki za pomocą modelu liniowego:
ze średnią wagą w diecie chow, różnicą między średnimi, kiedy mysz dostaje dietę wysokotłuszczową (hf), kiedy dostaje dietę chow, i wyjaśnia różnice między myszami z tej samej populacji.
Modele liniowe w ogólności
Widzieliśmy trzy bardzo różne przykłady, w których można zastosować modele liniowe. Ogólny model, który obejmuje wszystkie powyższe przykłady, jest następujący:
Zauważ, że mamy ogólną liczbę predyktorów . Algebra macierzy zapewnia zwarty język i ramy matematyczne do obliczeń i pochodnych z dowolnego modelu liniowego, które pasują do powyższych ram.
Oszacowanie parametrów
Aby powyższe modele były użyteczne, musimy oszacować nieznane s. W pierwszym przykładzie chcemy opisać proces fizyczny, dla którego nie możemy mieć nieznanych parametrów. W drugim przykładzie, lepiej rozumiemy dziedziczenie poprzez oszacowanie jak bardzo, średnio, wzrost ojca wpływa na wzrost syna. W ostatnim przykładzie chcemy ustalić, czy faktycznie istnieje różnica: jeśli .
Standardowym podejściem w nauce jest znalezienie wartości, które minimalizują odległość dopasowanego modelu do danych. Poniższe równanie nazywamy równaniem najmniejszych kwadratów (LS) i będziemy się z nim często spotykać w tym rozdziale:
Po znalezieniu minimum będziemy nazywać wartości oszacowaniami najmniejszych kwadratów (LSE) i oznaczać je symbolem . Wielkość otrzymaną po obliczeniu równania najmniejszych kwadratów na oszacowaniach nazywamy resztową sumą kwadratów (RSS). Ponieważ wszystkie te wielkości zależą od , są one zmiennymi losowymi. The s are random variables and we will eventually perform inference on them.
Falling object example revisited
Dzięki mojemu nauczycielowi fizyki z liceum wiem, że równanie trajektorii spadającego obiektu jest następujące:
z i odpowiednio wysokością początkową i prędkością. Dane, które symulowaliśmy powyżej, podążały za tym równaniem i dodawały błąd pomiaru, aby symulować n obserwacje dla upuszczenia piłki z wieży w Pizie . Dlatego użyliśmy tego kodu do symulacji danych:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Oto jak wyglądają dane z linią ciągłą reprezentującą prawdziwą trajektorię:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)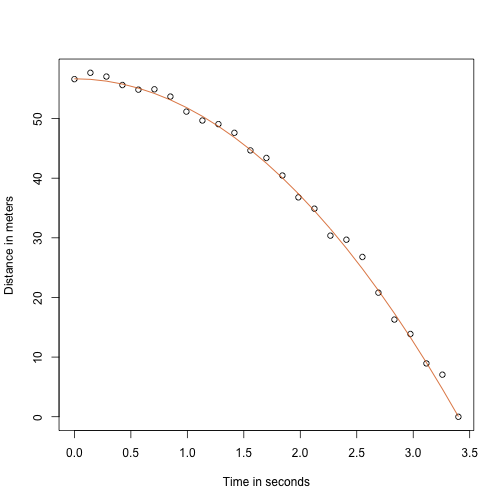
Ale udawaliśmy Galileusza, więc nie znamy parametrów modelu. Dane sugerują, że jest to parabola, więc modelujemy ją jako taką:
Jak znaleźć LSE?
Funkcja lm
W R możemy dopasować ten model po prostu używając funkcji lm. Opiszemy tę funkcję szczegółowo później, ale tutaj jest jej podgląd:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Daje nam ona LSE, jak również błędy standardowe i wartości p.
Częścią tego, co robimy w tej sekcji jest wyjaśnienie matematyki stojącej za tą funkcją.
Oszacowanie najmniejszych kwadratów (LSE)
Zapiszmy funkcję, która oblicza RSS dla dowolnego wektora :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Więc dla dowolnego trójwymiarowego wektora otrzymujemy RSS. Oto wykres RSS jako funkcji, gdy utrzymujemy dwie pozostałe stałe wartości:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)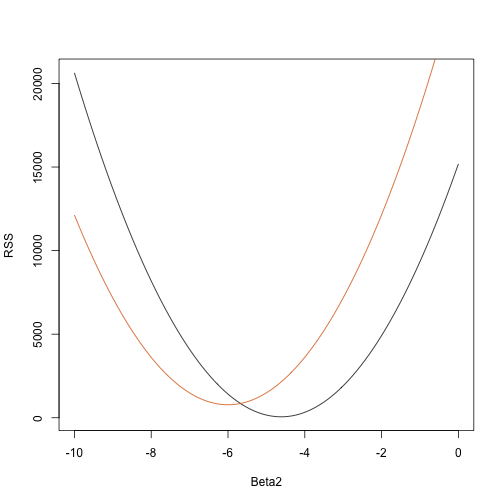
Próba i błąd tutaj nie zadziała. Zamiast tego możemy użyć rachunku: wziąć pochodne cząstkowe, ustawić je na 0 i rozwiązać. Oczywiście, jeśli mamy wiele parametrów, te równania mogą stać się dość skomplikowane. Algebra liniowa zapewnia zwarty i ogólny sposób rozwiązania tego problemu.
Więcej o Galtonie (Zaawansowane)
Podczas badania danych dotyczących ojca i syna, Galton dokonał fascynującego odkrycia, używając analizy eksploracyjnej.
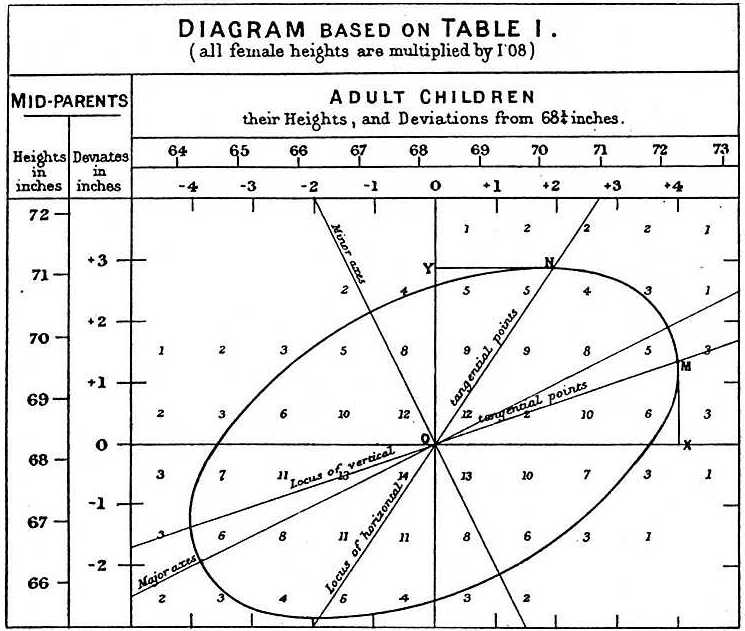
Zauważył, że jeśli zestawi w tabeli liczbę par wzrostu ojciec-syn i prześledzi wszystkie wartości x,y mające te same sumy w tabeli, utworzą one elipsę. Na powyższym wykresie, wykonanym przez Galtona, widać elipsę utworzoną przez pary mające 3 przypadki. To następnie doprowadziło do modelowania tych danych jako skorelowanych dwuczynnikowych normalnych, które opisaliśmy wcześniej:
Opisaliśmy, jak możemy użyć matematyki, aby pokazać, że jeśli utrzymasz stałą (warunek, aby być ) dystrybucja jest normalnie rozłożona ze średnią: i odchyleniem standardowym . Zauważmy, że jest to korelacja między i , co implikuje, że jeśli ustalimy , to w istocie podąża za modelem liniowym. Parametry i w naszym prostym modelu liniowym mogą być wyrażone za pomocą , i .
.