Możemy użyć równania Gibbsa-Helmholtza, aby uzyskać zależność temperaturową \(K)
}{∂T} \prawda)_P = \dfrac{-Δ_rH^o}{T^2}]
W stanie równowagi możemy zrównać \(Δ_rG^o\) z \(-RT^ln K\), więc otrzymujemy:
}{∂T} \_P = \dfrac{Δ_rH^o}{RT^2}
Widzimy, że to czy ∗ wzrasta czy maleje wraz z temperaturą jest związane z tym czy entalpia reakcji jest dodatnia czy ujemna. Jeżeli temperatura zmienia się na tyle nieznacznie, że Δ_rH^o można uznać za stałą, możemy przełożyć wartość Δ(K) w jednej temperaturze na inną, całkując powyższe wyrażenie, otrzymamy podobne wyprowadzenie, jak w przypadku obniżenia temperatury topnienia:
Jeżeli wymagana jest większa precyzja, możemy skorygować zmiany temperatury ΔrHo, wykorzystując dane dotyczące pojemności cieplnej.
To, jak ΔrHo rośnie lub maleje z temperaturą, jest związane z tym, czy entalpia reakcji jest dodatnia czy ujemna.
Wyrażenie na \(K) jest dość wrażliwą funkcją temperatury, biorąc pod uwagę jego wykładniczą zależność od różnicy współczynników stechiometrycznych Jednym ze sposobów dostrzeżenia wrażliwej zależności stałych równowagi od temperatury jest przypomnienie, że
Jednakże, ponieważ pod stałym ciśnieniem i w stałej temperaturze
równanie \(\) przyjmuje postać
Biorąc logarytm naturalny z obu stron, otrzymujemy liniową zależność pomiędzy \(\) K \) a standardowymi entalpiami i entropiami:
, która znana jest jako równanie van’t Hoffa. Wynika z niego, że wykres \(\n K\) vs. \(1/T\) powinien być linią o nachyleniu \(-Delta_r{H^o}/R\) i przechwycie \(\Delta_r{S^o}/R\).
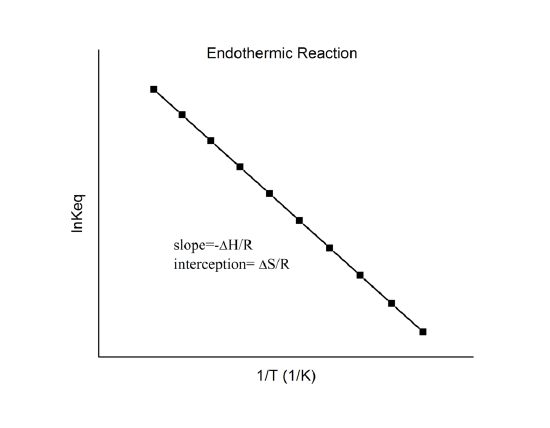
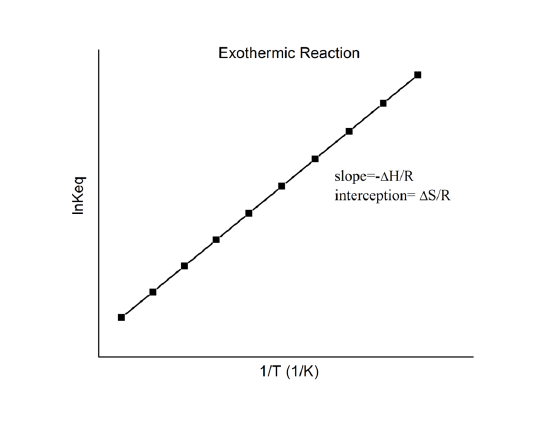
Więc, te wielkości mogą być wyznaczone z danych \(\n K\) vs. \(1/T\) bez wykonywania kalorymetrii. Oczywiście, głównym założeniem jest to, że \(\Delta_r{H^o}} i \(\Delta_r{S^o}} są tylko bardzo słabo zależne od \(T\), co zwykle jest słuszne.
Kontrybutorzy i przypisania
.