Note : ceci est la première page de notre analyse de Vortex Math. Cliquez ici si vous cherchiez l’application interactive Vortex-N-k.
Chère Professeur Puzzler,
J’ai entendu des gens parler de « Vortex Math », et je veux comprendre ce que c’est. Pouvez-vous m’aider ?
Mystifié dans le Maine
Chère Mystifiée,
Je serais heureux de vous aider. Cela va devenir un peu technique par moments, mais, pour rendre les choses intéressantes, mon bon ami Marko-11 de Wunfishia a proposé de faire un post invité. Marko-11 est un peu bizarre (littéralement) : il a onze doigts au lieu de dix, ce qui lui donne une toute nouvelle perspective des mathématiques. Si vous le suivez jusqu’au bout de son explication, je vous garantis que vous apprécierez le voyage ! Marko?
Merci, Professeur Puzzler. Je dois prévenir vos lecteurs que je vais faire un peu de théorie légère des nombres ici, mais si les maths ne sont pas leur point fort, ils peuvent laisser leurs yeux se voiler pendant les trucs de maths, et juste regarder mon commentaire sur les jolies images.
J’aimerais commencer par m’assurer que tous vos amis comprennent que tout le monde ne compte pas comme eux. La plupart de vos amis comptent probablement dans un système numérique appelé base dix, qui comporte les chiffres suivants : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Ce n’est pas inhabituel, puisqu’ils ont tous dix doigts. Moi, par contre (pour ainsi dire), je fais des calculs en base onze (vous pouvez probablement deviner pourquoi). Mon système de comptage a un chiffre supplémentaire, tout comme j’ai un chiffre supplémentaire. Mes chiffres sont 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, et A. « A ? » Vous pourriez dire, « C’est une lettre, pas un chiffre ! » C’est vrai, c’est vrai, mais chaque fois que vous travaillez dans une base supérieure à dix, vous avez besoin de chiffres supplémentaires, et plutôt que d’inventer de nouveaux symboles, nous nous contentons de récupérer les symboles qui ne sont pas utilisés pour autre chose (avec des excuses à mes amis les professeurs d’anglais !)
Maintenant, parce que je fais de l’arithmétique en base onze, j’écris les nombres très différemment. Par exemple, quand je veux écrire le nombre 34, j’écris « 31 ». Pourquoi ? Parce que cela signifie « 3 onze, plus 1 de plus ». Le nombre 87, j’écris « 7A », parce que 7 onze plus A (c’est votre nombre 10) font 87.
Je vais donc faire de l’arithmétique fantaisiste, et tout sera en base onze, donc vous devrez faire très attention pour me suivre.

Premièrement, je vais dessiner un cercle, et marquer tous mes chiffres autour de la circonférence. En fait, pas tous ; je vais sauter le zéro. Ne me demandez pas pourquoi, je ne suis pas sûr d’avoir une bonne raison, mais ça va tout arranger. Alors faites-moi confiance. J’ai onze doigts, alors comment pourrais-je me tromper ?
Ok, maintenant que j’ai dessiné mon cercle, je vais commencer à connecter les nombres, selon le schéma suivant. Je commence avec 2 et je le double. Le résultat est 4. Donc je connecte 2 et 4. Maintenant, je double 4. Le résultat est 8, donc je relie 4 et 8. Maintenant je double 8, et ça fait… uh oh… ça fait 15. (Je sais ce que vous pensez – c’est 16. Mais c’est en base dix. En base onze, 16 s’écrit 15, parce que 1 onze plus 5 autres font 16).
Bien, mais je n’ai pas de chiffre 15. Ce n’est pas grave… Je vais simplement ajouter le 1 et le 5 pour faire 6, puis je vais relier le 8 et le 6. Maintenant je double 15 (base onze) et j’obtiens 2A (c’est 32 pour vous !). Maintenant, j’ajoute les chiffres 2 + A = 11 (base onze). Comme je n’ai pas de chiffre 11, je vais additionner les chiffres : 1 + 1 = 2, et donc je vais tracer une ligne reliant 6 et 2.

Wow ! Ca a l’air vraiment cool ! C’est comme un magnifique symbole de l’infini, qui est la façon de l’univers de me dire que je suis sur quelque chose de très spécial qui résultera en un tout infini pour tout le monde !
Pour rendre cela encore plus intéressant, si je double 2A, et que je fais mon processus de mappage, il se mappe à 4, et le doublement suivant se mappe à 8, puis 6, et il se répète encore et encore et encore, ce qui, bien sûr, est un symbole de la richesse sans fin qui m’attend une fois que j’aurai vendu cette idée à d’autres Wunfishians !
Mais qu’en est-il des pauvres petits 3, 5, 7, 9, et A ? A quoi correspondent-ils ? C’est là que ça devient VRAIMENT cool ; 1 se connecte à 2, 3 à 6, 5 à A, 7 à 4, et 9 à 8. En d’autres termes, à l’exception du 5, ils alimentent tous directement le cycle de l’infini, me donnant encore plus d’énergie, de richesse et de potentiel de lutte contre le cancer que j’ai déjà découvert. Quoi ? Je ne t’ai pas parlé de la lutte contre le cancer ? Oh oui. C’est un fait.
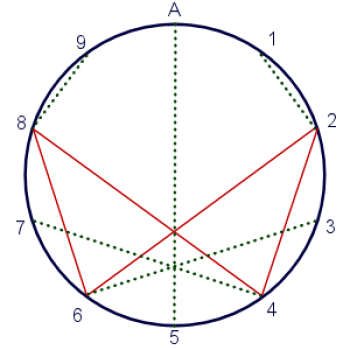
Et à quoi correspond A ? C’est la chose la plus étonnante, A se connecte à lui-même. Peu importe le nombre de fois où vous le doublez, A continue à se représenter lui-même. Cela me dit que A (votre nombre 10) est la constante magique qui régit l’univers et relie le langage divin des mathématiques.
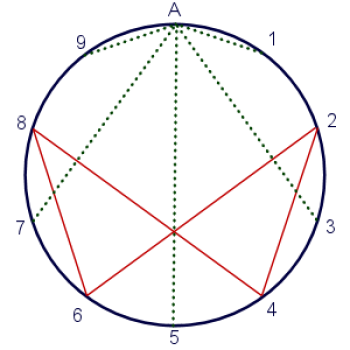
En fait, vous savez, toute cette histoire aurait l’air bien plus cool si, au lieu de mapper 1, 3, 7 et 9 dans la boucle infinie, je les mappais à mon nombre magique. Ne me demandez pas pourquoi, je n’ai pas besoin de raison. C’est juste que ça a l’air cool, alors je vais le faire.
Maintenant mon diagramme de vortex ressemble à l’infini sous un arbre de Noël, ce qui est la façon de l’univers de me dire que c’est son cadeau pour moi.
Pas du tout. Vous voyez, je n’ai pas inventé les mathématiques des vortex. Elle a été inventée par un pauvre type (j’aime l’appeler Marko-10) qui, malheureusement, n’avait que 10 doigts. Et parce qu’il n’avait que 10 doigts, il a fait la triste erreur d’essayer de faire tout cela en base dix.
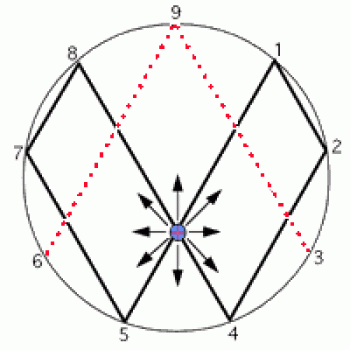
Bien sûr, son diagramme de vortex n’était pas aussi joli que le mien. Notez que son symbole de l’infini est bien moins élégant que le mien, et qu’il nécessite un doublement supplémentaire pour revenir à la bonté infinie. Notez aussi qu’il ne savait pas vraiment quoi faire avec les pauvres petits 3 et 6, qui se contentent snobement de se mettre en correspondance les uns avec les autres, et ne nourrissent pas sa réserve d’énergie infinie.
Et son arbre de Noël a-t-il seulement un tronc ? Non, il n’en a pas. Et il n’y a qu’un seul ensemble de branches, donc l’univers ne peut pas mettre beaucoup de cadeaux sous cet arbre.
C’est quoi cette espèce de flèche funky au milieu ? Apparemment ça fait de l’ensemble le symbole de l’illumination. Eh bien, aussi éclairé que vous pouvez l’être si vous êtes une créature à dix doigts ! Si vous êtes suffisamment éclairé, ce symbole vous aidera à découvrir le nom secret de Dieu – du moins, c’est ce que dit Marko-10. Mais je soupçonne que cela dépend de la question de savoir si Dieu n’a que dix doigts ou non. (Au cas où vous ne l’auriez pas encore compris, Marko-10 ne fait pas de mathématiques, il fait du mysticisme bahá’í.)
Oh, oui, et puisque Marko a dix doigts, il pense que NEUF est le nombre magique qui relie le bla-bla-bla unificateur de l’univers, et qui guérira le cancer, nous fournira de l’énergie gratuite, et guérira peut-être aussi la calvitie. Pourquoi ? Parce que, apparemment, l’univers se soucie qu’il n’ait que dix doigts au lieu de onze.
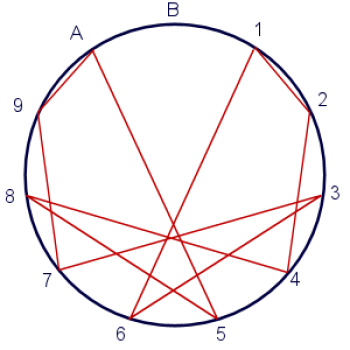
Merci pour cette explication, Marko-11. J’espère que tu feras un merveilleux voyage de retour à Wunfishia (je sais, c’est un long voyage d’ici à là, et il y a des choses drôles partout !). Oh, et merci de m’avoir présenté ton cousin de Blufishia, Marko-12 (je suis sûr que tout le monde peut comprendre pourquoi il s’appelle Marko-12). Marko-12 a fait sa propre analyse magique des nombres en base douze. Il est arrivé avec un diagramme de vortex vraiment cool qui est comme une combinaison d’un aigle et d’un pentagramme.
Coïncidence ? Je suis sûr que non. Je suis sûr que c’est la façon dont l’univers lui dit qu’il va s’élever à de grandes hauteurs s’il veut juste atteindre les étoiles.
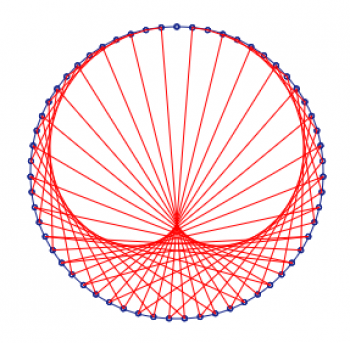
Bien sûr, même Marko-12 n’arrive pas à la cheville de l’intelligence des anciens Babyloniens ; si seulement les « mathématiciens » d’aujourd’hui basés sur les vortex étaient aussi avancés que ces gars-là, leur diagramme de vortex aurait ressemblé à cette étonnante œuvre d’art ! Et oui, il s’agit bien d’une seule boucle qui touche tous les chiffres du cercle, à l’exception du chiffre 59 de la base soixante. Avec tout le respect que je dois à Marko-10, CINQUANTE-NEUF est bien plus cool que NEUF !
Une dernière remarque : les gens du VBM (Vortex Based Math) croient que leur diagramme magique est un » code divin « , mais que vous croyiez ou non à la déclaration de Galilée » Les mathématiques sont le langage avec lequel Dieu a écrit l’univers « , on ne peut nier que la base dix est une construction entièrement humaine. Donc, si leur diagramme est « divin », alors il en est de même pour tous les innombrables (littéralement infinis !) beaux diagrammes (et les magnifiques modèles associés !) qu’ils ignorent parce qu’ils sont liés et embourbés par le nombre dix.
Il m’a fallu un grand total de 5 minutes pour développer une preuve mathématique rigoureuse que si vous travaillez en base N, N-1 a leur comportement de « nombre magique ». S’ils étaient de vrais mathématiciens, c’est le genre de travail qu’ils pourraient faire, mais ce sont des mystiques bahá’ís au lieu de mathématiciens, et ils ne peuvent pas voir la forêt à cause de leur propre petit arbre de Noël triste…
Plutôt que de perdre votre temps avec eux, amusez-vous vraiment – apprenez à travailler dans des bases autres que la base dix, puis créez vos propres diagrammes de vortex. Vous aideront-ils à créer de l’énergie libre ? Ou à guérir l’acné ? Évidemment non, mais ils sont certainement jolis, et ils fonctionnent également comme de très jolis tests de Rorchach qui vous en diront plus sur vous-même que sur la nature de l’univers.
Professeur Puzzler
P.S. Voici une aide visuelle pour vous aider à avoir un aperçu des « diagrammes de vortex » dans d’autres bases : Au-delà des mathématiques basées sur les vortex
.