La symétrie ponctuelle existe lorsque la figure est dessinée autour d’un seul point.

Ce point est appelé le centre de la figure ou le centre de la symétrie. Dans la figure ci-contre, on observe qu’en correspondance avec le point X de la figure, il existe un point X’ de l’autre côté du centre qui est directementopposé à X et se trouve sur la figure. Nous disons que la figure est symétrique par rapport au centre.
Note:
Lorsque nous faisons pivoter une figure d’environ 180° et qu’elle retrouve sa forme initiale, alors nous disons que la symétrie ponctuelle existe dans la figure.
Exemples de figures présentant une symétrie ponctuelle :
● Toutes les lettres de l’alphabet anglais.
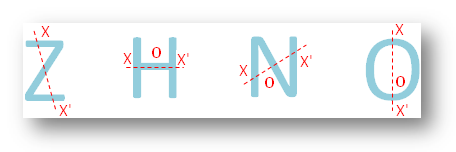
● Différentes figures géométriques.
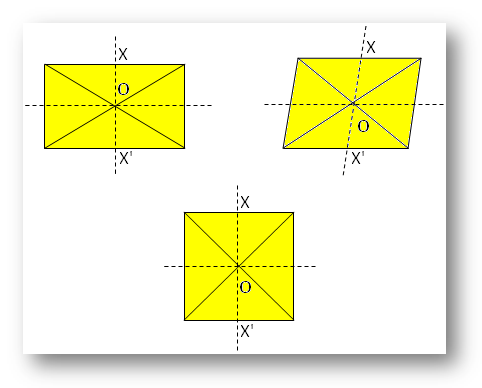
Note:
Ici, O est le centre de symétrie.
Par rapport à X, il existe X’, tel que X’ est directement opposé à X de l’autre côté de O.
Quelles sont les conditions qu’une forme ou une figure satisfait pour la symétrie ponctuelle ?
Les conditions qu’une forme ou une figure satisfait pour la symétrie ponctuelle c’est-à-dire que chaque partie doit avoir une partie correspondante
– la distance doit être égale à partir du point central
– mais doit être dans la direction opposée.
● Concepts connexes
● Symétrie linéaire
● Lignes de symétrie
● Symétrie de rotation
● Ordre de symétrie de rotation
● Types de symétrie
● Réflexion
● Réflexion d’un point dans l’axe des x-.axe
● Réflexion d’un point dans l’axe y-.axe
● Réflexion d’un point dans l’origine
● Rotation
● Rotation de 90 degrés dans le sens des aiguilles d’une montre
● Rotation de 90 degrés dans le sens inverse des aiguilles d’une montre
● Rotation de 180 degrés
.
Problèmes de mathématiques de 7e année
Pratique des mathématiques de 8e année
De la symétrie des points à la PAGE D’ACCUEIL
.