Qu’est-ce que la perméabilité de la membrane cellulaire ?
Mode lecteur
L’une des caractéristiques de signature de tous les organismes vivants est qu’ils contiennent un mélange distinctif d’ions et de petites molécules. Cette composition diffère non seulement de l’environnement mais peut également varier au sein de la cellule. Par exemple, la concentration d’ions hydrogène dans certains compartiments cellulaires peut être 104 fois plus élevée que dans d’autres (la mitochondrie atteignant un pH aussi élevé que 8 ; les lysosomes ayant un pH aussi bas que 4, BNID 107521, 106074). Le rapport des concentrations d’ions Ca2+ dans les compartiments du fluide extra- et intracellulaire peut à nouveau être multiplié par 104 (BNID 104083). Cette différence de concentration est si importante que le transport d’un ion Ca2+ à travers la membrane, du compartiment intra- vers le compartiment extracellulaire, nécessite l’énergie de plus d’un proton ou d’un ion sodium s’écoulant le long du gradient de force motrice des protons. Pour s’en convaincre, le lecteur doit se rappeler la règle empirique de notre liste de trucs et astuces, selon laquelle l’établissement d’une différence de potentiel d’un ordre de grandeur nécessite 6 kJ/mol (≈2 kBT). Cette énergie peut être atteinte par exemple par le transport d’une charge électrique à travers une différence de potentiel de 60 mV. Pour atteindre un rapport de concentration de quatre ordres de grandeur, il faudrait alors qu’une charge parcoure environ 240 mV de force motrice électronique (en réalité encore plus en raison de la double charge de l’ion calcium). Ceci est très proche de la tension de claquage de la membrane, comme discuté dans la vignette « Quelle est la différence de potentiel électrique à travers les membranes ? ». En effet, le rapport de concentration élevé de Ca2+ est généralement obtenu en se couplant au transport de trois ions sodium ou à l’hydrolyse de l’ATP, ce qui permet d’obtenir la différence de densité requise sans énergiser dangereusement la membrane.
La deuxième loi de la thermodynamique nous enseigne qu’en général, la présence de gradients de concentration sera finalement saignée par les processus de transport de masse, qui conduisent régulièrement les systèmes vers un état d’équilibre. Cependant, bien que la deuxième loi de la thermodynamique nous indique la nature de l’état ultime d’un système (par exemple, des concentrations uniformes), elle ne nous dit pas combien de temps il faudra pour atteindre cet état. Les membranes ont évolué pour former une barrière très efficace au transfert spontané de nombreuses espèces ioniques et moléculaires. Pour estimer l’échelle de temps nécessaire à l’égalisation des concentrations, nous devons connaître les taux de transport de masse, qui dépendent de propriétés matérielles clés telles que les constantes de diffusion et les perméabilités.
Une classe de « lois » extrêmement réussie, qui décrit le comportement de systèmes ayant subi un petit écart par rapport à l’équilibre, sont les lois de transport linéaire. Ces lois posent une relation linéaire simple entre le taux de transport d’une certaine quantité d’intérêt et la force motrice associée. Pour le transport de masse, il existe une relation linéaire entre le flux (c’est-à-dire le nombre de molécules traversant une unité de surface par unité de temps) et la différence de concentration (qui sert de force motrice). Pour le transport à travers les membranes, ces idées ont été codifiées dans l’équation simple (pour un soluté neutre) j= – p-(cin-cout), où j est le flux net dans la cellule, cin et cout se réfèrent aux concentrations à l’intérieur et à l’extérieur de la région liée à la membrane, et p est un paramètre matériel connu sous le nom de perméabilité. Les unités de p peuvent être déduites en notant que le flux a pour unité le nombre/(surface x temps) et que la concentration a pour unité le nombre/volume, ce qui implique que les unités de p lui-même sont la longueur/le temps. Comme de nombreuses quantités de transport (par exemple, les conductivités électriques des matériaux qui s’étendent sur plus de 30 ordres de grandeur), la perméabilité a une très grande plage dynamique, comme l’illustre la figure 1. Comme on peut le voir sur la figure, les bicouches lipidiques ont une gamme de perméabilités de près de 1010 fois.
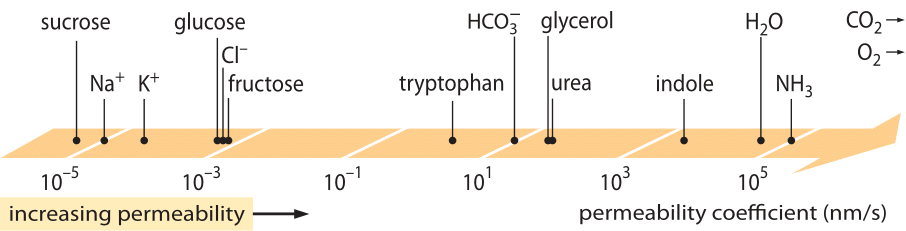
Figure 1 : La large gamme de perméabilités membranaires de différents composés dans la cellule. Les membranes sont plus perméables aux composés non chargés et moins perméables aux ions chargés. Notez que l’existence de canaux ioniques rend la perméabilité apparente lorsqu’ils sont ouverts plusieurs ordres de grandeur plus élevés. Les unités sont choisies comme nm/s et plusieurs nm sont la largeur caractéristique de la membrane. Figure adaptée de R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. La valeur pour le glucose est plus petite que dans Robertson, d’après plusieurs sources telles que BNID 110830, 110807. Autres sources de données : BNID 110729, 110731, 110816, 110824, 110806.
Quels paramètres physico-chimiques guident la localisation d’un composé sur cette échelle de perméabilités ? Une règle empirique est que les petites molécules ont des perméabilités plus élevées que les grosses molécules. Une autre règle empirique est que les composés neutres peuvent traverser la membrane plusieurs ordres de grandeur plus rapidement que les composés chargés similaires. Parmi les composés chargés, les composés négatifs (anioniques) ont tendance à avoir des perméabilités beaucoup plus élevées que les composés positifs (cationiques). La règle dite d’Overton stipule que la perméabilité de la membrane augmente avec l’hydrophobie, l’hydrophobie étant la tendance d’un composé à préférer un solvant non polaire à un solvant polaire (aqueux). La règle d’Overton prédit que les molécules chargées (non hydrophobes), telles que les ions, auront tendance à avoir une faible perméabilité car elles subissent une pénalité énergétique associée à la pénétration de la membrane, tandis que les gaz dissous tels que l’O2 et le CO2, qui sont hydrophobes (car non chargés et symétriques), auront une perméabilité élevée. En effet, la perméabilité des membranes bicouches lipidiques au CO2 donne des valeurs de 0,01-1 cm/s (oui, les mesures de perméabilité ont des incertitudes très élevées entre les différents laboratoires, BNID 110004, 110617, 102624), supérieures à toutes les autres valeurs présentées dans la figure 1. Cette valeur montre que la barrière créée par la membrane cellulaire est en fait un obstacle moins important que la barrière causée par la couche d’eau non remuée qui engloutit la membrane cellulaire de l’extérieur. Une telle déduction peut être dérivée de l’équation du coefficient de perméabilité d’un obstacle, donnée par p=K x D/l où l est la largeur, D le coefficient de diffusion et K le coefficient de partage entre le milieu et le matériau de l’obstacle. Cette formule est également connue sous le nom de modèle de perméabilité « solubilité-diffusion », où l’on désigne les effets K et D qui sont deux étapes affectant la perméabilité. Pour une couche d’eau non agitée, K=1 car elle est très similaire au milieu, mais pour une membrane, la valeur pour tous les matériaux, sauf les plus hydrophobes, est généralement inférieure de plusieurs ordres de grandeur à 1. Cette dépendance de K est au cœur de la règle d’Overton mentionnée ci-dessus. La perméabilité élevée pour le CO2 suggère également que les canaux tels que les aquaporines qui ont été suggérés pour servir au transport du gaz dans la cellule ne sont pas nécessaires car la membrane est suffisamment perméable. Pour voir comment les propriétés de la membrane affectent la composition chimique des métabolites, nous nous tournons vers le calcul du temps de fuite pour différents composés
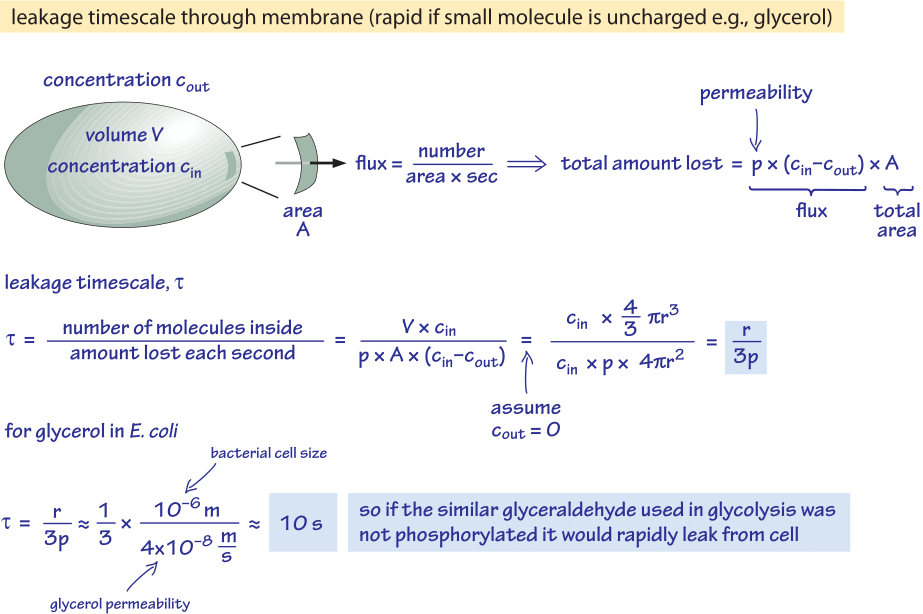
Figure 2 : Calcul du temps de diffusion passive d’une molécule de glucose non phosphorylée hors d’une cellule bactérienne. Les implications fonctionnelles sont ensuite considérées pour une cellule à croissance rapide où l’effet est négligeable et pour les cellules en état stationnaire où il peut provoquer une fuite appréciable de ressources.
Nous considérons le glycérol, par exemple. L’analyse présentée dans la figure 2 donne une estimation du temps de sa fuite hors de la cellule si la molécule n’est pas phosphorylée ou autrement convertie en une forme plus hydrophile. La perméabilité de la membrane cellulaire au glycérol est p≈10-100 nm/s (BNID 110824) comme on peut le lire sur la figure 1. L’échelle de temps pour qu’une molécule de glycérol à l’intérieur de la cellule s’échappe à nouveau vers le milieu environnant, en supposant qu’il n’y a pas de retour dans la cellule (cout=0), peut être grossièrement estimée en notant que l’efflux de la cellule est p-A-cin où A est la surface de la cellule. L’échelle de temps est trouvée en prenant la quantité totale dans la cellule, V-cin (où V est le volume de la cellule ou plus exactement le volume d’eau de la cellule), et en divisant par ce flux résultant pour une cellule bactérienne (r≈1 μm) en une échelle de temps :
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
C’est une estimation grossière car nous n’avons pas tenu compte de la diminution de la concentration de cin avec le temps qui donnera un facteur de correction de 1/ln(2), c’est-à-dire moins de 2 fois plus. Ce que nous apprenons de ces estimations, c’est que si les intermédiaires glycolytiques que sont le glycéraldéhyde ou le dihydroxyacétone, qui sont très similaires au glycérol, n’étaient pas phosphorylés, ce qui entraîne l’ajout d’une charge, ils seraient perdus dans le milieu par diffusion à travers la membrane cellulaire. Dans les milieux de laboratoire, où une source de carbone est fournie en abondance, ce n’est pas un problème majeur, mais dans un environnement naturel où les cellules attendent souvent en phase stationnaire une impulsion chanceuse de nutriments (E. coli est censé passer des mois sans croissance après son excrétion du corps avant de trouver un nouvel hôte), la cellule peut freiner ses pertes en s’assurant que les intermédiaires métaboliques sont marqués d’une charge qui les empêchera de retraverser la barrière présentée par la bicouche lipidique.





.