Si vous aimez boire, alors une bouteille de Klein n’est pas un réceptacle recommandé. Elle peut ressembler vaguement à une bouteille, mais elle n’enferme aucun volume, ce qui signifie qu’elle ne peut réellement contenir aucun liquide. Tout ce que vous versez « dedans » ressortira simplement.
Comment construire une chose aussi étrange et pourquoi vouloir la construire ? Le mathématicien Felix Klein, qui a découvert la bouteille en 1882, l’a décrite comme une surface qui « peut être visualisée en inversant un morceau d’un tube en caoutchouc et en le laissant passer à travers lui-même de sorte que l’extérieur et l’intérieur se rencontrent ».
Votre navigateur ne prend pas en charge la balise vidéo.Lien direct
Il est évident que la bouteille de Klein, tout comme la sphère plus familière, est une surface fermée : elle est finie dans le sens où l’on peut la faire rentrer dans une région finie de l’espace, mais une fourmi pourrait s’y promener éternellement sans jamais rencontrer de limite ou tomber par-dessus un bord. Contrairement à la sphère, qui a un intérieur et un extérieur, la bouteille de Klein est unilatérale : en se promenant, notre fourmi pourrait atteindre les deux côtés de chaque point de la surface. C’est pourquoi la bouteille n’enferme aucun volume, et cela répond également à la question « pourquoi » : la bouteille de Klein est intéressante parce que nous ne rencontrons pas beaucoup de formes unilatérales dans la nature. (Voir ici une autre très jolie image d’une bouteille de Klein.)

Le ruban de Möbius est unilatéral – regardez la version animée. (Image et animation de Konrad Polthier.)
Si cela est un peu confus, pensez à un exemple plus simple de surface unilatérale : le fameux ruban de Möbius. Vous pouvez en fabriquer un en prenant les deux extrémités d’une bande de papier, en donnant une torsion à la bande, puis en collant les extrémités ensemble. En utilisant une bande de papier dont les deux côtés sont de couleurs différentes, par exemple vert et orange, il est facile de se convaincre que le ruban de Möbius obtenu est unilatéral. Une fois que vous aurez tordu et collé, vous constaterez que vous pouvez atteindre chaque point orange à partir de chaque point vert sans avoir à percer le papier ou à grimper sur son bord.
Contrairement à la bouteille de Klein, le ruban de Möbius a bien une frontière – elle est constituée des deux bords non collés de la bande initiale. Mais il existe un lien entre les deux. Si vous prenez deux bandes de Möbius et créez une forme fermée en joignant leurs limites à l’aide d’une bande ordinaire à deux côtés, comme indiqué ci-dessous, ce que vous obtenez est exactement la bouteille de Klein.
Votre navigateur ne prend pas en charge la balise vidéo.Lien direct
dont les faces arrière et avant sont respectivement colorées en blanc et en bleu. Animation par Konrad Polthier.
Ce fait a inspiré au mathématicien Leo Moser un limerick:
Un mathématicien nommé KleinPensait que la bande de Möbius était divine.Il a dit : « Si vous collez les bords de deux, vous obtiendrez une bouteille bizarre comme la mienne. »
Certains mathématiciens sont vraiment multi-talents !
Une autre caractéristique curieuse de la bouteille de Klein est qu’elle se recoupe elle-même, ce qui signifie qu’il est difficile de la fabriquer à partir d’un seul tube de caoutchouc comme Klein l’a suggéré. À proprement parler, l’objet qui s’auto-intersecte représenté ci-dessus n’est pas une bouteille de Klein, mais (comme Klein l’a indiqué) seulement une visualisation de celle-ci. Pour comprendre pourquoi, il faut d’abord penser au beignet plus familier (connu mathématiquement comme un tore). Vous pouvez fabriquer un tore à partir d’une feuille carrée de caoutchouc en collant d’abord deux côtés opposés pour former un cylindre, puis en collant les deux composantes limites de ce cylindre pour obtenir le tore.

Faire un tore : Commencez par coller des points opposés sur deux côtés opposés du carré pour faire un cylindre, puis collez les deux cercles de délimitation de ce cylindre (correspondant au collage de points opposés sur les deux autres côtés du carré) pour former un tore.
Si vous ne voulez pas vous embêter avec le collage, vous pouvez simplement considérer le tore comme un carré, en gardant à l’esprit que les points opposés sur les côtés opposés sont considérés comme identiques. Ainsi, lorsque vous faites glisser une forme dessinée sur le « carré » sur le bord supérieur, elle réapparaîtra sur le bord inférieur et lorsque vous la faites glisser sur le bord droit, elle réapparaîtra sur le bord gauche (et vice versa).
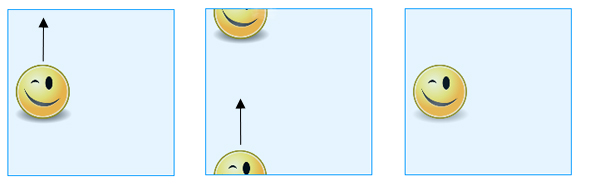
Lorsque vous faites glisser une forme dessinée sur le « carré » à travers le bord supérieur, elle réapparaîtra au bord inférieur.
Pour obtenir une vraie bouteille de Klein, commencez de la même manière, en identifiant les points opposés sur une paire de côtés opposés d’un carré. Pour l’autre paire de côtés, cependant, n’identifiez pas des points directement opposés, mais des points diagonalement opposés, comme le montre l’image.
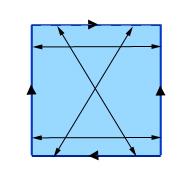
Faire une bouteille de Klein : identifiez les points opposés de deux côtés opposés (les verticaux sur cette image), puis identifiez les points diagonalement opposés sur les deux autres côtés. (Si vous étiquetez les points des côtés supérieur et inférieur de gauche à droite par les chiffres 0 à 1, alors un point avec l’étiquette x sur le côté supérieur est identifié avec le point avec l’étiquette 1-x sur le côté inférieur.)
L’objet résultant est la bouteille de Klein. Encore une fois, vous pouvez la considérer comme un carré, en gardant à l’esprit quels points de la frontière sont considérés comme identiques. Si vous faites glisser une forme sur l’un des bords dont les points opposés ont été identifiés (vertical dans notre image), elle réapparaît sur le côté opposé, comme avant. Si, par contre, vous la faites glisser sur l’une des arêtes dont les points ont été identifiés en diagonale (horizontale dans notre image), elle apparaît sur le côté opposé, mais déplacée et comme une image miroir de son moi original.
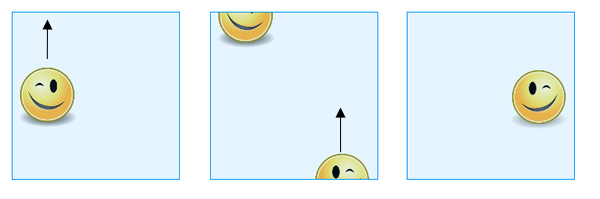
Si vous faites glisser une forme sur l’arête supérieure, elle apparaît sur l’arête inférieure, mais décalée et comme une image miroir de son soi original.
La seule façon de construire cette forme dans l’espace tridimensionnel en collant réellement des points ensemble est de lui permettre de s’intersecter elle-même. Cela revient à identifier des paires de points à l’intérieur du carré d’origine, donc à proprement parler la forme résultante n’est pas exactement la même que la bouteille de Klein, qui n’a que des points limites identifiés. C’est juste une façon de représenter la bouteille dans un espace tridimensionnel (il y en a d’autres aussi).
Votre navigateur ne supporte pas la balise vidéo.Lien direct
Image miroir et orientabilité. Animation de Konrad Polthier.
Curieusement, les concepts d' »intérieur », d' »extérieur » et de « unilatéralité » dépendent de l’espace ambiant dans lequel un objet est assis. Par exemple, une boucle dessinée sur une feuille de papier (dans un espace bidimensionnel) a un intérieur et un extérieur bien définis, mais une boucle dessinée dans un espace tridimensionnel n’en a pas. C’est pourquoi nous ne pouvons pas parler d’unilatéralité si nous ne décidons pas d’abord comment intégrer une surface dans un espace tridimensionnel. Il existe cependant une propriété étroitement liée qui est intrinsèque à une forme et ne dépend pas de l’espace environnant. Une surface est dite orientable si vous ne pouvez pas faire glisser une forme dessinée sur elle et la ramener à son point de départ de manière à ce qu’elle ressemble à sa propre image miroir. Comme vous pouvez le voir dans l’animation accompagnant l’image de droite, le ruban de Möbius n’est pas orientable. Et comme vous pouvez le voir sur l’image avec le visage souriant ci-dessus, la bouteille de Klein non plus.Pour lui donner sa description mathématique complète, la bouteille de Klein est une surface fermée et non orientable. Pour en savoir plus à son sujet, voir l’article A l’intérieur de la bouteille de Klein.
A propos de l’auteur
Marianne Freiberger est rédactrice en chef de Plus.