Avant de commencer, nous devons faire quelques hypothèses.
Premièrement, nous travaillons avec des fluides newtoniens. C’est la façon mathématique la plus simple de rendre compte de la viscosité dans un fluide. Il n’y a pas de fluides réels qui entrent parfaitement dans cette catégorie, mais dans la plupart des cas, l’air et l’eau peuvent être traités comme un fluide newtonien. L’autre hypothèse très importante que nous faisons est que le fluide est incompressible. Cela signifie que sa densité, rho, est une constante.
Conservation de la masse

La première équation nous indique que la masse du fluide sur lequel nous travaillons est conservée. Le fluide peut changer de forme mais cette équation nous dit que la masse est la même du début à la fin.
Maintenant, parlons mathématiques. La lettre u représente la vitesse du fluide et c’est un vecteur. Elle a trois composantes, nous pouvons les appeler u, v, w et elles représentent la vitesse du fluide dans la direction x, y et z. La lettre grecque nabla ∇ suivie d’un point est l’opérateur de divergence. Cela signifie que nous devons différencier ses composantes dans chaque direction (dans ce cas x, y, z).

La première dérivée nous indique comment la composante x de la vitesse change lorsque nous nous déplaçons sur la direction x. Il en va de même pour les deux autres dérivées. Comme cette équation est égale à zéro, elle nous montre que la masse est conservée.
Conservation de la quantité de mouvement

La deuxième équation est en fait un ensemble de trois équations différentielles. C’est celle qui peut être décrite comme la deuxième loi de Newton pour les fluides. Si on développe l’expression, on obtient un système complexe.
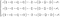
Puisqu’elle est beaucoup plus simple à comprendre, nous allons nous concentrer sur la conservation de la quantité de mouvement non développée.
Lorsque nous travaillons avec des fluides, nous pouvons dire que la masse et la densité sont les mêmes choses (tant que leur volume est le même). Si nous considérons deux fluides, nous pouvons dire que le plus dense est le plus « lourd » (par exemple, le mercure et l’eau). Dans ce cas, la lettre grecque ρ (rho) est la densité du fluide.
Nous avons la masse, maintenant pour revenir à la deuxième loi de Newton nous avons besoin de l’accélération. C’est exactement le résultat de la dérivée temporelle du vecteur vitesse.

Maintenant, il ne nous reste que les termes à droite du signe égal, et ceux-ci représentent toutes les forces qui sont appliquées au fluide.
Le premier terme ∇p est le gradient de la pression. Il représente la différence de pression dans l’espace où est contenu le fluide. Par exemple, s’il y a une zone avec une faible pression et une autre avec une pression plus élevée, le fluide se déplacera de la section à haute pression vers celle à basse pression. Le gradient de p dit tout cela.
Le deuxième terme décrit la viscosité du fluide. Pensez à deux liquides différents, comme l’eau et le miel. Lorsque vous versez un verre d’eau, il tombe rapidement et facilement. Quand vous faites la même chose avec du miel, il est collant et se verse très lentement. C’est ce que dit cette expression.
Le dernier terme, F, est le plus facile car il représente toutes les forces externes qui peuvent être appliquées à ce fluide. Habituellement, la force que nous considérons ici est la gravité.
C’est tout, tous ces symboles fantaisistes et la lettre signifient est juste force = masse x accélération.
Utilisation des équations de Navier-Stokes
Puisque la résolution de ces équations est si compliquée, pour les utiliser nous devons faire beaucoup d’approximations. Quelques exemples sont les écoulements de Poiseuille et de Couette. Avec beaucoup d’hypothèses, ces deux scientifiques ont pu trouver une solution aux équations de Navier-Stokes pour une application très spécifique. Cependant, si nous voulons les utiliser pour une tâche plus compliquée, comme les prévisions météorologiques, nous devons faire autre chose.
La façon la plus courante d’utiliser ces équations est de les transformer, avec la moyenne de Reynolds. C’est un processus mathématique avancé et les résultats sont les équations de Reynolds. Elles sont généralement appelées équations RANS (qui signifie Reynolds averaged Navier-Stokes).
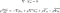
Ces équations sont utilisées lorsque le fluide est dans un écoulement turbulent. Elles ressemblent presque exactement aux équations de Navier-Stokes, sauf pour le dernier terme. Celui-ci est appelé tenseur des contraintes de Reynolds. C’est la quantité qui permet de rendre compte de la turbulence dans le fluide.
Dans les équations RANS, les quantités que nous utilisons sont moyennées sur un intervalle de temps. Cet intervalle doit être suffisamment petit pour permettre l’observation du phénomène que nous étudions. En même temps, il doit être assez grand pour que l’effet de la turbulence perde de son importance.
Avec les bonnes hypothèses, ces équations fonctionnent. Nous savons comment les utiliser pour rendre les voitures de F1 plus rapides, pour qu’un vaisseau spatial se rende à l’ISS, et pour faire les prévisions météorologiques. Alors vous vous demandez peut-être pourquoi la preuve de ces équations vaut un million de dollars ?
Un prix d’un million de dollars
D’un point de vue physique, ces équations sont juste la deuxième loi de Newton qui fonctionne avec les fluides. Lorsque nous faisons quelques hypothèses et quelques simplifications, nous pouvons faire des choses étonnantes avec elles.
Le vrai problème est le suivant . Résoudre ces équations sans approximations est juste terriblement compliqué. C’est tellement difficile qu’il n’a pas été prouvé que les solutions existent réellement. Et c’est là que le prix du millénaire entre en jeu.
L’énoncé officiel du problème (à trouver ici) est :
Preuve ou donne un contre-exemple de l’affirmation suivante : en trois dimensions d’espace et de temps, étant donné un champ de vitesse initial, il existe un vecteur vitesse et un champ de pression scalaire, qui sont tous deux lisses et globalement définis, qui résolvent les équations de Navier-Stokes.
Ce que cela signifie, c’est que pour gagner le prix, vous devez faire trois choses :
- Pour prouver qu’une solution existe
- La solution doit exister en chaque point de l’espace
- La solution doit être lisse. Cela signifie qu’un petit changement dans les conditions initiales ne produit qu’une petite variation du résultat.
Pour un ingénieur est généralement suffisant de savoir que ces équations fonctionnent, même si seulement à un certain niveau d’approximation. Pourtant, pour un mathématicien est très important de savoir si les solutions existent et comment elles se comportent.
Vous pouvez maintenant penser que si elles fonctionnent comme elles le font, passer du temps et de l’énergie à chercher une preuve est une perte de temps totale. Eh bien, comme beaucoup d’avancées technologiques dans l’histoire de l’humanité, le résultat peut ne pas sembler très important. Ce qui est important, c’est le chemin pour y arriver, qui peut apporter de nouvelles connaissances et des améliorations à notre vie.
Pensez aux missions spatiales. Si les humains n’avaient jamais décidé d’aller marcher sur la lune, nous n’aurions pas beaucoup d’objets qui sont utilisés pour améliorer notre vie. Les appareils IRM et les pacemakers proviennent de technologies développées pour l’exploration spatiale. Aujourd’hui, les médecins du monde entier les utilisent tous les jours pour sauver des vies. Il en va de même ici. La découverte de la solution des équations de Navier-Stokes nous aidera à améliorer notre compréhension des fluides et plus encore. Elle peut nous conduire à de nouvelles découvertes et nécessitera probablement l’invention de nouvelles mathématiques. Celles-ci pourront ensuite être utilisées pour répondre à de nombreux autres problèmes, pour inventer de nouvelles technologies qui amélioreront notre vie et nous rendront meilleurs.