Construire un triangle équilatéral – MathBitsNotebook (Geo

Triangle équilatéral MathBitsNotebook.com Schéma thématique | Schéma de géométrie | Ressources pour enseignants de MathBits Conditions d’utilisation Personne à contacter : Donna Roberts

Utilisez uniquement votre compas et votre règle pour dessiner une construction. Pas de dessin à main levée!

Nous allons faire TROIS constructions d’un triangle équilatéral. La première consistera à construire un triangle équilatéral étant donné la longueur d’un côté, et les deux autres consisteront à construire un triangle équilatéral inscrit dans un cercle.

Étant donné : la longueur d’un côté du triangle Construire : un triangle équilatéral

Étapes:
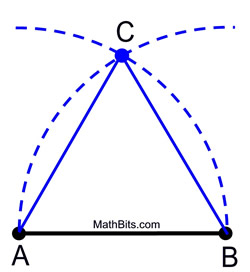
1. Placez votre point de compas sur A et mesurez la distance au point B. Balancez un arc de cette taille au-dessus (ou en dessous) du segment.
2. Sans changer la portée du compas, placez le point de compas sur B et balancez le même arc, en croisant le premier arc.
3. Indiquez le point d’intersection comme étant le troisième sommet du triangle équilatéral.

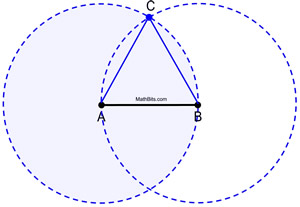
Voyez les cercles complets au travail.

Preuve de la construction : Le cercle A est congru au cercle B, puisqu’ils ont été formés chacun en utilisant la même longueur de rayon, AB. Puisque AB et AC sont des longueurs de rayons du cercle A, ils sont égaux l’un à l’autre. De même, AB et BC sont des rayons du cercle B, et sont égaux l’un à l’autre. Par conséquent, AB = AC = BC par substitution (ou propriété transitive). Puisque les segments congrus ont des longueurs égales, et ΔABC est équilatéral (ayant trois côtés congrus).

ÉTAPES:
1. Placez le point de votre compas sur le papier et tracez un cercle. (Gardez cette portée de compas !)
2. Placez un point, marqué A, n’importe où sur la circonférence du cercle pour servir de point de départ.
3. Sans changer l’envergure du compas, placez la pointe du compas sur A et balancez un petit arc traversant la circonférence du cercle.
4. Sans changer l’envergure du compas, déplacez la pointe du compas à l’intersection de l’arc précédent et de la circonférence et faites un autre petit arc sur la circonférence du cercle.
5. Continuez à répéter ce processus de « pas » autour du cercle jusqu’à ce que vous reveniez au point A.
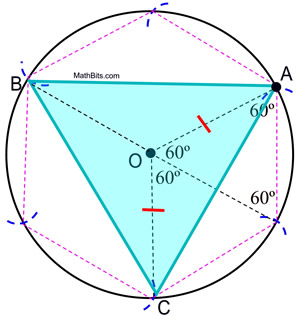
6. En partant de A, reliez tous les autres arcs du cercle pour former le triangle équilatéral.

Référez-vous à la preuve d’un hexagone régulier inscrit pour plus d’informations concernant la preuve de cette construction.

Preuve de la construction : La preuve de l’hexagone régulier inscrit montre que les angles centraux d’un hexagone régulier contiennent 60º. Les angles centraux du triangle inscrit dans ce cercle contiennent 120º. Puisque ΔAOC est isocèle (OA et OC sont des longueurs de rayons), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA par SAS. Par CPCTC, ∠OCB ∠OCA et m∠OCB = 30º par substitution et m∠BCA = 60º. De façon similaire, on a m∠ACB = m∠CBA = m∠BAC = 60º et ΔABC équilatéral.

ÉTAPES:
1. Placez le point de votre compas sur le papier et dessinez un cercle, O. (Gardez cette portée du compas !)
2. À l’aide d’une règle, tracez un diamètre du cercle, en étiquetant les points d’extrémité P et B.
3. Sans changer la portée du compas, placez le point du compas sur P et dessinez un cercle complet.
4. Étiquetez les points d’intersection des deux circonférences du cercle avec A et C.
5. Tracez des segments de A à B, B à C et C à A, pour former le triangle équilatéral.

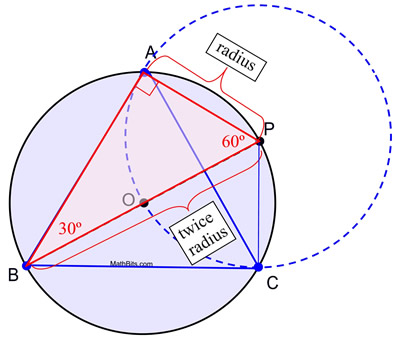
Preuve de la construction : Cette construction utilise le fait qu’un angle inscrit dans un demi-cercle est un angle droit, et que dans un triangle 30º-60º-90º, la longueur de la branche courte est la moitié de la longueur de l’hypoténuse. Dans cette construction, le cercle O et le cercle P sont congruents puisqu’ils ont la même longueur de rayon. AP est un rayon du cercle P et les rayons AP = OP. OP est également un rayon du cercle O (ainsi que OB) et le diamètre BP = BO + OP = 2 OP. Par substitution, BP = 2 AP, ce qui crée les conditions nécessaires pour que m∠ABP = 30º. Par conséquent, m∠APB = 60º. Un argument similaire peut être utilisé pour établir que pour ΔPBC, m∠PBC = 30º et m∠BPC = 60º rendant ΔPBC ΔPBA par ASA (avec le côté partagé de B à P).
Maintenant, puisque ce sont les côtés correspondants des deux triangles congrus, rendant ΔABC isocèle. ∠BAC ∠BCA puisque les angles de base d’un triangle isocèle sont congrus.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º par le postulat de l’addition des angles et la substitution. m∠BAC + m∠BCA + m∠ABC = 180º car la somme des mesures des angles dans un triangle est de 180º. Puisque m∠BAC + m∠BAC + 60º = 180º par substitution, nous savons que 2m∠BAC = 120º et m∠BAC = 60º. Par conséquent, m∠BCA est également égal à 60º par substitution, ce qui rend ΔABC équilatéral.