Comprendre les réseaux LSTM

Réseaux neuronaux récurrents

Les humains ne recommencent pas leur réflexion à zéro à chaque seconde. Lorsque vous lisez cet essai, vous comprenez chaque mot en fonction de votre compréhension des mots précédents. Vous ne jetez pas tout et recommencez à penser à partir de zéro. Vos pensées ont de la persistance.

Les réseaux neuronaux traditionnels ne peuvent pas faire cela, et cela semble être un défaut majeur. Par exemple, imaginez que vous voulez classer quel type d’événement se produit à chaque moment d’un film. On ne voit pas bien comment un réseau neuronal traditionnel pourrait utiliser son raisonnement sur les événements précédents du film pour informer les événements ultérieurs.

Les réseaux neuronaux récurrents abordent ce problème. Ce sont des réseaux comportant des boucles, permettant à l’information de persister.

Dans le schéma ci-dessus, un morceau de réseau neuronal, \(A\), regarde une certaine entrée \(x_t\) et sort une valeur \(h_t\). Une boucle permet de faire passer l’information d’une étape du réseau à la suivante.

Ces boucles font que les réseaux neuronaux récurrents semblent plutôt mystérieux. Cependant, si vous réfléchissez un peu plus, il s’avère qu’ils ne sont pas si différents d’un réseau neuronal normal. Un réseau neuronal récurrent peut être considéré comme de multiples copies du même réseau, chacune transmettant un message à son successeur. Considérez ce qui se passe si nous déroulons la boucle :

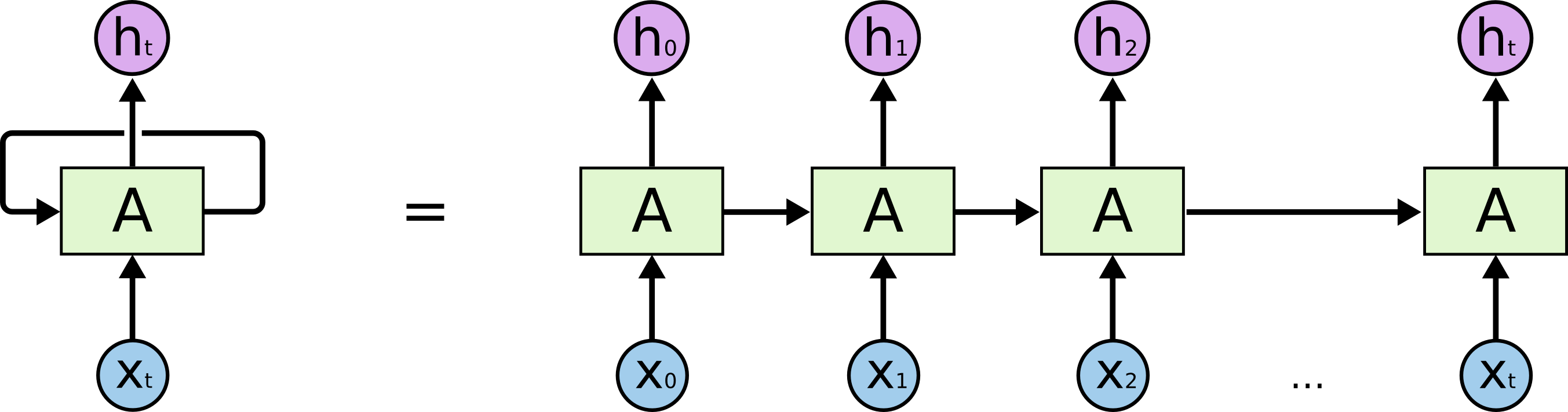
Cette nature en chaîne révèle que les réseaux neuronaux récurrents sont intimement liés aux séquences et aux listes. Ils sont l’architecture naturelle de réseau neuronal à utiliser pour de telles données.

Et ils sont certainement utilisés ! Au cours des dernières années, des succès incroyables ont été obtenus en appliquant les RNN à une variété de problèmes : reconnaissance vocale, modélisation du langage, traduction, sous-titrage d’images… La liste est longue. Je laisserai la discussion des exploits incroyables que l’on peut réaliser avec les RNN à l’excellent billet de blog d’Andrej Karpathy, The Unreasonable Effectiveness of Recurrent Neural Networks. Mais ils sont vraiment très étonnants.

L’élément essentiel de ces succès est l’utilisation des  » LSTM « , un type très spécial de réseau neuronal récurrent qui fonctionne, pour de nombreuses tâches, beaucoup mieux que la version standard. C’est avec eux que sont obtenus presque tous les résultats passionnants basés sur les réseaux neuronaux récurrents. Ce sont ces LSTM que cet essai va explorer.

Le problème des dépendances à long terme

L’un des attraits des RNN est l’idée qu’ils pourraient être en mesure de connecter des informations antérieures à la tâche actuelle, comme l’utilisation de trames vidéo précédentes pourrait informer la compréhension de la trame actuelle. Si les RNNs pouvaient faire cela, ils seraient extrêmement utiles. Mais le peuvent-ils ? Cela dépend.

Parfois, nous avons seulement besoin de regarder les informations récentes pour effectuer la tâche actuelle. Par exemple, considérons un modèle de langage qui essaie de prédire le prochain mot en fonction des précédents. Si nous essayons de prédire le dernier mot dans  » les nuages sont dans le ciel « , nous n’avons pas besoin d’un contexte supplémentaire – il est assez évident que le prochain mot sera ciel. Dans de tels cas, où l’écart entre les informations pertinentes et l’endroit où elles sont nécessaires est faible, les RNN peuvent apprendre à utiliser les informations passées.

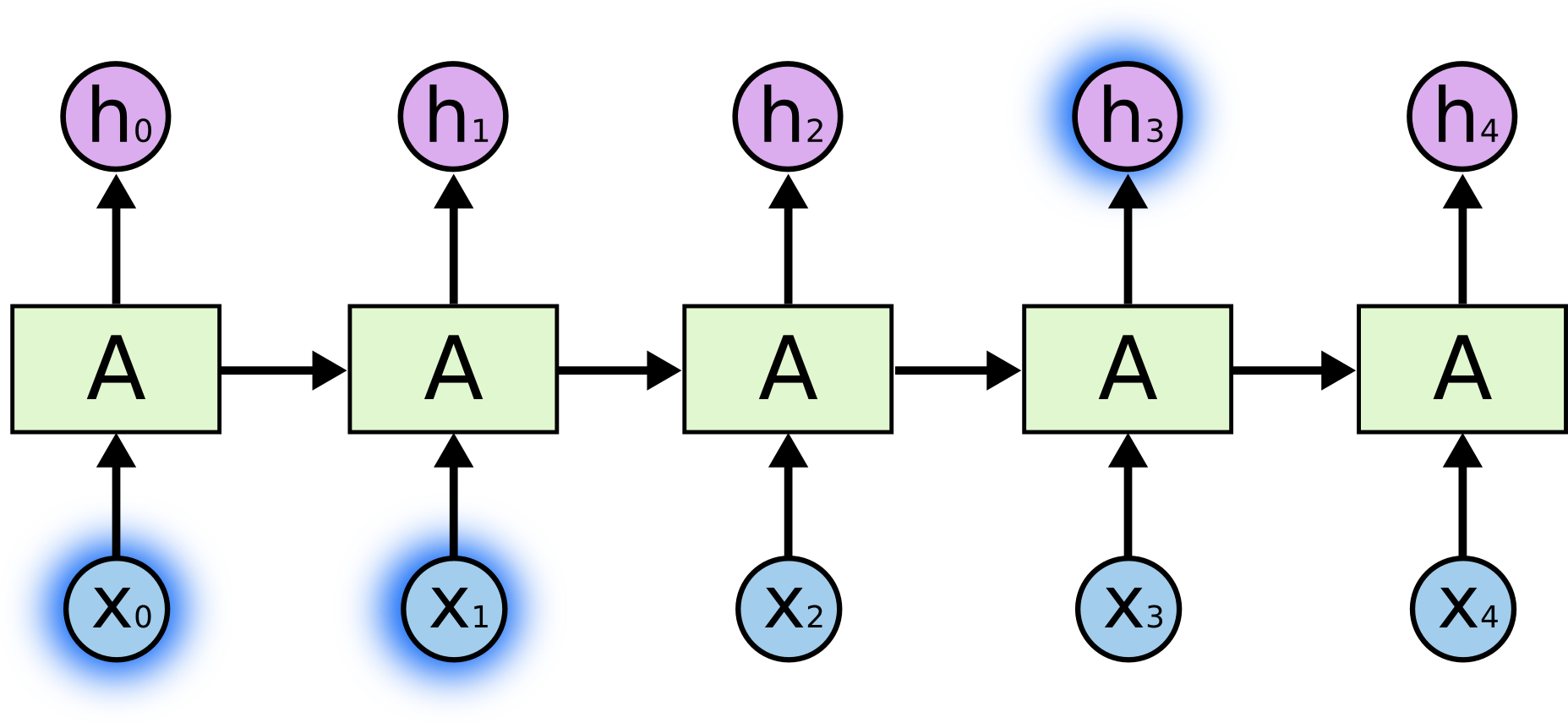
Mais il y a aussi des cas où nous avons besoin de plus de contexte. Considérons le fait d’essayer de prédire le dernier mot du texte « J’ai grandi en France… Je parle couramment le français. » Des informations récentes suggèrent que le prochain mot est probablement le nom d’une langue, mais si nous voulons affiner quelle langue, nous avons besoin du contexte de la France, plus ancien. Il est tout à fait possible que l’écart entre les informations pertinentes et le point où elles sont nécessaires devienne très important.

Malheureusement, à mesure que cet écart s’accroît, les RNN deviennent incapables d’apprendre à connecter les informations.

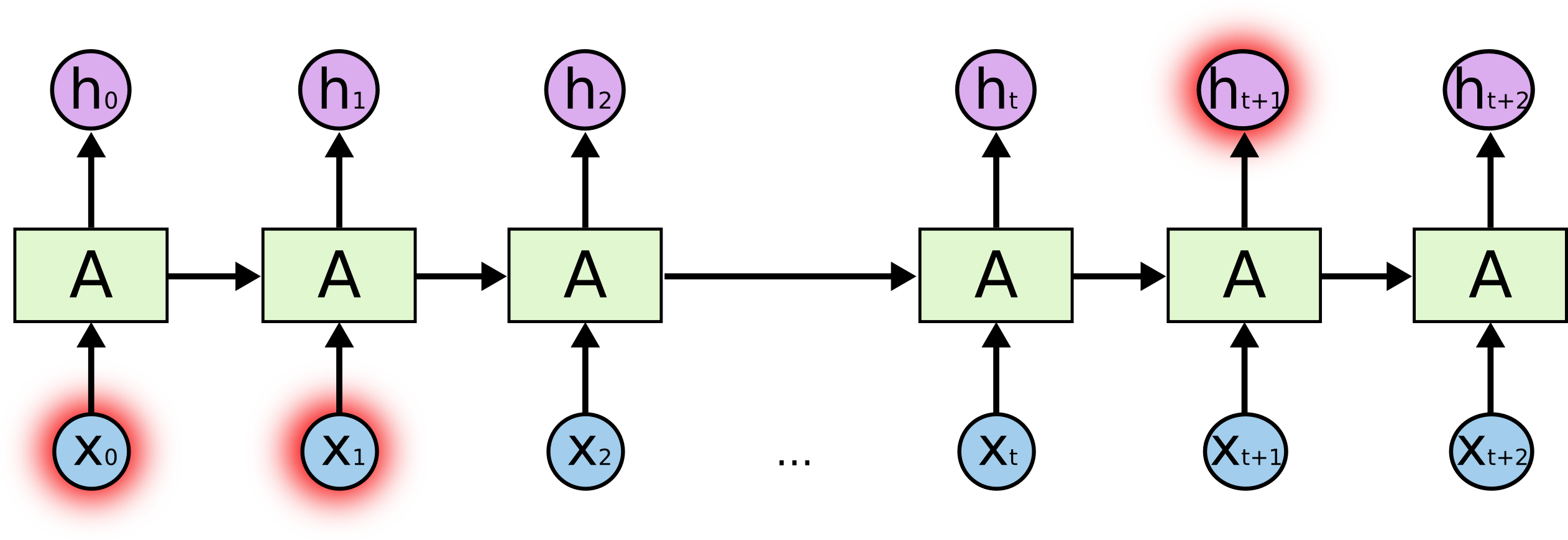
En théorie, les RNN sont absolument capables de gérer de telles « dépendances à long terme ». Un humain pourrait soigneusement choisir des paramètres pour eux afin de résoudre des problèmes de jouets de cette forme. Malheureusement, en pratique, les RNN ne semblent pas être capables de les apprendre. Le problème a été exploré en profondeur par Hochreiter (1991) et Bengio, et al. (1994), qui ont trouvé des raisons assez fondamentales pour lesquelles cela pourrait être difficile.

Heureusement, les LSTM n’ont pas ce problème !

Réseaux LSTM

Les réseaux de mémoire à long terme à court terme – généralement simplement appelés « LSTM » – sont un type spécial de RNN, capable d’apprendre des dépendances à long terme. Ils ont été introduits par Hochreiter & Schmidhuber (1997), et ont été raffinés et popularisés par de nombreuses personnes dans les travaux suivants.1 Ils fonctionnent formidablement bien sur une grande variété de problèmes, et sont maintenant largement utilisés.

LSTMs sont explicitement conçus pour éviter le problème de dépendance à long terme. Se souvenir des informations pendant de longues périodes est pratiquement leur comportement par défaut, et non quelque chose qu’ils luttent pour apprendre !

Tous les réseaux neuronaux récurrents ont la forme d’une chaîne de modules répétitifs de réseau neuronal. Dans les RNN standard, ce module répétitif aura une structure très simple, comme une seule couche tanh.

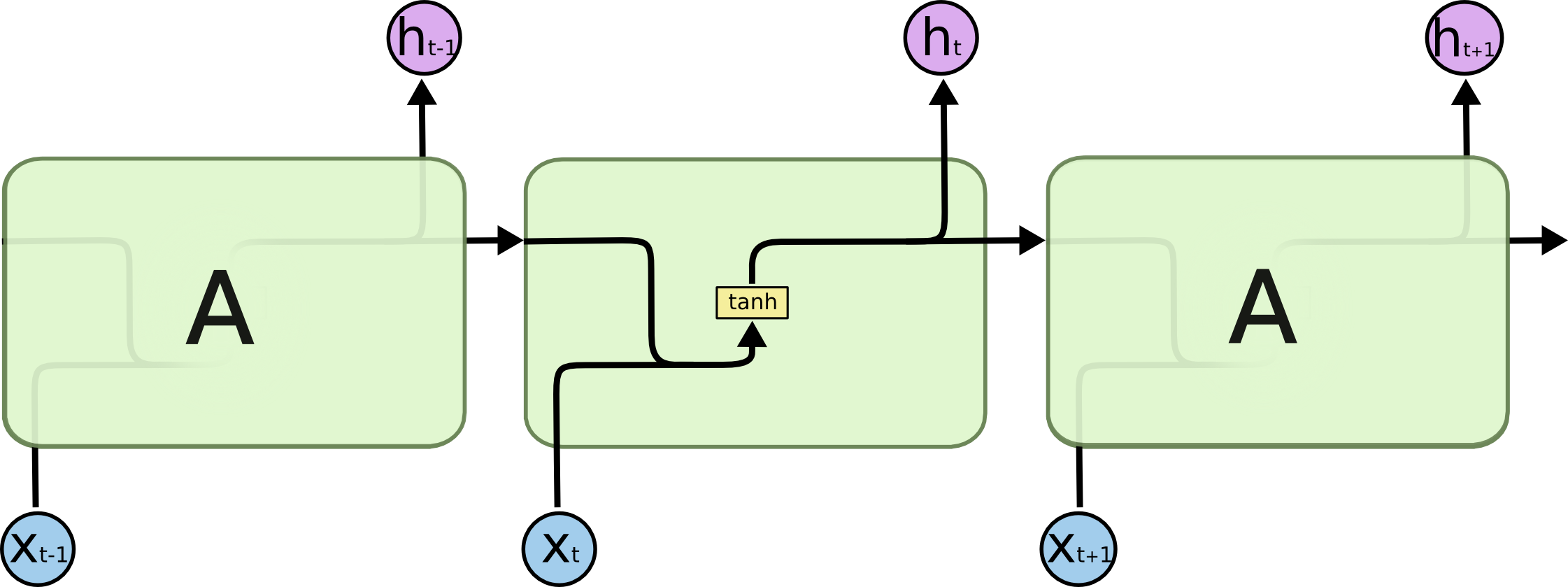
LSTMs ont également cette structure de type chaîne, mais le module répétitif a une structure différente. Au lieu d’avoir une seule couche de réseau neuronal, il y en a quatre, qui interagissent d’une manière très spéciale.

Ne vous inquiétez pas des détails de ce qui se passe. Nous allons parcourir le diagramme LSTM étape par étape plus tard. Pour l’instant, essayons simplement d’être à l’aise avec la notation que nous utiliserons.

Dans le diagramme ci-dessus, chaque ligne porte un vecteur entier, de la sortie d’un nœud aux entrées des autres. Les cercles roses représentent des opérations ponctuelles, comme l’addition de vecteurs, tandis que les boîtes jaunes sont des couches de réseau neuronal apprises. Les lignes qui fusionnent dénotent une concaténation, tandis qu’une ligne qui bifurque dénote que son contenu est copié et que les copies vont à des endroits différents.

L’idée centrale derrière les LSTM

La clé des LSTM est l’état des cellules, la ligne horizontale qui traverse le haut du diagramme.

L’état des cellules est un peu comme un tapis roulant. Il court tout droit le long de la chaîne entière, avec seulement quelques interactions linéaires mineures. Il est très facile pour l’information de simplement s’écouler le long de celui-ci sans changement.

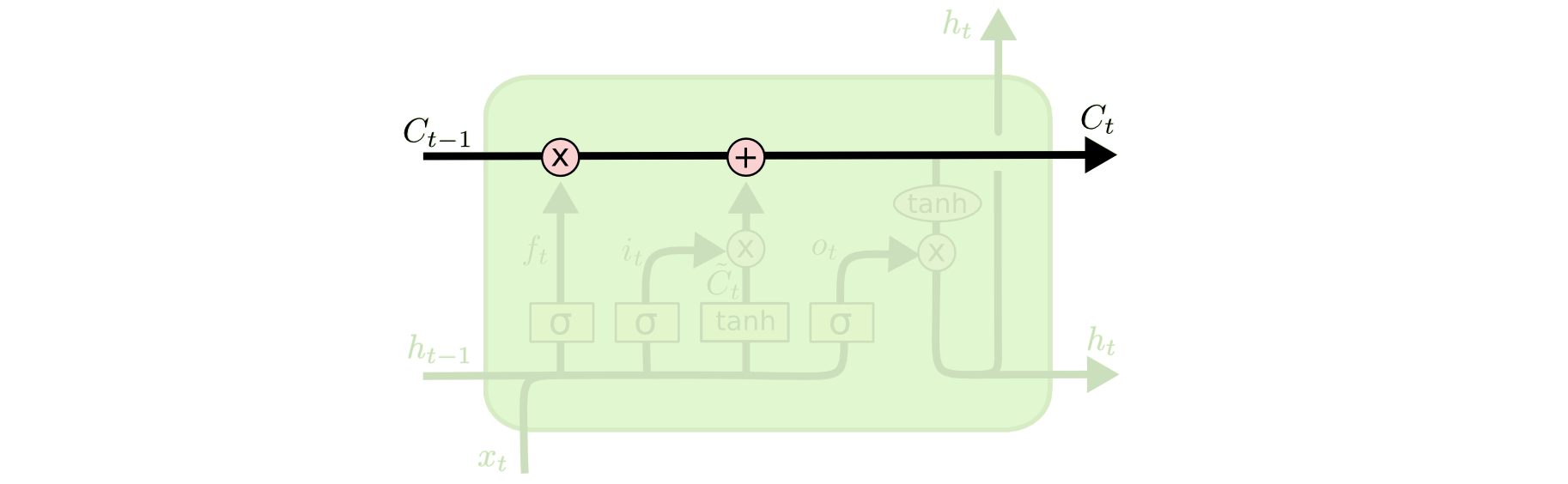
Le LSTM a la capacité de retirer ou d’ajouter des informations à l’état de cellule, soigneusement régulé par des structures appelées portes.

Les portes sont un moyen de laisser optionnellement passer l’information. Elles sont composées d’une couche de réseau neuronal sigmoïde et d’une opération de multiplication par points.

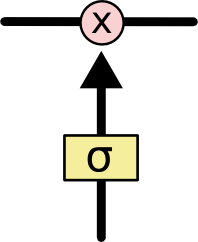
La couche sigmoïde produit des nombres entre zéro et un, décrivant la quantité de chaque composant qui doit être laissé passer. Une valeur de zéro signifie « ne rien laisser passer », tandis qu’une valeur de un signifie « tout laisser passer ! »

Un LSTM possède trois de ces portes, pour protéger et contrôler l’état de la cellule.

Step-by-Step LSTM Walk Through

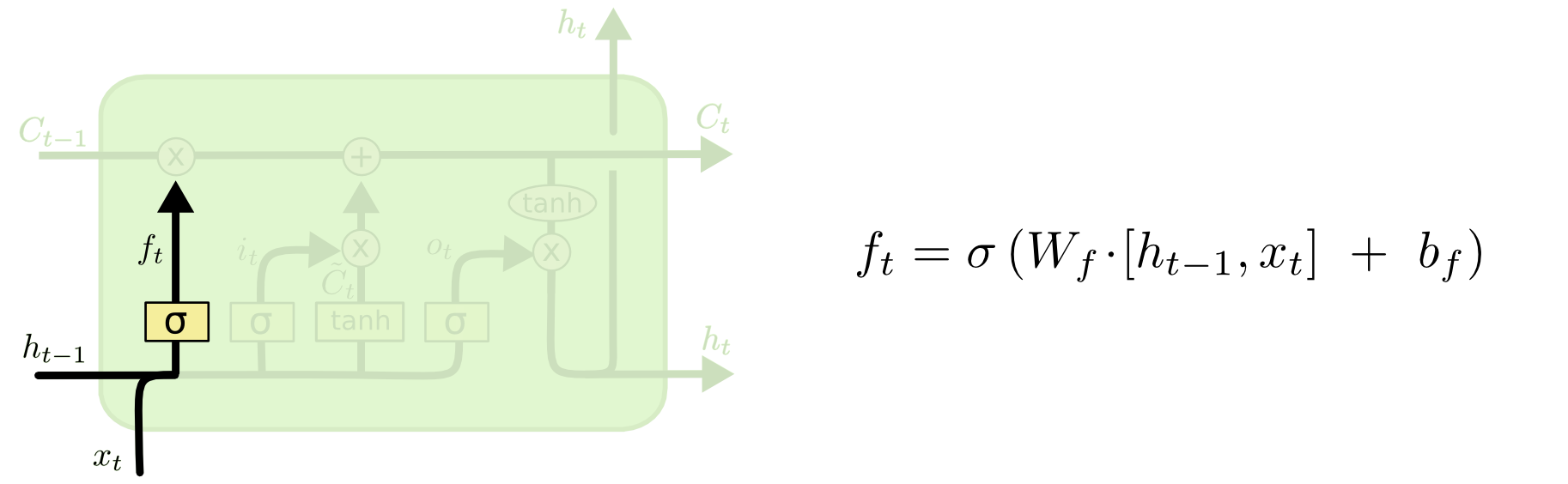
La première étape de notre LSTM consiste à décider quelles informations nous allons jeter de l’état de la cellule. Cette décision est prise par une couche sigmoïde appelée « couche porte d’oubli ». Elle regarde \(h_{t-1}\) et \(x_t\), et sort un nombre entre \(0\) et \(1\) pour chaque nombre dans l’état de la cellule \(C_{t-1}\). Un \(1\) représente « garder complètement ceci » tandis qu’un \(0\) représente « se débarrasser complètement de ceci. »

Revenons à notre exemple d’un modèle de langage essayant de prédire le prochain mot en fonction de tous les précédents. Dans un tel problème, l’état de la cellule pourrait inclure le genre du sujet actuel, afin que les pronoms corrects puissent être utilisés. Lorsque nous voyons un nouveau sujet, nous voulons oublier le genre de l’ancien sujet.

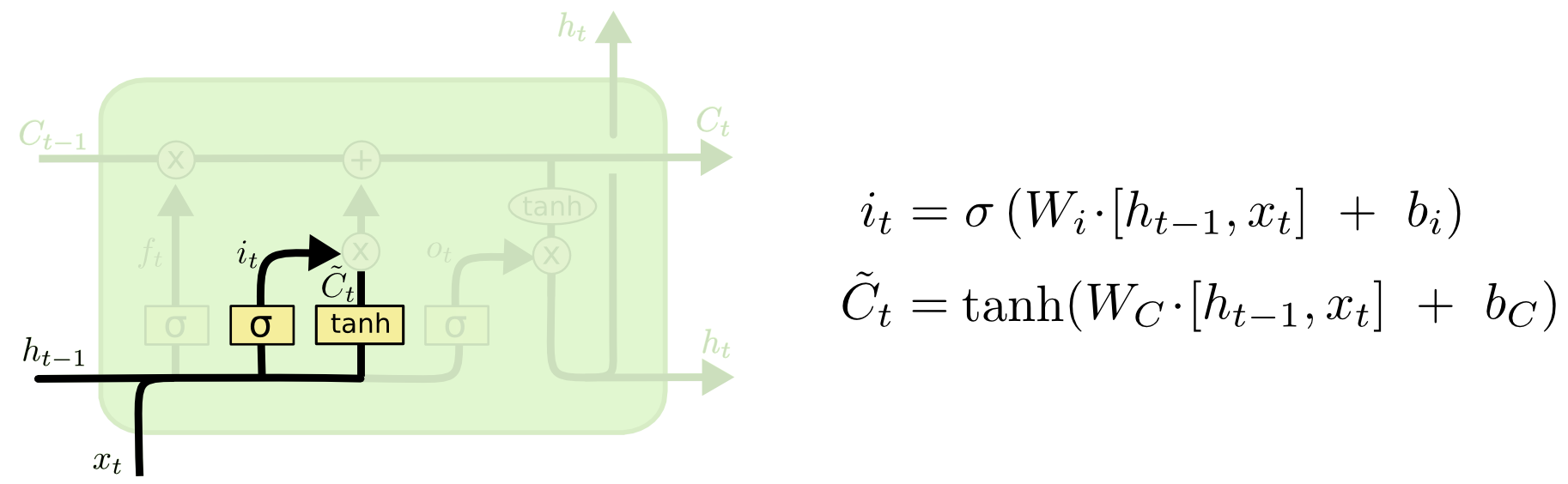
L’étape suivante consiste à décider quelles nouvelles informations nous allons stocker dans l’état cellulaire. Cela comporte deux parties . D’abord, une couche sigmoïde appelée « couche porte d’entrée » décide des valeurs que nous allons mettre à jour. Ensuite, une couche tanh crée un vecteur de nouvelles valeurs candidates, \(\tilde{C}_t\), qui pourraient être ajoutées à l’état. Dans l’étape suivante, nous combinerons les deux pour créer une mise à jour de l’état.

Dans l’exemple de notre modèle de langage, nous voudrions ajouter le sexe du nouveau sujet à l’état de la cellule, pour remplacer l’ancien que nous oublions.

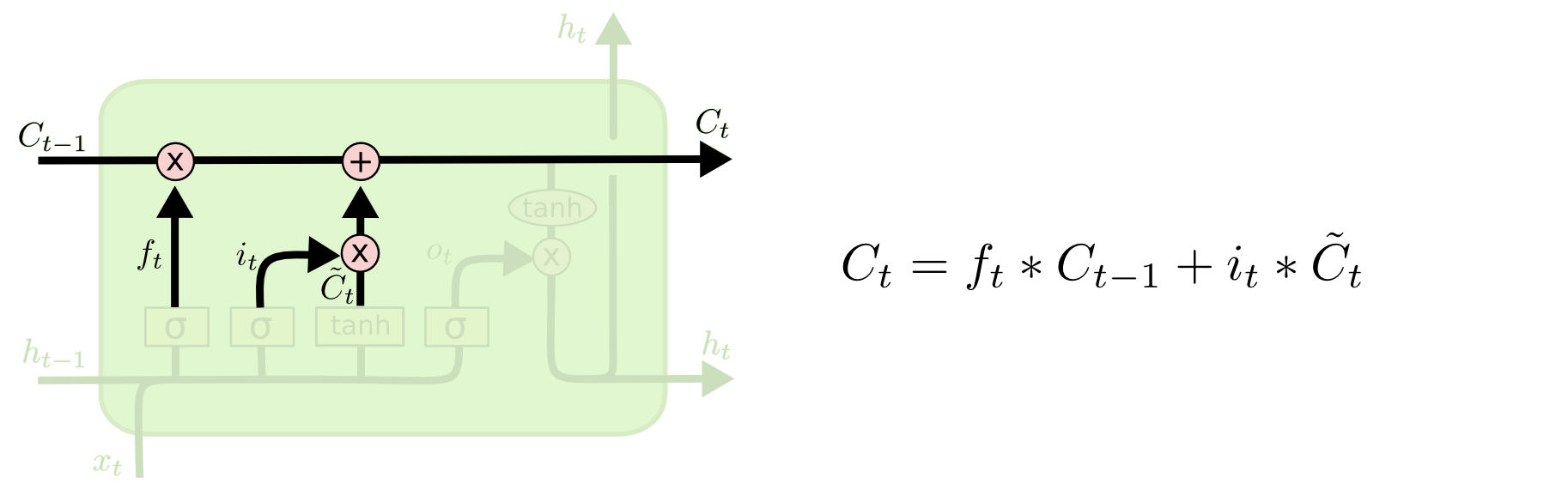
Il est maintenant temps de mettre à jour l’ancien état de la cellule, \(C_{t-1}\), dans le nouvel état de la cellule \(C_t\). Les étapes précédentes ont déjà décidé de ce qu’il faut faire, nous devons juste le faire réellement.

Nous multiplions l’ancien état par \(f_t\), en oubliant les choses que nous avons décidé d’oublier plus tôt. Puis nous ajoutons \(i_t*\tilde{C}_t\). Il s’agit des nouvelles valeurs candidates, mises à l’échelle par combien nous avons décidé de mettre à jour chaque valeur d’état.

Dans le cas du modèle de langage, c’est ici que nous laisserions effectivement tomber l’information sur le sexe de l’ancien sujet et ajouterions la nouvelle information, comme nous l’avons décidé dans les étapes précédentes.

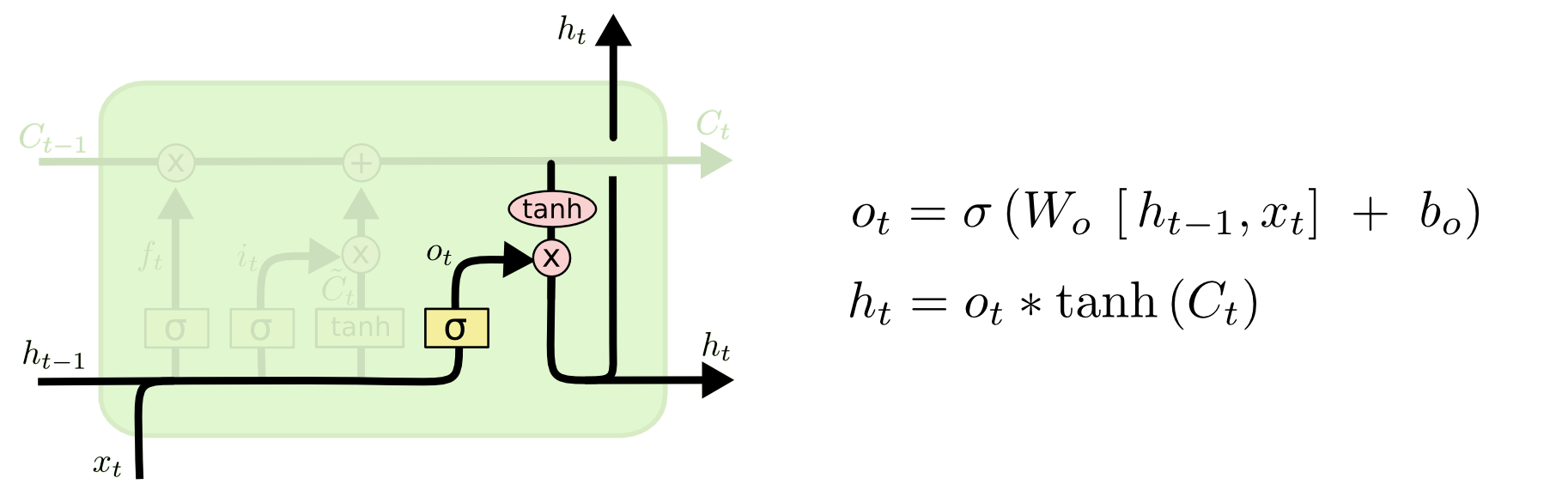
Enfin, nous devons décider ce que nous allons sortir. Cette sortie sera basée sur l’état de notre cellule, mais sera une version filtrée. D’abord, nous exécutons une couche sigmoïde qui décide des parties de l’état cellulaire que nous allons sortir. Ensuite, nous faisons passer l’état de la cellule par \(\tanh\) (pour pousser les valeurs à être entre \(-1\) et \(1\)) et nous le multiplions par la sortie de la porte sigmoïde, de sorte que nous ne sortons que les parties que nous avons décidées.

Pour l’exemple du modèle de langage, puisqu’il vient de voir un sujet, il pourrait vouloir sortir des informations pertinentes pour un verbe, au cas où c’est ce qui vient ensuite. Par exemple, il pourrait sortir si le sujet est singulier ou pluriel, afin que nous sachions sous quelle forme un verbe doit être conjugué si c’est ce qui suit.

Variantes de la mémoire à long court terme

Ce que j’ai décrit jusqu’à présent est un LSTM assez normal. Mais tous les LSTM ne sont pas identiques à ce qui précède. En fait, il semble que presque chaque article impliquant les LSTM utilise une version légèrement différente. Les différences sont mineures, mais il vaut la peine de mentionner certaines d’entre elles.

Une variante populaire de LSTM, introduite par Gers & Schmidhuber (2000), consiste à ajouter des « connexions de type peephole. » Cela signifie que nous laissons les couches de portes regarder l’état de la cellule.

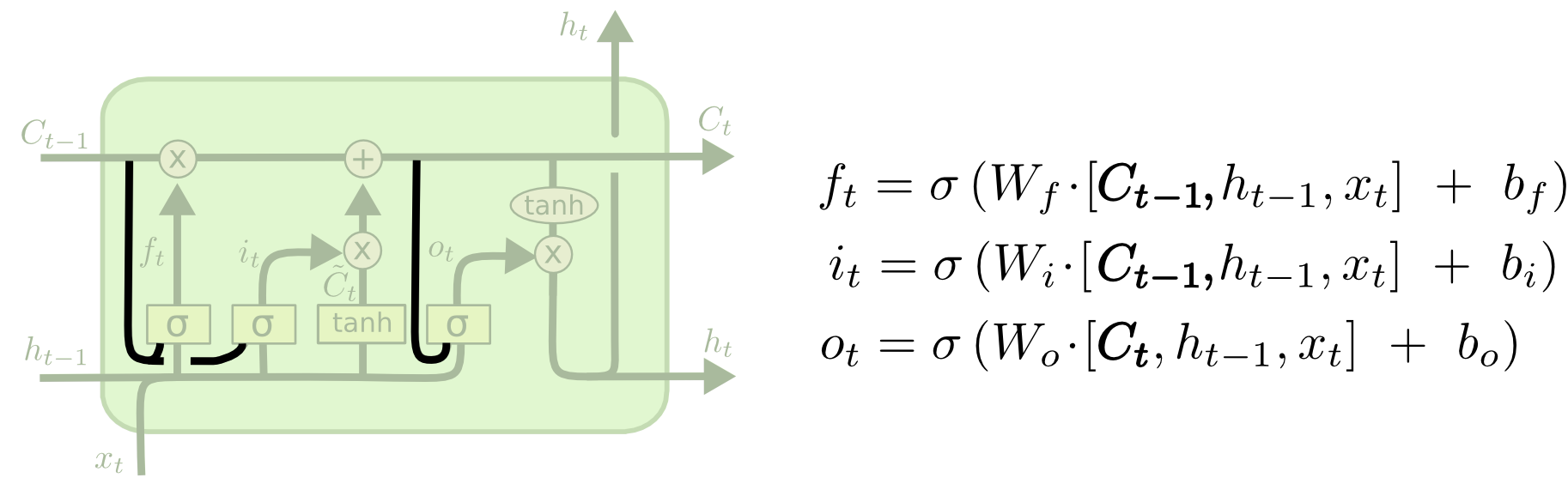
Le diagramme ci-dessus ajoute des peepholes à toutes les portes, mais de nombreux articles donneront certains peepholes et pas d’autres.

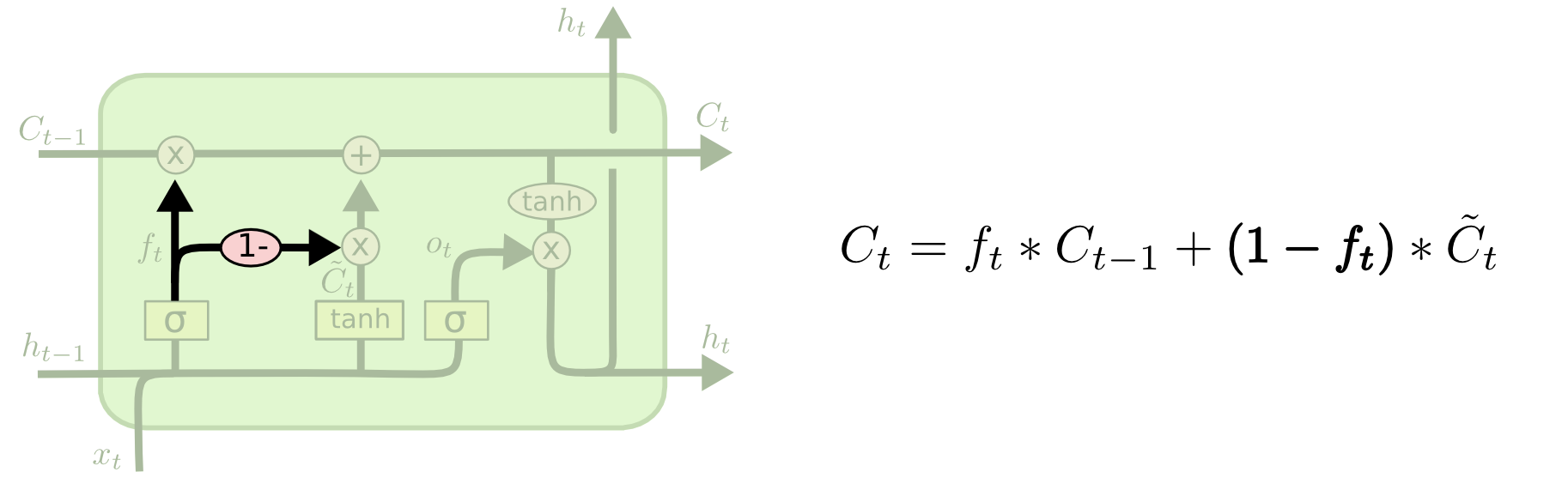
Une autre variation consiste à utiliser des portes d’oubli et d’entrée couplées. Au lieu de décider séparément ce qu’il faut oublier et ce à quoi nous devons ajouter de nouvelles informations, nous prenons ces décisions ensemble. Nous n’oublions que lorsque nous allons entrer quelque chose à sa place. Nous n’entrons de nouvelles valeurs dans l’état que lorsque nous oublions quelque chose d’ancien.

Une variation légèrement plus spectaculaire du LSTM est l’unité récurrente à grille, ou GRU, introduite par Cho, et al. (2014). Elle combine les portes d’oubli et d’entrée en une seule « porte de mise à jour ». Il fusionne également l’état de la cellule et l’état caché, et apporte quelques autres modifications. Le modèle résultant est plus simple que les modèles LSTM standard, et a gagné en popularité.

Ce ne sont que quelques-unes des variantes de LSTM les plus notables. Il y en a beaucoup d’autres, comme les Depth Gated RNNs de Yao, et al. (2015). Il y a aussi une approche complètement différente pour aborder les dépendances à long terme, comme Clockwork RNNs par Koutnik, et al. (2014).

Quelle est la meilleure de ces variantes ? Les différences ont-elles de l’importance ? Greff, et al. (2015) font une belle comparaison des variantes populaires, trouvant qu’elles sont toutes à peu près les mêmes. Jozefowicz, et al. (2015) ont testé plus de dix mille architectures RNN, trouvant certaines qui fonctionnaient mieux que les LSTM sur certaines tâches.

Conclusion

Auparavant, j’ai mentionné les résultats remarquables que les gens obtiennent avec les RNN. Essentiellement, tous ces résultats sont obtenus en utilisant les LSTM. Ils fonctionnent vraiment beaucoup mieux pour la plupart des tâches !

Ecrit sous la forme d’un ensemble d’équations, les LSTM ont l’air assez intimidants. Espérons que le fait de les parcourir pas à pas dans cet essai les a rendus un peu plus abordables.

Les LSTM ont été un grand pas dans ce que nous pouvons accomplir avec les RNN. Il est naturel de se demander : y a-t-il un autre grand pas ? Une opinion commune parmi les chercheurs est : « Oui ! Il y a une prochaine étape et c’est l’attention ! » L’idée est de laisser chaque étape d’un RNN choisir les informations à examiner à partir d’une collection plus large d’informations. Par exemple, si vous utilisez un RNN pour créer une légende décrivant une image, il pourrait choisir une partie de l’image à examiner pour chaque mot qu’il produit. En fait, c’est exactement ce que font Xu et al. (2015). Cela pourrait être un point de départ intéressant si vous voulez explorer l’attention ! Il y a eu un certain nombre de résultats vraiment passionnants en utilisant l’attention, et il semble que beaucoup d’autres sont au coin de la rue…

L’attention n’est pas le seul fil conducteur passionnant dans la recherche RNN. Par exemple, les LSTM de grille de Kalchbrenner, et al. (2015) semblent extrêmement prometteurs. Les travaux utilisant les RNN dans les modèles génératifs – comme Gregor, et al. (2015), Chung, et al. (2015), ou Bayer &Osendorfer (2015) – semblent également très intéressants. Les dernières années ont été une période passionnante pour les réseaux de neurones récurrents, et celles à venir promettent de ne l’être que davantage !

Remerciements

Je suis reconnaissant à un certain nombre de personnes qui m’ont aidé à mieux comprendre les LSTM, à commenter les visualisations et à fournir des commentaires sur ce billet.

Je suis très reconnaissant à mes collègues de Google pour leurs commentaires utiles, en particulier Oriol Vinyals, Greg Corrado, Jon Shlens, Luke Vilnis et Ilya Sutskever. Je suis également reconnaissant envers de nombreux autres amis et collègues qui ont pris le temps de m’aider, notamment Dario Amodei et Jacob Steinhardt. Je suis particulièrement reconnaissant à Kyunghyun Cho pour une correspondance extrêmement réfléchie sur mes diagrammes.

Avant ce post, je me suis exercé à expliquer les LSTM au cours de deux séries de séminaires que j’ai enseignés sur les réseaux neuronaux. Merci à tous ceux qui y ont participé pour leur patience avec moi, et pour leurs commentaires.

1. En plus des auteurs originaux, beaucoup de gens ont contribué au LSTM moderne. Une liste non exhaustive est : Felix Gers, Fred Cummins, Santiago Fernandez, Justin Bayer, Daan Wierstra, Julian Togelius, Faustino Gomez, Matteo Gagliolo et Alex Graves.

Plus de messages

.