Tableau des arctangentes
| y | x = arctan(y) | |
|---|---|---|
| degrés | radians | |
| -1.732050808 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -0.577350269 | -30° | -π/6 |
| 0 | 0° | 0 |
| 0.577350269 | 30° | π/6 |
| 1 | 45° | π/4 |
| 1.732050808 | 60° | π/3 |
Quel est l’arctangente de 0 ?
arctan 0 = ?
L’arctangente est la fonction tangente inverse.
Puisque, tan 0 = tan 0º = 0
L’arctangente de 0 est égale à la fonction tangente inverse de 0, qui est égale à 0 radians ou 0 degrés :
arctane 0 = tan-1 0 = 0 rad = 0º
Quelle est l’arctangente de 1 ?
arctan 1 = ?
L’arctangente est la fonction tangente inverse.
Puisque, tan π/4 = tan 45º = 1
L’arctangente de 1 est égale à la fonction tangente inverse de 1, qui est égale à π/4 radians ou 45 degrés :
arctan 1 = tan-1 1 = π/4 rad = 45º
Quel est l’arctangente de 2 ?
arctangente de 2 = ?
L’arctangente est la fonction tangente inverse.
Puisque, tan 1,107 = tan 63,435º = 2
L’arctangente de 2 est égale à la fonction tangente inverse de 2, qui est égale à 1.107 radians ou 63,435 degrés:
arctangente de 2 = tan-1 2 = 1,107 rad = 63,435º
Arctangente de l’infini
Quel est l’arctangente de l’infini et de moins l’infini ?
arctan(∞) = ?
L’arctangente est la fonction tangente inverse.
La limite de l’arctangente de x lorsque x s’approche de l’infini est égale à pi/2 radians ou 90 degrés:
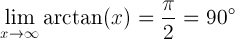
La limite de l’arctangente de x lorsque x s’approche de moins l’infini est égale à -pi/2 radians ou -90 degrés:
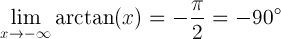
Dérivée de l’arctan
Quelle est la dérivée de la fonction arctangente de x ?
La dérivée de la fonction arctangente de x est égale à 1 divisé par (1+x2)
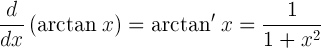
Intégrale de arctan
Qu’est-ce que l’intégrale de la fonction arctangente de x ?
L’intégrale indéfinie de la fonction arctangente de x est:

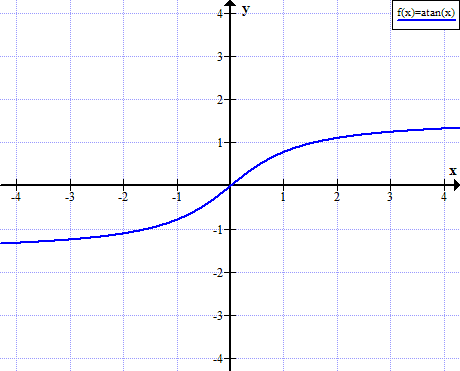
Graphe d’arctan
Graphe d’arctangente de x:
Quel est le sinus d’arctan(x)
sin( arctan(x) ) = ?
Le sinus de l’arctangente de x est:
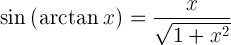
Quel est le cosinus de arctan(x)
cos( arctan(x) ) = ?
Le cosinus de l’arctangente de x est:
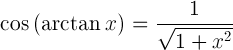 .
.