Statistiques Définitions >Asymétrie du mode de Pearson
L’asymétrie du mode de Pearson, également appelée premier coefficient d’asymétrie de Pearson, est un moyen de déterminer l’asymétrie d’une distribution.
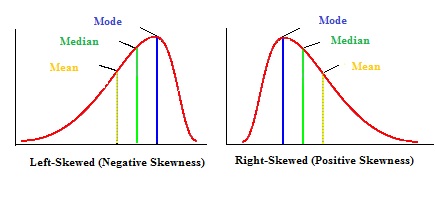
La moyenne, le mode et la médiane peuvent être utilisés pour déterminer si vous avez une distribution positivement ou négativement asymétrique.
- Si la moyenne est supérieure au mode, la distribution est positivement asymétrique.
- Si la moyenne est inférieure au mode, la distribution est négativement asymétrique.
- Si la moyenne est supérieure à la médiane, la distribution est positivement asymétrique.
- Si la moyenne est inférieure à la médiane, la distribution est négativement asymétrique.
Distorsion en mode Pearson
La distorsion en mode Pearson utilise les faits ci-dessus pour vous aider à savoir si vous avez une distorsion positive ou négative. Si vous avez une distribution et que vous connaissez la moyenne, le mode et l’écart-type (σ), alors la formule de l’asymétrie du mode de Pearson est :
(moyenne-mode)/σ
Problématique de l’échantillon : Vous avez des données avec une moyenne de 19, un mode de 20 et un écart-type de 25. Que vous dit l’asymétrie du mode de Pearson à propos de la distribution ?
(moyenne-mode)/σ = (19-20)/25 = -0,04.
Il y a une très légère asymétrie négative (-0,04). Note : Pour la plupart des intentions et des buts, ceci compterait comme une distribution symétrique puisque l’asymétrie est si petite.
Pearson Mode Skewness : Formule alternative.
Si vous ne connaissez pas le mode, vous ne pourrez pas utiliser l’asymétrie du mode Pearson. Cependant, la direction de l’asymétrie peut également être déterminée en trouvant où se trouvent la moyenne et la médiane. Selon Business Statistics, cela conduit à une deuxième formule équivalente :
3(Moyenne – Médiane) / σ
Cette formule est également appelée deuxième coefficient d’asymétrie de Pearson.
Pearson Mode Skewness : Ce que signifient les résultats.
La différence entre la moyenne et le mode, ou la moyenne et la médiane, vous indique dans quelle mesure la distribution s’écarte de la symétrie. Une distribution symétrique (par exemple, la distribution normale) a une asymétrie de zéro.
Les deux équations vous donnent des résultats en écarts types, qui sont des unités de mesure sans dimension par rapport à la moyenne.
Dodge, Y. (2008). L’encyclopédie concise de la statistique. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). L’introduction aux statistiques en bandes dessinées. Hill & Wamg.
Vogt, W.P. (2005). Dictionnaire de la statistique &Méthodologie : Un guide non technique pour les sciences sociales. SAGE.
Stephanie Glen. « Mode de Pearson Skewness » De StatisticsHowTo.com : Des statistiques élémentaires pour le reste d’entre nous ! https://www.statisticshowto.com/pearson-mode-skewness/
——————————————————————————
Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert dans le domaine. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !