Algèbre matricielle

Nous allons décrire trois exemples issus des sciences de la vie : un de la physique, un lié à la génétique et un autre d’une expérience sur des souris. Ils sont très différents, et pourtant nous finissons par utiliser la même technique statistique : l’ajustement de modèles linéaires. Les modèles linéaires sont généralement enseignés et décrits dans le langage de l’algèbre matricielle.

Exemples motivants

Objets tombants

Imaginez que vous êtes Galilée au 16ème siècle et que vous essayez de décrire la vitesse d’un objet tombant. Un assistant grimpe sur la Tour de Pise et laisse tomber une balle, tandis que plusieurs autres assistants enregistrent la position à différents moments. Simulons quelques données en utilisant les équations que nous connaissons aujourd’hui et en ajoutant une erreur de mesure:

set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##meters

Les assistants remettent les données à Galilée et voici ce qu’il voit:

mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")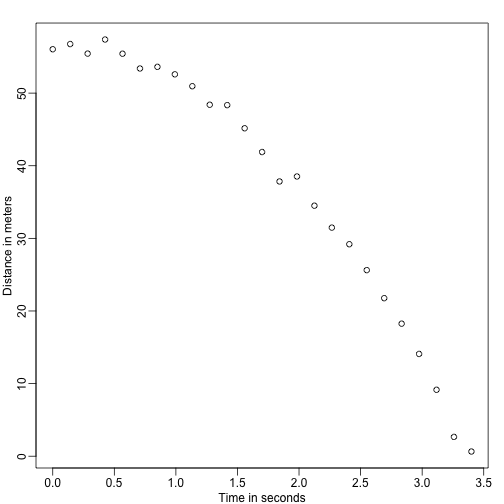

Il ne connaît pas l’équation exacte, mais en regardant le tracé ci-dessus, il déduit que la position doit suivre une parabole. Il modélise donc les données avec :

Avec représentant la position, représentant le temps, et tenant compte de l’erreur de mesure. C’est un modèle linéaire parce que c’est une combinaison linéaire de quantités connues (th s) appelées prédicteurs ou covariables et de paramètres inconnus (les s).

Hauteurs père & fils

Maintenant, imaginez que vous êtes Francis Galton au 19ème siècle et que vous collectez des données de taille appariées de pères et de fils. Vous soupçonnez que la taille est héritée. Vos données:

library(UsingR)x=father.son$fheighty=father.son$sheight

semblent à ceci:

plot(x,y,xlab="Father's height",ylab="Son's height")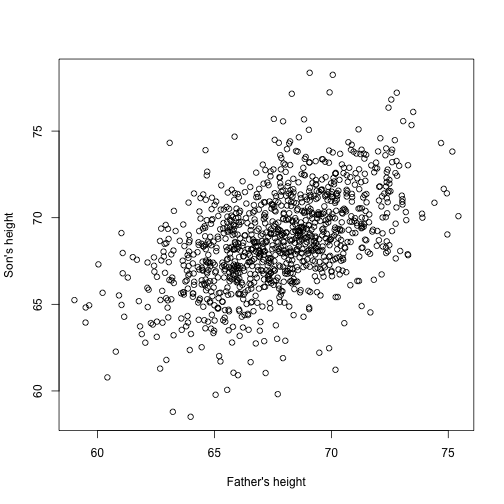

La taille des fils semble effectivement augmenter linéairement avec celle des pères. Dans ce cas, un modèle qui décrit les données est le suivant :

C’est aussi un modèle linéaire avec et , les hauteurs des pères et des fils respectivement, pour la -ième paire et un terme pour tenir compte de la variabilité supplémentaire. Ici, nous pensons que les hauteurs des pères sont le prédicteur et qu’elles sont fixes (et non aléatoires), c’est pourquoi nous utilisons des minuscules. L’erreur de mesure seule ne peut pas expliquer toute la variabilité observée dans . Cela est logique car il y a d’autres variables qui ne sont pas dans le modèle, par exemple, les hauteurs des mères, le hasard génétique et les facteurs environnementaux.

Échantillons aléatoires de plusieurs populations

Nous lisons ici les données de poids corporel de souris qui ont été nourries avec deux régimes différents : riche en graisses et contrôle (chow). Nous avons un échantillon aléatoire de 12 souris pour chacun. Nous sommes intéressés à déterminer si le régime alimentaire a un effet sur le poids. Voici les données:

dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")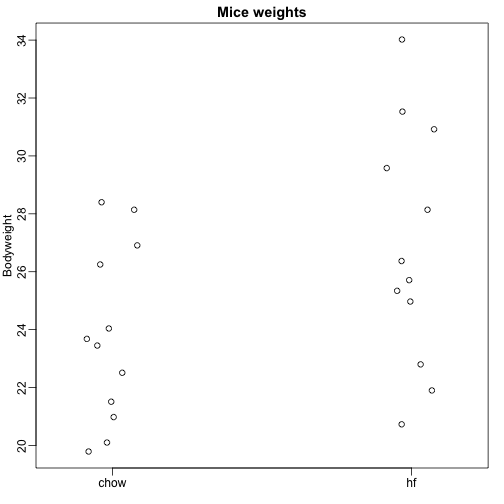

Nous voulons estimer la différence de poids moyen entre les populations. Nous avons montré comment le faire en utilisant des tests t et des intervalles de confiance, basés sur la différence entre les moyennes des échantillons. Nous pouvons obtenir exactement les mêmes résultats en utilisant un modèle linéaire :

avec le poids moyen du régime chow, la différence entre les moyennes, quand la souris reçoit le régime riche en graisses (hf), quand elle reçoit le régime chow, et explique les différences entre les souris de la même population.

Modèles linéaires en général

Nous avons vu trois exemples très différents dans lesquels les modèles linéaires peuvent être utilisés. Un modèle général qui englobe tous les exemples ci-dessus est le suivant :

Notez que nous avons un nombre général de prédicteurs . L’algèbre matricielle fournit un langage compact et un cadre mathématique pour calculer et faire des dérivations avec n’importe quel modèle linéaire qui s’insère dans le cadre ci-dessus.

Estimation des paramètres

Pour que les modèles ci-dessus soient utiles, nous devons estimer les s inconnus. Dans le premier exemple, nous voulons décrire un processus physique pour lequel nous ne pouvons pas avoir de paramètres inconnus. Dans le deuxième exemple, nous comprenons mieux l’héritage en estimant dans quelle mesure, en moyenne, la taille du père affecte la taille du fils. Dans le dernier exemple, nous voulons déterminer s’il existe effectivement une différence : si .

L’approche standard en science consiste à trouver les valeurs qui minimisent la distance du modèle ajusté aux données. Ce qui suit est appelé l’équation des moindres carrés (LS) et nous la verrons souvent dans ce chapitre :

Une fois que nous avons trouvé le minimum, nous appellerons les valeurs les estimations des moindres carrés (LSE) et les désignerons par . La quantité obtenue en évaluant l’équation des moindres carrés aux estimations est appelée la somme résiduelle des carrés (RSS). Comme toutes ces quantités dépendent de , elles sont des variables aléatoires. Les s sont des variables aléatoires et nous finirons par effectuer des inférences sur elles.

Exemple de l’objet tombant revisité

Grâce à mon professeur de physique du lycée, je sais que l’équation de la trajectoire d’un objet tombant est :

avec et la hauteur et la vitesse de départ respectivement. Les données que nous avons simulées ci-dessus ont suivi cette équation et ont ajouté une erreur de mesure pour simuler nles observations de la chute de la balle depuis la tour de Pise . C’est pourquoi nous avons utilisé ce code pour simuler les données:

g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)

Voici à quoi ressemblent les données avec la ligne solide représentant la vraie trajectoire:

plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)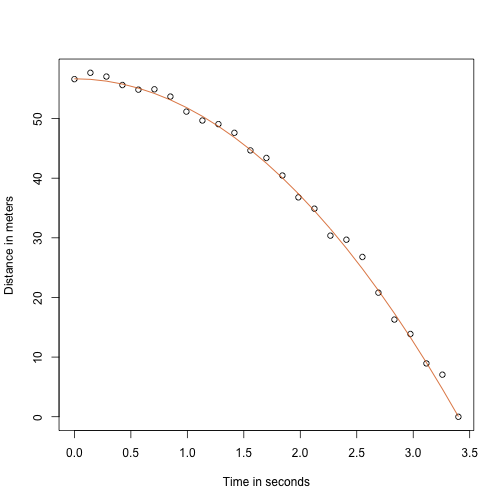

Mais nous faisions semblant d’être Galilée et donc nous ne connaissons pas les paramètres du modèle. Les données suggèrent bien qu’il s’agit d’une parabole, donc nous la modélisons comme telle :

Comment trouver le LSE ?

La fonction lm

Dans R, nous pouvons ajuster ce modèle en utilisant simplement la fonction lm. Nous décrirons cette fonction en détail plus tard, mais voici un aperçu:

tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef

## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17

Elle nous donne le LSE, ainsi que les erreurs standard et les valeurs p.

Une partie de ce que nous faisons dans cette section est d’expliquer les mathématiques derrière cette fonction.

L’estimation des moindres carrés (LSE)

Ecrivons une fonction qui calcule le RSS pour tout vecteur :

rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}

Donc pour tout vecteur tridimensionnel nous obtenons un RSS. Voici un graphique du RSS en fonction du moment où nous gardons les deux autres fixes:

Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)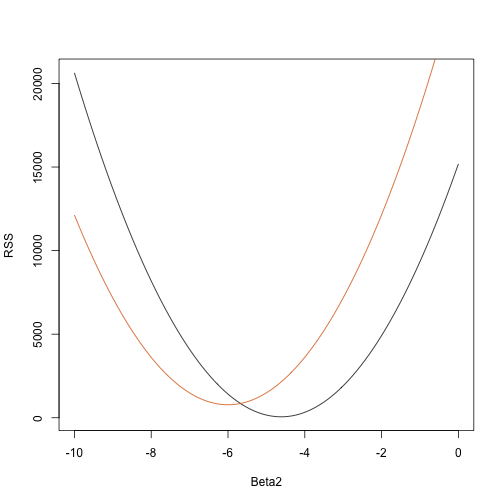

Les essais et erreurs ici ne vont pas fonctionner. Au lieu de cela, nous pouvons utiliser le calcul : prendre les dérivées partielles, les mettre à 0 et résoudre. Bien sûr, si nous avons de nombreux paramètres, ces équations peuvent devenir assez complexes. L’algèbre linéaire fournit un moyen compact et général de résoudre ce problème.

Plus sur Galton (avancé)

En étudiant les données père-fils, Galton a fait une découverte fascinante en utilisant l’analyse exploratoire.

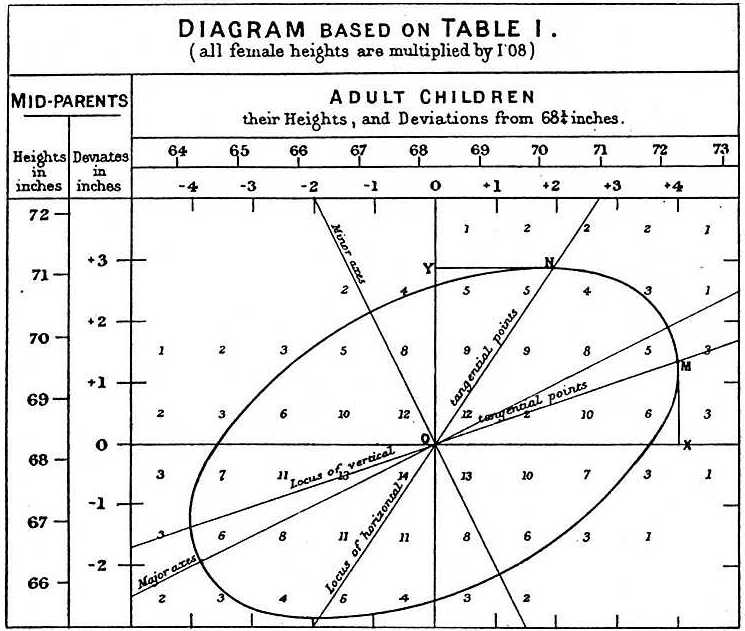
Il a remarqué que s’il tabulait le nombre de paires de taille père-fils et suivait toutes les valeurs x,y ayant les mêmes totaux dans le tableau, elles formaient une ellipse. Dans le graphique ci-dessus, réalisé par Galton, vous voyez l’ellipse formée par les paires ayant 3 cas. Cela a ensuite conduit à modéliser ces données comme une normale bivariée corrélée que nous avons décrite précédemment :

Nous avons décrit comment nous pouvons utiliser les mathématiques pour montrer que si vous gardez fixe (condition d’être ) la distribution de est normalement distribuée avec une moyenne : et un écart-type . Notez que est la corrélation entre et , ce qui implique que si nous fixons , suit en fait un modèle linéaire. Les paramètres et de notre modèle linéaire simple peuvent être exprimés en termes de , et .

.