Nous pouvons utiliser Gibbs-Helmholtz pour obtenir la dépendance en température de \(K\)
\}{∂T}. \right)_P = \dfrac{-Δ_rH^o}{T^2}\]
À l’équilibre, on peut assimiler \(Δ_rG^o\) à \(-RT\ln K\) donc on obtient:
\}{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2}
Nous voyons que le fait que \(K\) augmente ou diminue avec la température est lié au fait que l’enthalpie de réaction est positive ou négative. Si la température est changée suffisamment peu pour que Δ_rH^o\ puisse être considérée comme constante, nous pouvons traduire une valeur de \(K\) à une température en une autre en intégrant l’expression ci-dessus, nous obtenons une dérivation similaire à celle de la dépression du point de fusion :
Si une plus grande précision est requise, nous pourrions corriger les changements de température de ΔrHo en utilisant les données de capacité thermique.
La façon dont \(K\) augmente ou diminue avec la température est liée au fait que l’enthalpie de réaction est positive ou négative.
L’expression de \(K\) est une fonction assez sensible de la température étant donné sa dépendance exponentielle de la différence des coefficients stœchiométriques Une façon de voir la dépendance sensible de la température des constantes d’équilibre est de rappeler que
Cependant, puisque sous pression et température constantes
L’équation \(\ref{18}\) devient
En prenant le log naturel des deux côtés, nous obtenons une relation linéaire entre \(\ln K \)et les enthalpies et entropies standard :
\
qui est connue comme l’équation de van’t Hoff. Elle montre qu’un tracé de \(\ln K\) en fonction de \(1/T\) devrait être une ligne avec une pente \(-\Delta_r{H^o}/R\) et une interception \(\Delta_r{S^o}/R\).
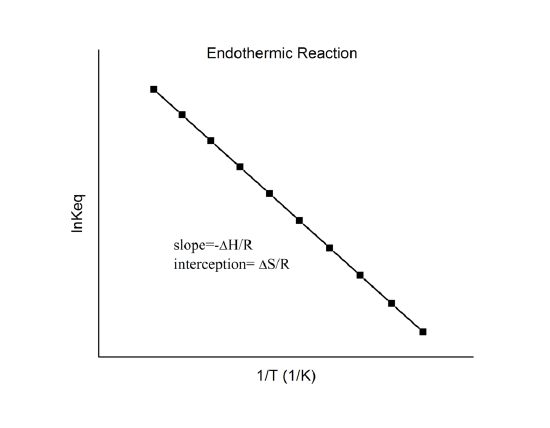
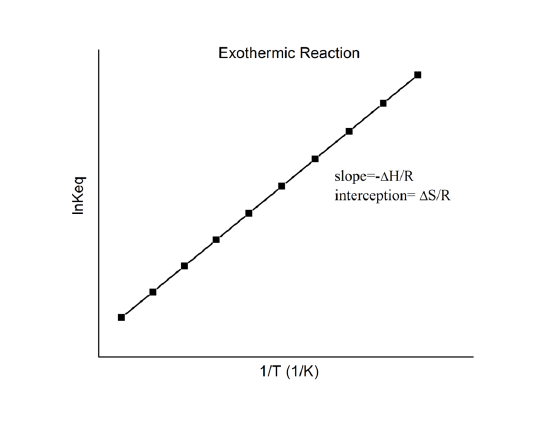
Il est donc possible de déterminer ces quantités à partir des données \(\ln K\) vs. \(1/T\) sans faire de calorimétrie. Bien sûr, la principale hypothèse ici est que \(\Delta_r{H^o}\) et \(\Delta_r{S^o}\) ne dépendent que très faiblement de \(T\), ce qui est généralement valable.
Contributeurs et attributions
.