Huomautus: tämä on Vortex Math -analyysimme ensimmäinen sivu. Klikkaa tästä, jos etsit interaktiivista Vortex-N-k-sovellusta.
Rakas professori Puzzler,
Olen kuullut ihmisten puhuvan ”Vortex-matematiikasta”, ja haluan ymmärtää, mitä se on. Voitteko auttaa?
Mystified in Maine
Dear Mystified,
Hyvin mielelläni autan sinua. Tästä tulee ajoittain hieman teknistä, mutta jotta asia olisi mielenkiintoinen, hyvä ystäväni Marko-11 Wunfishiasta on tarjoutunut tekemään vieraskirjoituksen. Marko-11 on hieman outo (kirjaimellisesti) – hänellä on kymmenen sijasta yksitoista sormea, ja se antaa hänelle aivan uuden näkökulman matematiikkaan. Jos pysyt mukana hänen selityksensä loppuun asti, takaan, että nautit matkasta! Marko?
Kiitos, professori Puzzler. Minun täytyy varoittaa lukijoitasi siitä, että aion tehdä tässä hieman kevyttä numeroteoriaa, mutta jos matematiikka ei ole heidän vahvuutensa, he voivat antaa silmiensä lasittua matematiikkajuttujen aikana ja katsoa vain kommenttiani kauniisiin kuviin.
Aluksi haluaisin varmistaa, että kaikki ystäväsi ymmärtävät, että kaikki eivät laske kuten he. Useimmat ystäväsi laskevat luultavasti numerojärjestelmässä nimeltä peruskymppi, jossa on seuraavat numerot: 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9. Se ei ole epätavallista, koska heillä kaikilla on kymmenen sormea. Minä taas lasken (niin sanotusti) yhdellätoista (voit varmaan arvata miksi). Laskentajärjestelmässäni on ylimääräinen numero, aivan kuten minullakin on ylimääräinen numero. Minun numeroni ovat 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ja A. ”A”? Saatat sanoa: ”Se on kirjain, ei numero!” Totta, totta, mutta aina kun työskennellään kymmentä suuremmalla emäksellä, tarvitaan lisänumeroita, ja sen sijaan, että keksisimme uusia symboleja, otamme vain käyttöön symbolit, joita ei käytetä mihinkään muuhun (pahoittelut ystäviltäni englanninopettajilta!)
Nyt, koska teen aritmeettisia laskutoimituksia emäksellä yksitoista, kirjoitan numerot hyvin eri tavalla. Esimerkiksi kun haluan kirjoittaa luvun 34, kirjoitan ”31”. Miksi? Koska se tarkoittaa ”3 yksitoista plus 1 lisää”. Luvun 87 kirjoitan ”7A”, koska 7 yksitoista plus A (se on numerosi 10) on 87.
Teen siis hienoja aritmeettisia laskutoimituksia, ja kaikki tapahtuu perusyhtätoista, joten sinun on seurattava tarkasti, jotta voit seurata minua.

Ensin piirrän ympyrän ja merkitsen kaikki numerot ympyrän kehälle. No, oikeastaan en kaikkia; jätän nollan väliin. Älkää kysykö miksi; en ole varma, onko minulla oikeastaan hyvää syytä, mutta se saa kaiken tulemaan oikein. Luota siis minuun. Minulla on yksitoista sormea, joten miten voisin olla väärässä?
Nyt kun olen piirtänyt ympyrän, alan yhdistää numeroita seuraavalla tavalla. Aloitan numerosta 2 ja tuplaan sen. Tulos on 4. Yhdistän siis 2 ja 4. Nyt tuplaan 4. Tuloksena on 8, joten yhdistän 4 ja 8. Nyt tuplaan 8, ja se on… oho… se on 15. (Tiedän, mitä ajattelet – se on 16.) Mutta se on kymmensormijärjestelmä. Perusyksikössä yksitoista, 16 kirjoitetaan 15, koska 1 yksitoista plus 5 lisää on 16).
Hienoa, mutta minulla ei ole numeroa 15. Ei se haittaa… Lasken vain yhteen 1 ja 5, jotta saan 6, ja sitten yhdistän 8 ja 6. Nyt tuplaan 15 (perusyksikkö yksitoista) ja saan 2A (se on 32 sinulle!). Nyt lisään numerot 2 + A = 11 (perusyhtätoista). Koska minulla ei ole numeroa 11, lasken numerot yhteen: 1 + 1 = 2, joten vedän viivan, joka yhdistää 6 ja 2.

Vau! Tuo näyttää todella siistiltä! Se on kuin kaunis äärettömyyssymboli, joka on maailmankaikkeuden tapa kertoa minulle, että olen löytämässä jotain aivan erityistä, joka johtaa äärettömään kaikkeen kaikille!
Tehdäkseni siitä vielä mielenkiintoisemman, jos tuplaan 2A:n ja teen kartoitusprosessini, se kartoittaa 4:ää, ja seuraava tuplaus kartoittaa 8:aa, sitten 6:aa, ja se toistuu uudestaan ja uudestaan ja uudestaan, mikä on tietysti symboli loputtomasta rikkaudesta, joka odottaa minua, kunhan myyn tämän idean muille wunfishilaisille!
Mutta entäpä raukat pikkuiset pikku kolmoset 3, viisi, seitsemän, yhdeksän ja A? Mitä ne kuvaavat? Tästä tulee TODELLA siistiä; 1 kartoittaa 2:n, 3:n 6:n, 5:n A:n, 7:n 4:n ja 9:n 8:n. Toisin sanoen, lukuun ottamatta 5:tä, ne kaikki syöttävät suoraan äärettömyyden kiertokulkuun, antaen minulle vielä enemmän sitä ääretöntä energiaa, vaurautta ja syöväntorjuntapotentiaalia, jonka olen jo löytänyt. Mitä? Enkö kertonut sinulle syövän torjumisesta? Kerroin. Se on itsestäänselvyys.
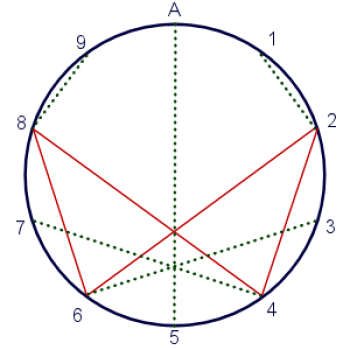
Ja mihin A liittyy? Se on hämmästyttävä juttu; A kartoittaa ITSENSÄ. Ei ole väliä kuinka monta kertaa sitä tuplataan, A vain jatkaa itsensä kartoittamista. Tämä kertoo minulle, että A (numerosi 10) on maaginen vakio, joka hallitsee maailmankaikkeutta ja sitoo yhteen matematiikan jumalallisen kielen.
Todellisuudessa tämä koko juttu näyttäisi paljon siistimmältä, jos sen sijaan, että kartoittaisin 1, 3, 7 ja 9 äärettömään silmukkaan, kartoittaisin ne maagiseen lukuuni. Älä kysy miksi – en tarvitse syytä. Se vain näyttää siistiltä, joten teen niin.
Nyt pyörrekaavioni näyttää äärettömyydeltä joulukuusen alla, mikä on maailmankaikkeuden tapa kertoa minulle, että tämä on sen lahja minulle.
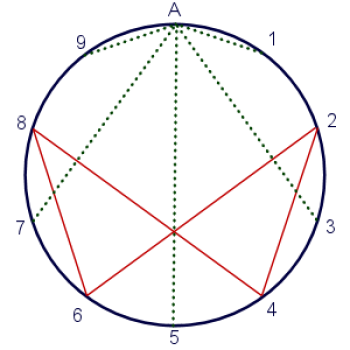
Ei suinkaan. En näet keksinyt Vortex-matematiikkaa. Sen keksi eräs raukka (kutsun häntä mielelläni Marko-10:ksi), jolla oli valitettavasti vain 10 sormea. Ja koska hänellä oli vain 10 sormea, hän teki sen surullisen virheen, että hän yritti tehdä kaiken tämän kymmensormisena.
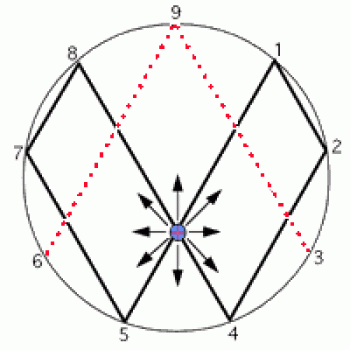
Tietenkään hänen pyörrekaavionsa ei ollut yhtä kaunis kuin minun. Huomaa, että hänen äärettömyyssymbolinsa on paljon vähemmän tyylikäs kuin omani, ja se vaatii ylimääräistä kaksinkertaistamista palataksemme takaisin äärettömään hyvyyteen. Huomaa myös, että hän ei oikein tiennyt mitä tehdä pikku 3 ja 6 -raukoille, jotka snobisti vain kartoittavat edestakaisin toisiaan, eivätkä ruoki hänen ääretöntä energiavarastoaan.
Ja onko hänen joulukuusessaan edes runkoa? Ei, ei ole. Ja oksia on vain yksi sarja, joten maailmankaikkeuteen ei mahdu montaakaan lahjaa tuon kuusen alle.
Mikä on tuo hassu nuolijuttu keskellä? Ilmeisesti se tekee koko puusta valaistumisen symbolin. No, niin valaistunut kuin voi olla, jos on kymmensorminen olento! Jos olet tarpeeksi valaistunut, tämä symboli auttaa sinua löytämään Jumalan salaisen nimen – ainakin Marko-10 sanoo niin. Mutta epäilen, että se saattaa riippua siitä, onko Jumalalla myös vain kymmenen sormea vai ei. (Jos et ole vielä tajunnut, Marko-10 ei harrasta matematiikkaa, vaan baha’i-mystiikkaa.)
Aivan, ja koska Markolla on kymmenen sormea, hän luulee, että YKSIN on maaginen luku, joka sitoo yhteen maailmankaikkeuden yhdistävän blaa-blaa-blaan ja parantaa syövän, antaa meille ilmaista energiaa ja ehkä parantaa myös kaljuuntumisen. Miksi? Koska ilmeisesti maailmankaikkeus todella välittää siitä, että hänellä on vain kymmenen sormea yhdentoista sijasta.
Kiitos tuosta selityksestä, Marko-11. Toivon sinulle hyvää matkaa takaisin Wunfishiaan (tiedän, matka täältä sinne on pitkä, ja hassuja juttuja on joka puolella!) Ai niin, ja kiitos, että esittelit minut serkullesi Blufishiasta, Marko-12:lle (olen varma, että kaikki ymmärtävät, miksi hänen nimensä on Marko-12). Marko-12 teki oman maagisen analyysinsä kahdestatoista perusluvusta. Hän keksi todella hienon pyörrekaavion, joka on kuin kotkan ja pentagrammin yhdistelmä.
Sattumaa? Ei varmasti ole. Olen varma, että se on maailmankaikkeuden tapa kertoa hänelle, että hän nousee suuriin korkeuksiin, jos hän vain kurkottaa tähtiin.
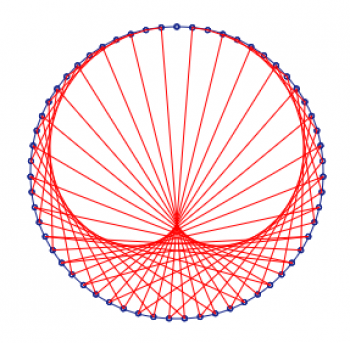
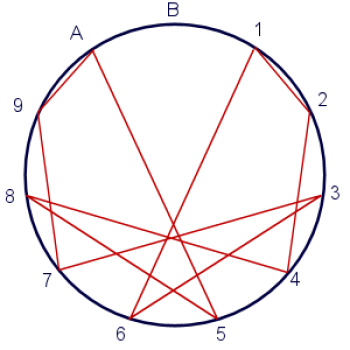
Tietenkään edes Marko-12 ei vedä vertoja muinaisten babylonialaisten nerokkuudelle; jos vain nykypäivän vortex-pohjaiset ”matemaatikot” olisivatkin yhtä kehittyneitä kuin nuo kaverit, heidän vortex-diagramminsa olisi näyttänyt tältä hämmästyttävältä taideteokselta! Ja kyllä, se on todellakin yksi ainoa silmukka, joka osuu ympyrän jokaiseen numeroon lukuun ottamatta heidän peruskuudenkymmenen numeroa 59. Kaikella kunnioituksella Marko-10:tä kohtaan, viisikymmentäyhdeksän on paljon siistimpi kuin yhdeksän!
Loppuhuomautus: VBM-ihmiset (Vortex Based Math) uskovat, että heidän maaginen kaavionsa on ”jumalallinen koodi”, mutta uskotpa tai et Galileon toteamukseen ”Matematiikka on kieli, jolla Jumala on kirjoittanut maailmankaikkeuden”, ei voi kiistää, etteikö peruskymppi olisi täysin inhimillinen konstruktio. Jos siis heidän kaavionsa on ”jumalallinen”, niin ovat myös kaikki ne lukemattomat (kirjaimellisesti äärettömät!) kauniit kaaviot (ja niihin liittyvät upeat kuviot!), jotka he jättävät huomiotta, koska ne ovat sidottuja numeroon kymmenen ja jumiutuvat siihen.
Minulta kesti yhteensä 5 minuuttia kehittää tiukka matemaattinen todiste siitä, että jos työskentelet peruslukuna N, N-1:llä on heidän ”maaginen luku” -käyttäytymisensä. Jos he olisivat oikeita matemaatikkoja, he voisivat tehdä tällaista työtä, mutta he ovat baha’i-mystikkoja matemaatikkojen sijaan, eivätkä näe metsää oman surullisen pikkujoulukuusensa takia…
Sen sijaan, että tuhlaat aikaasi heidän kanssaan, pidä mieluummin oikeasti hauskaa – opettele työskentelemään muillakin emäksillä kuin perusluvulla kymmenen, ja luo sitten omia pyörrekaavioita. Auttavatko ne sinua luomaan vapaata energiaa? Tai parantaa aknea? Ei tietenkään, mutta ne ovat varmasti kauniita, ja ne toimivat myös todella mukavina Rorchach-testeinä, jotka kertovat sinulle enemmän itsestäsi kuin maailmankaikkeuden luonteesta.
Professori Puzzler
P.S. Tässä on visuaalinen apuväline, joka auttaa sinua saamaan esimakua ”pyörrekaavioista” muissa emäksissä: Beyond Vortex Based Math