Rakenna tasasivuinen kolmio – MathBitsNotebook (Geo

Tasasivuinen kolmio MathBitsNotebook.com Topikaalinen pääpiirteittäin | Geometrian pääpiirteittäin | MathBitsin opettajaresurssit Käyttöehdot Yhteyshenkilö: Donna Roberts

Käytä konstruktiota piirtäessäsi vain kompassia ja viivainta. Ei vapaalla kädellä piirtämistä!

Tehdään KOLME tasasivuisen kolmion rakennetta. Ensimmäisessä konstruoidaan tasasivuinen kolmio, kun yhden sivun pituus on annettu, ja kahdessa muussa konstruoidaan ympyrään kirjoitettu tasasivuinen kolmio.

Annetaan: kolmion yhden sivun pituus Konstruoidaan: tasasivuinen kolmio

Vaiheet:
1. Aseta kompassin kärki pisteeseen A ja mittaa etäisyys pisteeseen B. Heilauta tämän kokoinen kaari segmentin yläpuolelle (tai alapuolelle).
2. Muuttamatta kompassin jänneväliä aseta kompassin kärki pisteeseen B ja heilauta sama kaari, joka risteää ensimmäisen kaaren kanssa.
3. Merkitse leikkauspiste tasasivuisen kolmion kolmanneksi kärkipisteeksi.

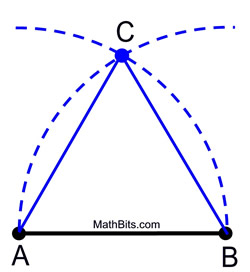Katso täysiä ympyröitä työssään.

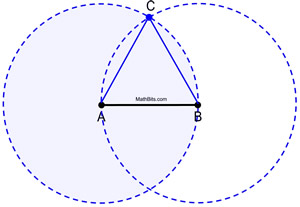Konstruktiotodistus: Ympyrä A on kongruentti ympyrän B kanssa, koska molemmat on muodostettu käyttäen samaa säteen pituutta AB. Koska AB ja AC ovat ympyrän A säteiden pituuksia, ne ovat yhtä suuret. Vastaavasti AB ja BC ovat ympyrän B säteitä, ja ne ovat yhtä suuret. Näin ollen AB = AC = BC substituution (tai transitiivisen ominaisuuden) perusteella. Koska yhtenevillä segmenteillä on samat pituudet, ja ΔABC on tasasivuinen (sillä on kolme yhtenevää sivua).

VAIHEET:
1. Aseta kompassikärki paperille ja piirrä ympyrä. (Pidä tämä kompassiväli!)
2. Aseta piste, joka on merkitty A:lla, mihin tahansa ympyrän kehälle lähtöpisteeksi.
3. Muuttamatta kompassin jänneväliä aseta kompassin piste A:n kohdalle ja heilauta pieni kaari ympyrän kehän poikki.
4. Muuttamatta kompassin jänneväliä siirrä kompassin piste edellisen kaaren ja kehän leikkauspisteeseen ja tee toinen pieni kaari ympyrän kehälle.
5. Valitse kompassin piste A:n kohdalle. Toista tätä ympyrän ympäri ”astumista”, kunnes palaat pisteeseen A.
6. Alkaen pisteestä A, yhdistä ympyrän kaikki muut kaaret tasasivuisen kolmion muodostamiseksi.

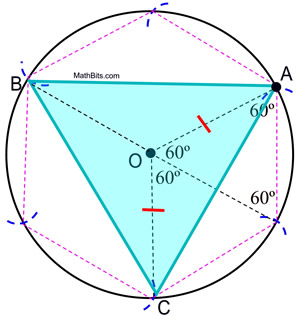Katso kirjoitetun säännöllisen kuusikulmion todistuksesta lisätietoja, jotka koskevat tämän konstruktion todistusta.

Konstruktion todistus: Kirjoitetun säännöllisen kuusikulmion todistus osoittaa, että säännöllisen kuusikulmion keskuskulmat sisältävät 60º. Tähän ympyrään kirjoitetun kolmion keskuskulmat sisältävät 120º. Koska ΔAOC on tasakylkinen (OA ja OC ovat säteiden pituudet), m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA SAS:n mukaan. CPCTC:n mukaan ∠OCB ∠OCA ja m∠OCB = 30º korvaamalla ja m∠BCA = 60º. Vastaavalla tavalla saadaan m∠ACB = m∠CBA = m∠BAC = 60º ja tasasivuinen ΔABC.

VAIHEET:
1. Aseta kompassin kärki paperille ja piirrä ympyrä, O. (Pidä tämä kompassin jänneväli!)
2. Piirrä viivoitinta käyttäen ympyrän halkaisija ja merkitse päätepisteet P ja B.
3. Muuttamatta kompassin jänneväliä aseta kompassin kärki P:n kohdalle ja piirrä täysi ympyrä.
4. Merkitse molempien ympyrän kehien leikkauspisteet A:lla ja C:llä.
5. Merkitse ympyrän kahden kehän kehän leikkauspisteet A ja C:llä. Piirrä segmentit A:sta B:hen, B:stä C:hen ja C:stä A:han muodostaaksesi tasasivuisen kolmion.

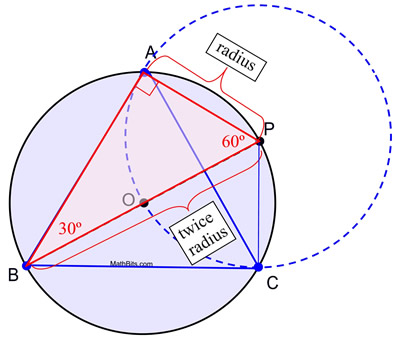
Konstruktion todistus: Tässä konstruktiossa käytetään hyväksi sitä, että puoliympyrän sisään kirjoitettu kulma on suorakulma ja että 30º-60º-90º kolmion lyhyen jalan pituus on puolet hypotenuusan pituudesta. Tässä konstruktiossa ympyrä O ja ympyrä P ovat yhteneviä, koska niiden säteen pituus on sama. AP on ympyrän P säteen pituus ja säteet AP = OP. OP on myös ympyrän O säteen pituus (yhdessä OB:n kanssa) ja halkaisija BP = BO + OP = 2 OP. Korvaamalla BP = 2 AP saadaan m∠ABP = 30º:lle tarvittavat ehdot. Näin ollen m∠APB = 60º. Vastaavalla argumentilla voidaan todeta, että ΔPBC:lle m∠PBC = 30º ja m∠BPC = 60º, jolloin ΔPBC ΔPBA ASA:lla (jaetulla sivulla B:stä P:hen).
Nyt , koska ne ovat kahden yhtenevän kolmion vastaavat sivut, mikä tekee ΔABC:stä tasakylkisen. ∠BAC ∠BCA, koska tasakylkisen kolmion peruskulmat ovat yhtenevät.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º kulmien yhteenlaskun postulaatin ja substituution avulla. m∠BAC + m∠BCA + m∠ABC = 180º, koska kolmion kulmien mittojen summa on 180º. Koska m∠BAC + m∠BAC + 60º = 180º korvaamalla tiedämme, että 2m∠BAC = 120º ja m∠BAC = 60º. Näin ollen m∠BCA on myös 60º substituution avulla, jolloin ΔABC on tasasivuinen.