Poissonin regressioanalyysi SPSS Statistics -ohjelmalla

Esittely

Poissonin regressioanalyysia käytetään ennustamaan riippuvaista muuttujaa, joka koostuu ”laskentatiedoista” ottaen huomioon yksi tai useampi riippumaton muuttuja. Muuttujaa, jota haluamme ennustaa, kutsutaan riippuvaiseksi muuttujaksi (tai joskus vaste-, tulos-, tavoite- tai kriteerimuuttujaksi). Muuttujia, joita käytämme riippuvan muuttujan arvon ennustamiseen, kutsutaan riippumattomiksi muuttujiksi (tai joskus ennustajiksi, selittäviksi tai regressiomuuttujiksi). Tässä ”keskeytysten määrä” on riippuvainen muuttuja, kun taas ”sukupuoli”, ”rotu”, ”kieli” ja ”vammaisasema” ovat kaikki nimellisiä riippumattomia muuttujia.

Esimerkki 2: Voisit käyttää Poissonin regressiota tutkiaksesi, kuinka monta kertaa australialaiset laiminlyövät luottokorttimaksunsa viiden vuoden aikana, perustuen sellaisiin ennustetekijöihin kuin ammattiasema (työllinen, työtön), vuosipalkka (Australian dollareina), ikä (vuosina), sukupuoli (mies ja nainen) ja maan työttömyysasteet (työttömien osuus). Luottokorttien takaisinmaksuhäiriöiden määrä on tässä riippuvainen muuttuja, kun taas ammattiasema ja sukupuoli ovat nimellisiä riippumattomia muuttujia ja vuosipalkka, ikä ja maan työttömyysaste ovat jatkuvia riippumattomia muuttujia.

Esimerkki #3: Voisit käyttää Poissonin regressiota tutkiaksesi, kuinka monta ihmistä on edelläsi jonossa sairaalan tapaturma-& päivystysosastolla (A&E) perustuen ennustetekijöihin, kuten saapumistapa A&E:hen (ambulanssi tai omatoiminen sisäänkirjautuminen), vamman arvioitu vaikeusaste triagessa (lievä, keskivaikea, vakava), kellonaika ja viikonpäivä. Tässä ”jonossa edellä olevien ihmisten määrä” on riippuvainen muuttuja, kun taas ”saapumistapa” on nimellinen riippumaton muuttuja, ”arvioidun vamman vaikeusaste” on järjestyslukuinen riippumaton muuttuja ja ”vuorokaudenaika” ja ”viikonpäivä” ovat jatkuvia riippumattomia muuttujia.

Esimerkki #4: Voisit käyttää Poissonin regressiota tutkiaksesi niiden opiskelijoiden lukumäärää, jotka saavat 1. luokan arvosanan MBA-ohjelmassa perustuen ennustetekijöihin, kuten heidän valitsemiensa valinnaisten kurssien tyyppeihin (pääasiassa numeeriset kurssit, pääasiassa kvalitatiiviset kurssit, sekoitus numeerisia ja kvalitatiivisia kursseja) ja heidän GPA-arvosanaansa ohjelmaan tullessaan. Tässä tapauksessa ”1. luokan opiskelijoiden määrä” on riippuvainen muuttuja, kun taas ”valinnaiset kurssit” on nimellinen riippumaton muuttuja ja ”GPA” on jatkuva riippumaton muuttuja.

Toteutettuasi Poissonin regression voit määrittää, mitkä riippumattomat muuttujat (jos sellaisia on) vaikuttavat tilastollisesti merkitsevästi riippuvaan muuttujaan. Kategoristen riippumattomien muuttujien osalta voit määrittää yhden ryhmän (esim. vuoristoradalla ajavien ”lasten” kuolemantapaukset) ja toisen ryhmän (esim. vuoristoradalla ajavien ”aikuisten” kuolemantapaukset) lukumäärän prosentuaalisen kasvun tai laskun. Jatkuvien riippumattomien muuttujien osalta pystyt tulkitsemaan, miten yhden yksikön lisäys tai vähennys kyseisessä muuttujassa liittyy riippuvaisen muuttujasi lukumäärien prosentuaaliseen lisäykseen tai vähennykseen (esim. 1 000 dollarin palkan vähennys – riippumaton muuttuja – prosentuaaliseen muutokseen siinä, kuinka monta kertaa australialaiset laiminlyövät luottokorttimaksujaan – riippuvainen muuttuja).

Tämässä ”pikakäynnistysoppaassa” opastetaan, miten Poissonin regressio suoritetaan SPSS Statistics -ohjelmalla sekä miten testin tuloksia tulkitaan ja raportoidaan. Ennen kuin esittelemme tämän menettelyn, sinun on kuitenkin ymmärrettävä erilaiset oletukset, jotka aineistosi on täytettävä, jotta Poisson-regressio antaa pätevän tuloksen. Käsittelemme näitä oletuksia seuraavaksi.

Huomautus: Tällä hetkellä meillä ei ole tämän oppaan premium-versiota verkkosivujemme tilausosassa.

SPSS Statistics

oletukset

Kun päätät analysoida tietojasi Poissonin regression avulla, osa prosessia käsittää sen tarkistamisen, että halutut tiedot voidaan todella analysoida Poissonin regression avulla. Tämä on tehtävä, koska Poisson-regression käyttö on tarkoituksenmukaista vain, jos aineistosi ”läpäisee” viisi oletusta, jotka vaaditaan, jotta Poisson-regressio antaisi pätevän tuloksen. Käytännössä näiden viiden oletuksen tarkistaminen vie suurimman osan ajastasi, kun teet Poisson-regressiota. On kuitenkin tärkeää, että teet tämän, koska ei ole harvinaista, että aineisto rikkoo (eli ei täytä) yhtä tai useampaa näistä oletuksista. Vaikka tietosi eivät täyttäisikään jotakin näistä oletuksista, on usein olemassa ratkaisu, jolla asia voidaan ratkaista. Tarkastellaan ensin näitä viittä oletusta:

• Oletus #1: Riippuva muuttujasi koostuu laskentatiedoista. Laskentatiedot eroavat muissa tunnetuissa regressiotyypeissä mitattavista tiedoista (esim. lineaarinen regressio ja moninkertainen regressio edellyttävät riippuvaisia muuttujia, jotka mitataan ”jatkuvalla” asteikolla, binominen logistinen regressio edellyttää riippuvaista muuttujaa, joka mitataan ”dikotomisella” asteikolla, ordinaalinen regressio edellyttää riippuvaista muuttujaa, joka mitataan ”ordinaalisella” asteikolla, ja moninomaalinen logistinen regressio edellyttää riippuvaista muuttujaa, joka mitataan ”nominaalisella” asteikolla). Sen sijaan laskentamuuttujat edellyttävät kokonaislukumuuttujia, joiden on oltava nolla tai suurempi. Yksinkertaistettuna ”kokonaisluku” on ”kokonainen” luku (esim. 0, 1, 5, 8, 354, 888, 23400 jne.). Koska laskentatietojen on myös oltava ”positiivisia” (eli koostuttava ”ei-negatiivisista” kokonaislukuarvoista), ne eivät voi koostua ”miinusarvoista” (esim. sellaisia arvoja kuin -1, -5, -8, -354, -888 ja -23400 ei pidettäisi laskentatietoina). Lisäksi joskus ehdotetaan, että Poissonin regressio suoritetaan vain silloin, kun laskentakeskiarvo on pieni arvo (esim. alle 10). Jos laskentatietoja on paljon, toisenlainen regressio saattaa olla sopivampi (esim. moninkertainen regressio, gammaregressio jne.).
  Esimerkkejä laskentamuuttujista ovat yli kolme tuntia myöhästyneiden lentojen määrä Euroopan lentokentillä, Washingtonin koulujen erottamien oppilaiden määrä Yhdysvalloissa, montako kertaa australialaiset laiminlyövät luottokorttimaksunsa viiden vuoden aikana, kuinka monta ihmistä on edelläsi jonossa sairaalan ensiapupoliklinikalla, kuinka monta opiskelijaa saa MBA-ohjelmassa arvosanan 1 (yleensä alle 5) ja kuinka monta ihmistä kuolee vuoristorataonnettomuuksissa Yhdysvalloissa.
• Oletus #2: Sinulla on yksi tai useampi riippumaton muuttuja, joita voidaan mitata jatkuvalla, ordinaalisella tai nominaalisella/dichotomisella asteikolla. Ordinaaliset ja nominaaliset/dikotomiset muuttujat voidaan laajasti luokitella kategorisiksi muuttujiksi.
  Esimerkkejä jatkuvista muuttujista ovat tarkistusaika (mitattuna tunteina), älykkyysosamäärä (mitattuna älykkyysosamääräpistemäärällä), tenttisuoritukset (mitattuna 0-100) ja paino (mitattuna kiloina). Esimerkkejä ordinaalisista muuttujista ovat Likert-kysymykset (esim. 7-pisteinen asteikko ”täysin samaa mieltä” – ”täysin eri mieltä”) ja muut tavat asettaa luokkia paremmuusjärjestykseen (esim. 3-pisteinen asteikko, jolla selitetään, kuinka paljon asiakas piti tuotteesta, ja joka vaihtelee asteikosta ”Ei kovin paljon” asteikkoon ”Kyllä, paljon”). Esimerkkejä nimellisistä muuttujista ovat sukupuoli (esim. kaksi ryhmää – mies ja nainen – eli dikotominen muuttuja), etninen alkuperä (esim. kolme ryhmää: valkoihoinen, afroamerikkalainen ja latinalaisamerikkalainen) ja ammatti (esim. viisi ryhmää: kirurgi, lääkäri, sairaanhoitaja, hammaslääkäri, terapeutti). Muista, että ordinaaliset ja nominaaliset/dikotomiset muuttujat voidaan laajasti luokitella kategorisiksi muuttujiksi. Voit lukea lisää muuttujista artikkelistamme: Muuttujatyypit.
• Oletus #3: Havaintojen tulisi olla riippumattomia. Tämä tarkoittaa, että jokainen havainto on riippumaton muista havainnoista; eli yksi havainto ei voi antaa tietoa toisesta havainnosta. Tämä on erittäin tärkeä oletus. Riippumattomien havaintojen puuttuminen on useimmiten tutkimuksen suunnitteluun liittyvä ongelma. Yksi tapa testata havaintojen riippumattomuuden mahdollisuutta on verrata malliin perustuvia standardivirheitä robusteihin virheisiin sen selvittämiseksi, onko niissä suuria eroja.
• Oletus #4: Lukumäärien jakauma (mallin ehdolla) noudattaa Poisson-jakaumaa. Yksi seuraus tästä on, että havaittujen ja odotettujen lukumäärien pitäisi olla yhtä suuria (todellisuudessa vain hyvin samanlaisia). Pohjimmiltaan tämä tarkoittaa, että malli ennustaa hyvin havaittuja lukumääriä. Tätä voidaan testata monella tavalla, mutta yksi tapa on laskea odotetut lukumäärät ja piirtää ne havaittujen lukumäärien kanssa nähdäkseen, ovatko ne samankaltaisia.
• Oletus #5: Mallin keskiarvo ja varianssi ovat samat. Tämä on seurausta oletuksesta #4; että on olemassa Poisson-jakauma. Poisson-jakaumassa varianssilla on sama arvo kuin keskiarvolla. Jos tämä oletus täyttyy, kyseessä on tasajakautuma. Usein näin ei kuitenkaan ole, vaan aineisto on joko ali- tai ylihajonnut, ja ylihajonta on yleisempi ongelma. Ylidispersion arviointiin voidaan käyttää erilaisia menetelmiä. Yksi menetelmä on Pearsonin hajontatilaston arviointi.

Voit tarkistaa oletukset #3, #4 ja #5 SPSS Statistics -ohjelmalla. Oletukset #1 ja #2 tulisi tarkistaa ensin, ennen kuin siirrytään oletuksiin #3, #4 ja #5. Muista vain, että jos et suorita näiden oletusten tilastollisia testejä oikein, Poisson-regressiota suorittaessasi saamasi tulokset eivät välttämättä ole päteviä.

Jos aineistosi rikkoo oletusta #5, mikä on erittäin yleistä Poisson-regressiota suoritettaessa, sinun on ensin tarkistettava, onko sinulla ”näennäinen Poissonin ylidispersio”. Näennäinen Poissonin ylidispersio tarkoittaa sitä, että et ole määritellyt mallia oikein siten, että aineisto näyttää ylidispersiolta. Jos Poisson-mallisi siis aluksi rikkoo oletusta tasajakautuneesta hajonnasta, sinun on ensin tehtävä Poisson-malliisi useita muutoksia tarkistaaksesi, että se on todella ylidispersiivinen. Tämä edellyttää, että teet kuusi tarkistusta mallillesi/tiedoillesi: (a) Sisältääkö Poisson-mallisi kaikki tärkeät ennustajat?; b) Sisältääkö aineistosi poikkeavia tekijöitä?; c) Sisältääkö Poisson-regressiosi kaikki asiaankuuluvat vuorovaikutustermit?; d) Pitääkö jokin ennustajistasi muuntaa?; e) Vaatiiko Poisson-mallisi lisää aineistoa ja/tai ovatko aineistosi liian harvat?; ja (f) Onko sinulla puuttuvia arvoja, jotka eivät ole satunnaisesti puuttuvia (MAR)?

Luvussa Proseduuri havainnollistamme SPSS Statistics -ohjelman menettelyä Poisson-regression suorittamiseksi olettaen, että mitään oletuksia ei ole rikottu. Ensin esittelemme esimerkin, jota käytetään tässä oppaassa.

SPSS Statistics

Esimerkki & Asetukset SPSS Statisticsissa

Pienen yliopiston tutkimusjohtaja haluaa arvioida, vaikuttaako akateemikon kokemus ja aika, joka hänellä on käytettävissään tutkimustyöhön, hänen tuottamiensa julkaisujen määrään. Siksi tutkimukseen pyydetään satunnaisotanta 21:stä yliopiston akateemisesta tutkijasta: Kymmenen on kokeneita akateemisia tutkijoita ja yksitoista uusia tutkijoita. Heidän tutkimukseen käyttämiensä tuntien määrä viimeisten 12 kuukauden aikana ja heidän tuottamiensa vertaisarvioitujen julkaisujen määrä kirjataan.

Tämän tutkimusasetelman luomiseksi SPSS Statistics -ohjelmassa luotiin kolme muuttujaa: (1) no_of_publications, joka on niiden julkaisujen lukumäärä, jotka akateemikko on julkaissut vertaisarvioiduissa lehdissä viimeisten 12 kuukauden aikana; (2) experience_of_academic, joka kuvastaa sitä, onko akateemikko kokenut (eli työskennellyt akateemisessa maailmassa vähintään 10 vuotta ja luokitellaan näin ollen ”kokeneeksi akateemikoksi”) vai onko hänestä tullut hiljattain akateemikko (ts, on työskennellyt akateemisessa työssä alle kolme vuotta, mutta vähintään vuoden, ja hänet luokitellaan näin ollen ”tuoreeksi akateemikoksi”); ja (3) no_of_weekly_hours, joka ilmaisee niiden tuntien määrän, jotka akateemisella on viikoittain käytettävissään tutkimustyöhön.

SPSS Statistics

Testausmenettely SPSS Statistics -ohjelmassa

Alla olevat 13 vaihetta osoittavat, miten analysoit aineistosi käyttämällä Poissonin regressiota SPSS Statistics -ohjelmassa silloin, kun mitään edellisessä kohdassa Oletukset esitetyistä viidestä oletuksesta ei ole rikottu. Näiden 13 vaiheen lopussa näytämme, miten voit tulkita Poisson-regression tuloksia.

1. Click Analyze > Generalized Linear Models > Generalized Linear Models… päävalikosta alla esitetyllä tavalla:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

   Sinulle avautuu alla oleva Generalized Linear Models (yleistetyt lineaariset mallit) -valintaikkuna:

   

   Published with written permission from SPSS Statistics, IBM Corporation.

2. Valitse -alueelta Poisson-loglineaarinen malli alla esitetyllä tavalla:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

   Huomaa: Vaikka Poisson-regression suorittamiseksi on tavallista valita -alueelta Poisson loglinear, voit myös suorittaa mukautetun Poisson-regression valitsemalla -alueelta Custom (Mukautettu) ja määrittelemällä sen jälkeen haluamasi Poisson-mallin tyypin Distribution: (Jakauma:), Link function: (Linkkifunktio:) ja -Parameter- (Parametri-) -vaihtoehtojen avulla.

3. Valitse -välilehdelle. Näyttöön tulee seuraava valintaikkuna:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

4. Siirrä riippuvainen muuttujasi no_of_publications 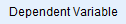-alueen Dependent variable: -ruutuun -painikkeella alla olevan kuvan mukaisesti:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

5. Valitse välilehti . Näyttöön tulee seuraava valintaikkuna:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

6. Siirrä kategorinen riippumaton muuttuja experience_of_academic Factors: -laatikkoon ja jatkuva riippumaton muuttuja no_of_weekly_hours: -laatikkoon Covariates: -laatikkoon -painikkeilla alla esitetyllä tavalla:
   

   Julkaistu SPSS Statistics, IBM Corporationin kirjallisella luvalla.

   Huomautus 1: Jos sinulla on ordinaalisia riippumattomia muuttujia, sinun on päätettävä, käsitelläänkö niitä kategorisina ja kirjataanko ne Factors: -laatikkoon vai käsitelläänkö niitä jatkuvina ja kirjataanko ne Covariates: -laatikkoon. Niitä ei voi syöttää Poisson-regressioon ordinaalimuuttujina.

   Huomautus 2: Vaikka on tyypillistä syöttää jatkuvat riippumattomat muuttujat laatikkoon Covariates:, on mahdollista syöttää sen sijaan ordinaalisia riippumattomia muuttujia. Jos kuitenkin valitset tämän, ordinaalista riippumatonta muuttujaa käsitellään jatkuvana.

   Huomautus 3: Jos napsautat -painiketta, seuraava valintaikkuna tulee näkyviin:
   
   Kohdassa -Category Order for Factors- voit valita vaihtoehdoista Ascending (nouseva), Descending (laskeva) ja Use data order (käytä tietojen järjestystä). Nämä ovat hyödyllisiä, koska SPSS Statistics muuttaa kategoriset muuttujat automaattisesti dummy-muuttujiksi. Ellet tunne dummy-muuttujia, tämä voi tehdä Poisson-regression tuloksen tulkitsemisesta hieman hankalaa kategoristen muuttujiesi kunkin ryhmän osalta. Siksi muutosten tekeminen -Category Order for Factors- alueen asetuksiin voi helpottaa tulosteen tulkintaa.

7. Valitse -välilehti. Näet seuraavan valintaikkunan:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

8. Pidä -Build Term(s)-alueella oletusarvo ja siirrä kategoriset ja jatkuvat riippumattomat muuttujat, experience_of_academic (kokemus_opiskelusta) ja no_of_weekly_hours (ei_viikoittaisia_tunteja), Factors and Covariates (tekijät ja oheismuuttujat): -ruudusta Model (malli): -ruudukkoon -painiketta käyttäen alla olevan mallin mukaisesti:
   

   Kustantuu kirjallisella luvalla SPSS Statisticsilta, IBM Corporationilta.

   Huomautus 1: Poisson-malli rakennetaan -valintaikkunassa. Määrität erityisesti, mitä päävaikutuksia sinulla on (-vaihtoehto), sekä sen, odotatko, että riippumattomien muuttujiesi välillä on vuorovaikutuksia (-vaihtoehto). Jos epäilet, että riippumattomien muuttujiesi välillä on vuorovaikutuksia, niiden sisällyttäminen malliisi on tärkeää paitsi mallisi ennusteen parantamiseksi myös ylidispersion ongelmien välttämiseksi, kuten aiemmin kohdassa Oletukset korostettiin.
   Vaikka annamme esimerkin hyvin yksinkertaisesta mallista, jossa on vain yksi päävaikutus (kategoristen ja jatkuvien riippumattomien muuttujien kokemus_opiskelusta ja ei_viikkotunteja välillä), voit helposti syöttää monimutkaisempia malleja käyttämällä , , . ja -vaihtoehtoja -Build Term(s)-alueella sen mukaan, millaisia päävaikutuksia ja vuorovaikutuksia mallissasi on.

   Huomautus 2: Voit myös rakentaa malliisi sisäkkäisiä termejä lisäämällä ne -Build Nested Term- alueen Term: -ruutuun. Meillä ei ole tässä mallissa sisäkkäisiä vaikutuksia, mutta on monia skenaarioita, joissa mallissasi voi olla sisäkkäisiä termejä.

9. Valitse -välilehti. Näet seuraavan valintaikkunan:
   

   Published with written permission from SPSS Statistics, IBM Corporation.

10. Pitäkää oletusasetukset valittuna.

    Huomaa: -Parametrien estimointi -alueella on useita eri vaihtoehtoja, jotka voit valita, mukaan lukien mahdollisuus valita eri: (a) asteikkoparametrien menetelmä (eli tai sijasta Scale Parameter Method: -kentässä), jota voidaan harkita ylidispersion ongelmien käsittelemiseksi; ja (b) kovarianssimatriisi (eli Robust estimaattori sijasta Model-based estimaattori -alueella -Covariance Matrix-), joka esittää toisen mahdollisen vaihtoehdon (muun muassa) ylidispersion ongelmien käsittelemiseksi.
    On myös useita määrityksiä, joita voit tehdä -Iterations- -alueella käsitellessäsi Poisson-mallisi epäkonvergenssikysymyksiä.

11. Valitse -välilehti. Näet seuraavan valintaikkunan:
    

    Published with written permission from SPSS Statistics, IBM Corporation.

12. Valitse Include exponential parameter estimates (Sisällytä eksponentiaaliset parametriestimaatit) -alueella, kuten alla näkyy:
    

    Published with written permission from SPSS Statistics, IBM Corporation.

    Huomautus 1: -alueella voit valita Wald- ja Likelihood-suhteen välillä sellaisten tekijöiden perusteella kuin otoskoko ja vaikutukset, joita tällä voi olla tilastollisen merkitsevyystestauksen tarkkuuteen.
    Alueella myös Lagrangen kertoimen testi voi olla hyödyllinen sen määrittämiseksi, soveltuuko Poisson-malli aineistoosi (tätä ei tosin voi suorittaa Poisson-regressiomenetelmällä).

    Huomautus 2: Voit myös valita monenlaisia muita vaihtoehtoja välilehdiltä ja . Näihin sisältyy vaihtoehtoja, jotka ovat tärkeitä tutkittaessa kategoristen muuttujiesi ryhmien välisiä eroja sekä testattaessa Poisson-regression oletuksia, kuten aiemmin kohdassa Oletukset käsiteltiin.

13. Klikkaa -painiketta. Tämä luo tulosteen.

SPSS Statistics

Poisson-regressioanalyysin tulosteen tulkinta ja raportointi

SPSS Statistics luo Poisson-regressioanalyysin tulosteeksi melko monta taulukkoa. Tässä osassa näytämme kahdeksan tärkeintä taulukkoa, joita tarvitaan Poisson-regressiomenetelmän tulosten ymmärtämiseen olettaen, että mitään oletuksia ei ole rikottu.

Mallin ja muuttujien tiedot

Tulosteen ensimmäinen taulukko on Mallin tiedot -taulukko (kuten alla näkyy). Tämä vahvistaa, että riippuvainen muuttuja on ”Julkaisujen lukumäärä”, todennäköisyysjakauma on ”Poisson” ja yhteysfunktio on luonnollinen logaritmi (eli ”Log”). Jos suoritat Poisson-regression omilla tiedoillasi, riippuvan muuttujan nimi on eri, mutta todennäköisyysjakauma ja linkkifunktio ovat samat.

Toisesta taulukosta, Case Processing Summary (Tapausten käsittelyyhteenveto), näet, kuinka monta tapausta (esim, koehenkilöt) otettiin mukaan analyysiisi (rivi ”Sisällytetty”) ja kuinka monta jätettiin pois (rivi ”Poissuljettu”), sekä molempien prosenttiosuus. Voit ajatella, että ”Excluded”-rivi osoittaa tapaukset (esim. koehenkilöt), joilla oli yksi tai useampi puuttuva arvo. Kuten alla näkyy, tässä analyysissä oli 21 koehenkilöä, eikä yhtään koehenkilöä jätetty pois (eli ei puuttuvia arvoja).

The Categorical Variable Information -taulukossa tuodaan esiin tapausten (esim. koehenkilöiden) lukumäärä ja prosentuaalinen osuus kussakin analyysissäsi olevan jokaisen riippumattoman kategorisen muuttujan kussakin ryhmässä. Tässä analyysissä on vain yksi kategorinen riippumaton muuttuja (tunnetaan myös nimellä ”tekijä”), joka oli experience_of_academic. Näet, että ryhmien lukumäärät ovat melko tasapainossa kahden ryhmän välillä (esim. 10 vs. 11). Erittäin epätasapainoiset ryhmäkoot voivat aiheuttaa ongelmia mallin sovittamisessa, mutta näemme, että tässä ei ole ongelmaa.

Jatkuvan muuttujan tiedot (Continuous Variable Information) -taulukon avulla voidaan alkeellisesti tarkastaa aineisto mahdollisten ongelmien varalta, mutta se ei ole yhtä käyttökelpoinen kuin muut kuvailevat tilastotiedot, jotka voit suorittaa erikseen ennen Poisson-regression suorittamista. Parasta, mitä voit saada tästä taulukosta, on saada käsitys siitä, onko analyysissäsi mahdollisesti ylidispersiota (eli Poisson-regression oletus #5). Voit tehdä tämän tarkastelemalla riippuvan muuttujan varianssin (sarakkeen ”Std. Deviation” neliö) ja keskiarvon (sarake ”Mean”) suhdetta. Näet nämä luvut alla:

Keskiarvo on 2,29 ja varianssi on 2,81 (1,677582), eli suhde on 2,81 ÷ 2,29 = 1,23. Poisson-jakauma olettaa, että suhde on 1 (eli keskiarvo ja varianssi ovat yhtä suuret). Näin ollen voimme nähdä, että ennen selittävien muuttujien lisäämistä on olemassa pieni määrä ylidispersiota. Meidän on kuitenkin tarkistettava tämä oletus, kun kaikki riippumattomat muuttujat on lisätty Poisson-regressioon. Tätä käsitellään seuraavassa kappaleessa.

Mallin sopivuuden määrittäminen

Soveltuvuuden hyvyys -taulukossa on monia mittareita, joiden avulla voidaan arvioida, kuinka hyvin malli sopii. Keskitymme kuitenkin Pearsonin khiin neliö -rivin ”Value/df”-sarakkeen arvoon, joka tässä esimerkissä on 1,108, kuten alla näkyy:

Arvo 1 viittaa tasajakauteen, kun taas arvot, jotka ovat suurempia kuin 1, viittaavat ylihajontaan ja arvot, jotka ovat pienempiä kuin 1, viittaavat alihajontaan. Yleisin tasajakautumisoletuksen rikkomustyyppi on ylidispersio. Kun otoskoko on tässä esimerkissä niin pieni, arvo 1,108 ei todennäköisesti ole vakava rikkomus tätä olettamusta vastaan.

Omnibus Test -taulukko sopii jonnekin tämän ja seuraavan jakson väliin. Se on todennäköisyyssuhdetesti siitä, parantavatko kaikki riippumattomat muuttujat yhdessä mallia verrattuna pelkkään intercept-malliin (eli malliin, johon ei ole lisätty riippumattomia muuttujia). Kun kaikki riippumattomat muuttujat ovat mukana esimerkkimallissamme, saamme p-arvoksi 0,006 (eli p = 0,006), mikä viittaa tilastollisesti merkitsevään kokonaismalliin, kuten alla olevasta ”Sig.”-sarakkeesta käy ilmi:

Nyt kun tiedetään, että kaikkien riippumattomien muuttujien lisääminen synnyttää tilastollisesti merkitsevän mallin, halutaan tietää, mitkä nimenomaiset riippumattomat muuttujat ovat tilastollisesti merkitseviä. Tätä käsitellään seuraavassa kappaleessa.

Mallin vaikutukset ja riippumattomien muuttujien tilastollinen merkitsevyys

Testit mallin vaikutuksista -taulukossa (kuten alla on esitetty) näkyy kunkin riippumattoman muuttujan tilastollinen merkitsevyys sarakkeessa ”Sig.”:

Mallin leikkauspisteestä (intereptistä) ei tavallisesti ole mitään hyötyä. Näemme kuitenkin, että akateemikon kokemus ei ollut tilastollisesti merkitsevä (p = .644), mutta viikoittaisten työtuntien määrä oli tilastollisesti merkitsevä (p = .030). Tämä taulukko on hyödyllinen lähinnä kategoristen riippumattomien muuttujien kohdalla, koska se on ainoa taulukko, jossa otetaan huomioon kategorisen muuttujan kokonaisvaikutus, toisin kuin alla olevassa Parameter Estimates -taulukossa:

Tässä taulukossa esitetään sekä Poisson-regression kerroinestimaatit (sarake ”B”) että kertoimien eksponenttiarvot (sarake ”Exp(B)”). Jälkimmäiset ovat yleensä informatiivisempia. Näitä eksponentoituja arvoja voidaan tulkita useammalla kuin yhdellä tavalla, ja näytämme tässä oppaassa yhden tavan. Tarkastellaan esimerkiksi viikoittain tehtyjen työtuntien määrää (eli riviä ”no_of_weekly_hours”). Eksponenttiarvo on 1,044. Tämä tarkoittaa, että julkaisujen määrä (eli riippuvan muuttujan luku) on 1,044 kertaa suurempi jokaista viikossa tehtyä lisätuntia kohden. Toinen tapa sanoa tämä on, että julkaisujen määrä kasvaa 4,4 prosenttia jokaista viikossa tehtyä lisätuntia kohden. Samanlainen tulkinta voidaan tehdä kategoriselle muuttujalle.

Kokoonpano

Viikoittain tehtyjen työtuntien määrää koskevat tulokset voisi kirjoittaa seuraavasti: