Pistesymmetria on olemassa, kun kuvio piirretään yhden pisteen ympärille.

Tätä pistettä kutsutaan kuvion keskipisteeksi tai symmetrian keskipisteeksi. Viereisessä kuvassa havaitaan, että kuvion pistettä X vastaavaa pistettä X’ vastaa keskipisteen toisella puolella oleva piste X’, joka on suoraan X:n vastakohta ja joka sijaitsee kuvion päällä. Sanomme, että kuvio on symmetrinen keskipisteen suhteen.
Huomautus:
Kun käännämme kuviota 180° ja se saa takaisin alkuperäisen muotonsa, sanomme, että kuvio on pistesymmetrinen.
Esimerkkejä kuviosta, jossa on pistesymmetria:
● Kaikki englannin aakkosten kirjaimet.
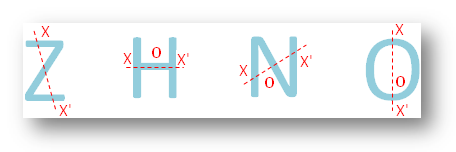
● Erilaisia geometrisia kuvioita.
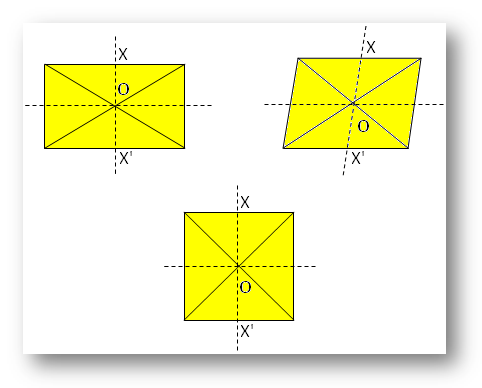
Huomautus:
Tässä O onsymmetriakeskipiste.
Suhteessa X:ään on olemassa X’, niin että X’ on X:n vastakohtana suoraan X:n toisella puolella O:ta.
Mitkä ovat ne ehdot, jotka muoto tai kuvio täyttääpistesymmetriaa varten?
Edellytykset, jotkamuoto tai kuvio täyttääpistesymmetriaa varten eli jokaisella osalla tulee olla vastaava osa
– etäisyyden tulee olla yhtä suuri keskipisteestä
– mutta vastakkaiseen suuntaan.
● Aiheeseen liittyviä käsitteitä
● Lineaarinen symmetria
● Symmetriaviivat
● Pyörimissymmetria
● Pyörimissymmetrian järjestys
● Pyörimissymmetriatyypit
● Heijastuminen
● Pisteen heijastuminen x-akselilla
● Pisteen heijastuminen y-akselilla
● Pisteen heijastus y-akselilla
● Pisteen heijastus origossa
● Kierto
● 90 asteen kierto myötäpäivään
● 90 asteen kierto vastapäivään
● 180 asteen kierto
7. luokan matematiikan tehtävät
8. luokan matematiikan harjoitukset
Pisteen symmetriasta KOTISIVULLE