Ennen kuin aloitamme, meidän on tehtävä joitakin oletuksia.
Ensiksi, työskentelemme newtonilaisten nesteiden kanssa. Tämä on yksinkertaisin matemaattinen tapa ottaa huomioon nesteen viskositeetti. Ei ole olemassa todellisia nesteitä, jotka kuuluisivat täydellisesti tähän kategoriaan, mutta useimmissa tapauksissa ilmaa ja vettä voidaan käsitellä newtonilaisena nesteenä. Toinen hyvin tärkeä hypoteesimme on, että neste on kokoonpuristumaton. Tämä tarkoittaa, että sen tiheys, rho, on vakio.
Massan säilyminen

Ensimmäinen yhtälö kertoo, että käsittelemämme nesteen massa säilyy. Neste voi muuttaa muotoaan, mutta tämä yhtälö kertoo, että massa pysyy samana alusta loppuun.
Puhutaan nyt matematiikasta. Kirjain u edustaa nesteen nopeutta, ja se on vektori. Sillä on kolme komponenttia, voimme kutsua niitä u, v, w, ja ne edustavat nesteen nopeutta x-, y- ja z-suunnassa. Kreikkalainen kirjain nabla ∇, jota seuraa piste, on divergenssioperaattori. Tämä tarkoittaa, että meidän on differentioitava sen komponentit joka suuntaan (tässä tapauksessa x, y, z).

Ensimmäinen derivaatta kertoo, miten nopeuden x-komponentti muuttuu, kun liikumme x-suunnassa. Sama pätee kahteen muuhun derivaataan. Koska tämä yhtälö on yhtä suuri kuin nolla, se osoittaa meille, että massa säilyy.
Momentin säilyminen

Kakkosyhtälö on itse asiassa kolmen differentiaaliyhtälön joukko. Tämä on se, jota voidaan kuvata Newtonin toiseksi laiksi nesteille. Jos laajennamme lausekkeen, saamme monimutkaisen systeemin.
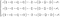
Koska se on paljon yksinkertaisempi ymmärtää, aiomme keskittyä impulssin säilymiseen ei laajennettuna.
Kun työskentelemme nesteiden kanssa, voimme sanoa, että massa ja tiheys ovat samat asiat (kunhan niiden tilavuus on sama). Jos tarkastelemme kahta nestettä, voimme sanoa, että tiheämpi on ”raskaampi” (esim. elohopea ja vesi). Tällöin kreikkalainen kirjain ρ (rho) on nesteen tiheys.
Meillä on massa, nyt palataksemme Newtonin toiseen lakiin tarvitsemme kiihtyvyyden. Se on juuri nopeusvektorin aikaderivaatan tulos.

Nyt jäljelle jäävät vain yhtäsuuruusmerkin oikealla puolella olevat termit, ja ne edustavat kaikkia nesteeseen kohdistuvia voimia.
Ensimmäinen termi ∇p on paineen gradientti. Se edustaa paine-eroa tilassa, jossa neste on. Jos on esimerkiksi vyöhyke, jossa on matalapaine ja toinen, jossa on korkeampi paine, neste siirtyy korkeapaineisesta osasta matalapaineisempaan. Gradientti p kertoo kaiken tämän.
Toinen termi kuvaa nesteen viskositeettia. Ajattele kahta erilaista nestettä, kuten vettä ja hunajaa. Kun kaadat lasillisen vettä, se putoaa nopeasti ja helposti. Kun teet saman hunajan kanssa, se on tahmeaa ja kaatuu hyvin hitaasti. Tätä tuo lauseke kertoo.
Viimeinen termi, F, on helpoin, koska se edustaa kaikkia ulkoisia voimia, jotka voivat kohdistua kyseiseen nesteeseen. Yleensä voima, jota tässä tarkastelemme, on painovoima.
Tässä se on, kaikki nuo hienot symbolit ja kirjaimet tarkoittavat vain voimaa = massa x kiihtyvyys.
Navier-Stokesin yhtälöiden käyttö
Koska näiden yhtälöiden ratkominen on niin monimutkaista, niiden käyttämiseksi joudumme tekemään paljon likiarvoja. Esimerkkejä ovat Poiseuille- ja Couette-virtaus. Nämä kaksi tiedemiestä pystyivät monien oletusten avulla löytämään ratkaisun Navier-Stokesin yhtälöille hyvin erityistä sovellusta varten. Jos haluamme kuitenkin käyttää niitä monimutkaisempaan tehtävään, kuten sääennusteisiin, meidän on tehtävä jotakin muuta.
Yleisin tapa käyttää näitä yhtälöitä on muuntaa ne Reynoldsin keskiarvon avulla. Tämä on kehittynyt matemaattinen prosessi ja tuloksena ovat Reynoldsin yhtälöt. Niitä kutsutaan yleensä RANS-yhtälöiksi (mikä tarkoittaa Reynoldsin keskiarvoistamia Navier-Stokesin yhtälöitä).
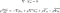
Näitä yhtälöitä käytetään silloin, kun fluidi virtaa turbulenttisesti. Ne näyttävät lähes täsmälleen samalta kuin Navier-Stokesin yhtälöt, lukuun ottamatta viimeistä termiä. Tätä kutsutaan Reynoldsin jännitystensoriksi. Se on suure, jonka avulla voimme ottaa huomioon nesteen turbulenssin.
RANS-yhtälöissä käyttämämme suureet keskiarvoistetaan aikavälein. Tämän aikavälin on oltava riittävän pieni, jotta tutkimamme ilmiö voidaan havaita. Samalla sen on oltava riittävän suuri, jotta turbulenssin vaikutus menettää merkityksensä.
Oikein oletuksin nämä yhtälöt toimivat. Tiedämme, miten niitä voidaan käyttää F1-autojen nopeuttamiseen, avaruusaluksen saamiseen ISS:lle ja sääennusteiden laatimiseen. Saatat siis ihmetellä, miksi näiden yhtälöiden todistaminen on miljoonan dollarin arvoista?
Miljoonan dollarin palkinto
Fysiikan näkökulmasta nämä yhtälöt ovat vain Newtonin toinen laki, joka toimii nesteiden kanssa. Kun teemme joitakin oletuksia ja yksinkertaistuksia, voimme tehdä niillä hämmästyttäviä asioita.
Todellinen ongelma on tämä. Näiden yhtälöiden ratkaiseminen ilman approksimaatioita on vain hirveän monimutkaista. Se on niin vaikeaa, että ei ole todistettu, että ratkaisut todella ovat olemassa. Ja tässä kohtaa Millennium-palkinto astuu kuvaan.
Ongelman virallinen lausunto (löytyy täältä) on:
Todistakaa tai antakaa vastaesimerkki seuraavasta väitteestä: Kolmessa avaruusulottuvuudessa ja ajassa, kun on annettu alkunopeuskenttä, on olemassa vektorinopeuskenttä ja skalaaripainekenttä, jotka ovat molemmat sileitä ja globaalisti määriteltyjä, ja jotka ratkaisevat Navier-Stokesin yhtälöt.
Tämä tarkoittaa, että voittaaksesi palkinnon sinun on tehtävä kolme asiaa:
- Varmista, että ratkaisu on olemassa
- Ratkaisun on oltava olemassa jokaisessa avaruuden pisteessä
- Ratkaisun on oltava sileä. Tämä tarkoittaa, että pieni muutos alkuolosuhteissa tuottaa vain vähän vaihtelua tulokseen.
Insinöörille riittää yleensä tieto siitä, että nämä yhtälöt toimivat, vaikka vain jollakin approksimaatiotasolla. Matemaatikolle on kuitenkin hyvin tärkeää tietää, ovatko ratkaisut olemassa ja miten ne käyttäytyvät.
Saatat nyt ajatella, että jos ne toimivat sellaisenaan, ajan ja energian käyttäminen todistuksen etsimiseen on täyttä ajanhukkaa. No, kuten monet teknologiset edistysaskeleet ihmiskunnan historiassa, tulos ei ehkä tunnu kovin tärkeältä. Tärkeää on polku sinne pääsemiseksi, joka voi tuoda uutta tietoa ja parannuksia elämäämme.
Ajatellaanpa avaruuslentoja. Jos ihmiset eivät olisi koskaan päättäneet lähteä kävelemään kuuhun, meillä ei olisi monia esineitä, joita käytetään parantamaan elämäämme. Magneettikuvauslaitteet ja sydämentahdistimet ovat peräisin avaruustutkimusta varten kehitetyistä teknologioista. Nykyään lääkärit ympäri maailmaa käyttävät niitä päivittäin pelastaakseen ihmishenkiä. Sama pätee myös täällä. Tie Navier-Stokesin yhtälöiden ratkaisun löytämiseen auttaa meitä parantamaan ymmärrystämme nesteistä ja muusta. Se voi johdattaa meidät uusiin löytöihin ja edellyttää todennäköisesti uuden matematiikan keksimistä. Tätä voidaan sitten käyttää moniin muihin ongelmiin vastaamiseen ja uusien teknologioiden keksimiseen, jotta voimme parantaa elämäämme ja tehdä meistä parempia.