Mikä on solukalvon läpäisevyys?
Lukutila
Yksi kaikkien elävien organismien tunnusomaisista ominaisuuksista on se, että ne sisältävät omaleimaista ionien ja pienten molekyylien sekoitusta. Koostumus ei ainoastaan poikkea ympäristöstä, vaan se voi vaihdella myös solun sisällä. Esimerkiksi vetyionien pitoisuus joissakin solukompartimenteissa voi olla 104 kertaa suurempi kuin toisissa (mitokondriot saavuttavat pH:n, joka on jopa 8; lysosomit, joiden pH on jopa 4, BNID 107521, 106074). Solunulkoisten ja solunsisäisten nestekompartimenttien Ca2+ -ionien pitoisuuksien suhde voi jälleen olla 104-kertainen (BNID 104083). Tämä konsentraatioero on niin suuri, että Ca2+ -ionin kuljettaminen kalvon läpi solunsisäisestä osastosta solunulkoiseen osastoon vaatii useamman kuin yhden protonin tai natriumionin energiaa, joka virtaa protonimoottorivoimagradienttia pitkin. Tämän havaitsemiseksi lukijan on syytä muistaa nyrkkisääntö, joka on esitetty tricks of the trade -luettelossamme ja jonka mukaan suuruusluokan potentiaalieron aikaansaaminen vaatii 6 kJ/mol (≈2 kBT). Tämä energia voidaan saavuttaa esimerkiksi kuljettamalla yksi sähkövaraus 60 mV:n potentiaalieron läpi. Neljän kertaluokan pitoisuussuhteen saavuttaminen edellyttäisi tällöin varauksen kuljettamista alaspäin noin 240 mV:n elektronin liikkeellepanevalla voimalla (itse asiassa vielä enemmän kalsiumionin kaksoisvarauksen vuoksi). Tämä on hyvin lähellä kalvon läpilyöntijännitettä, jota käsiteltiin vinjetissä ”Mikä on sähköinen potentiaaliero kalvojen yli?”. Ca2+:n suuri pitoisuussuhde saavutetaankin yleensä kytkemällä se kolmen natriumionin kuljetukseen tai ATP:n hydrolyysiin, mikä auttaa saavuttamaan vaaditun tiheyseron ilman, että kalvo saa vaarallisesti virtaa.
Termodynamiikan toinen laki opettaa meille, että yleensä konsentraatiogradienttien läsnäolo tyhjentyy lopulta massankuljetusprosesseilla, jotka ajavat systeemit tasaisesti kohti tasapainotilaa. Vaikka termodynamiikan toinen laki kertoo meille systeemin lopullisen tilan luonteen (esim. tasaiset pitoisuudet), se ei kuitenkaan kerro, kuinka kauan kestää saavuttaa tämä tila. Kalvot ovat kehittyneet muodostamaan erittäin tehokkaan esteen monien ioni- ja molekyylilajien spontaanille siirtymiselle. Arvioidaksemme pitoisuuksien tasaantumisen aikaskaalaa meidän on tunnettava massankuljetusnopeudet, jotka riippuvat keskeisistä materiaaliominaisuuksista, kuten diffuusiovakioista ja läpäisevyyksistä.
Erittäin menestyksekäs ”lakien” luokka, joka kuvaa sellaisten systeemien käyttäytymistä, jotka ovat kokeneet jonkinlaisen pienen poikkeaman tasapainosta, ovat lineaariset kuljetuslait. Näissä laeissa esitetään yksinkertainen lineaarinen suhde jonkin kiinnostavan suureen kulkeutumisnopeuden ja siihen liittyvän käyttövoiman välillä. Massan kulkeutumisessa on lineaarinen suhde virtauksen (eli pinta-alayksikköä kohti aikayksikköä kohti kulkevien molekyylien lukumäärä) ja konsentraatioeron (joka toimii vastaavana liikkeellepanevana voimana) välillä. Kalvojen läpi tapahtuvan kuljetuksen osalta nämä ajatukset on koodattu yksinkertaiseen yhtälöön (neutraalille liuenneelle aineelle) j= – p-(cin-cout), jossa j on soluun tuleva nettovirta, cin ja cout viittaavat konsentraatioihin kalvoon sidotun alueen sisä- ja ulkopuolella ja p on materiaaliparametri, jota kutsutaan permeabiliteetiksi. P:n yksiköt voidaan päätellä huomioimalla, että virtauksen yksikkönä on lukumäärä/(pinta-ala x aika) ja konsentraation yksikkönä on lukumäärä/tilavuus, mikä tarkoittaa, että itse p:n yksiköt ovat pituus/aika. Kuten monilla kuljetussuureilla (esim. materiaalien sähkönjohtavuudet, jotka vaihtelevat yli 30 suuruusluokkaa), läpäisevyydellä on hyvin suuri dynaaminen vaihteluväli, kuten kuvassa 1 on esitetty. Kuten kuvasta nähdään, lipidikaksoiskalvoilla on lähes 1010-kertainen permeabiliteettien vaihteluväli.
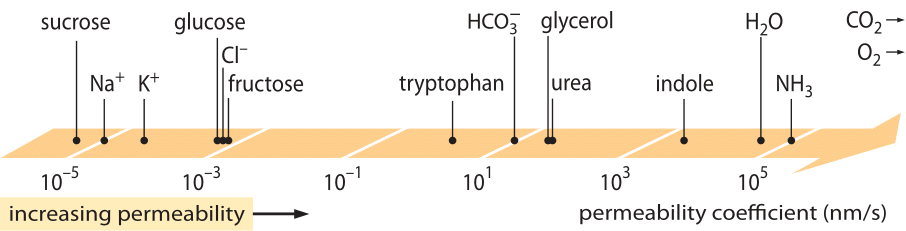
Kuva 1: Eri yhdisteiden kalvojen permeabiliteettien laaja vaihteluväli solussa. Kalvot ovat läpäisevämpiä varauksettomille yhdisteille ja vähiten läpäiseviä varatuille ioneille. Huomaa, että ionikanavien olemassaolo tekee näennäisestä läpäisevyydestä niiden ollessa auki useita kertaluokkia suuremman. Yksiköksi on valittu nm/s, ja useita nm on kalvon ominaisleveys. Kuva mukailtu lähteestä R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983. Glukoosin arvo on pienempi kuin Robertsonin arvo, joka perustuu useisiin lähteisiin, kuten BNID 110830, 110807. Muut tietolähteet: BNID 110729, 110731, 110816, 110824, 110806.
Mitkä fysikaalis-kemialliset parametrit ohjaavat yhdisteen sijoittumista läpäisevyysasteikolla? Yksi nyrkkisääntö on, että pienillä molekyyleillä on suuremmat läpäisevyydet kuin suuremmilla molekyyleillä. Toinen nyrkkisääntö on, että neutraalit yhdisteet voivat läpäistä kalvon monta kertaluokkaa nopeammin kuin samankaltaisesti varautuneet yhdisteet. Varautuneista yhdisteistä negatiivisilla (anionisilla) yhdisteillä on yleensä paljon suurempi läpäisevyys kuin positiivisilla (kationisilla) yhdisteillä. Ns. Overtonin säännön mukaan membraanin läpäisevyys kasvaa hydrofobisuuden kasvaessa, jolloin hydrofobisuus tarkoittaa yhdisteen taipumusta suosia poolitonta liuotinta polaarisen (vesiliuottimen) sijaan. Overtonin säännön mukaan varautuneilla (ei-hydrofobisilla) molekyyleillä, kuten ioneilla, on yleensä alhainen läpäisevyys, koska ne joutuvat kärsimään kalvon läpäisemisestä aiheutuvasta energiarangaistuksesta, kun taas liuenneilla kaasuilla, kuten O2:lla ja CO2:lla, jotka ovat hydrofobisia (koska ne ovat varauksettomia ja symmetrisiä), on korkea läpäisevyys. Lipidi-kaksoiskerroskalvojen läpäisevyys CO2:lle antaa todellakin arvoja, jotka ovat 0,01-1 cm/s (kyllä, läpäisevyysmittauksissa on hyvin suuria epävarmuuksia eri laboratorioiden välillä, BNID 110004, 110617, 102624), jotka ovat korkeampia kuin kaikki muut kuvassa 1 esitetyt arvot. Tämä arvo osoittaa, että solukalvon muodostama este on itse asiassa pienempi este kuin solukalvon ulkopuolelta solukalvoon tunkeutuvan sekoittumattoman vesikerroksen aiheuttama este. Tällainen päätelmä voidaan johtaa esteen läpäisykertoimen yhtälöstä, joka saadaan kaavalla p=K x D/l, jossa l on leveys, D diffuusiokerroin ja K jakokerroin väliaineen ja esteen materiaalin välillä. Tämä tunnetaan myös läpäisevyyden ”liukoisuus-diffuusio”-mallina, jossa nämä merkitsevät K- ja D-vaikutuksia, jotka ovat kaksi läpäisevyyteen vaikuttavaa vaihetta. Sekoittamattomalle vesikerrokselle K=1, koska se on hyvin samankaltainen kuin väliaine, mutta kalvoille arvo on yleensä useita kertaluokkia pienempi kuin 1 kaikille muille kuin kaikkein hydrofobisimmille materiaaleille. Tämä riippuvuus K:sta on edellä mainitun Overtonin säännön ydin. Hiilidioksidin suuri läpäisevyys viittaa myös siihen, että akvaporiinien kaltaisia kanavia, joiden oletettiin palvelevan kaasun kuljettamista soluun, ei tarvita, koska kalvo on riittävän läpäisevä. Nähdäksemme, miten kalvon ominaisuudet vaikuttavat aineenvaihduntatuotteiden kemialliseen koostumukseen, siirrymme laskemaan eri yhdisteiden vuotoaikoja
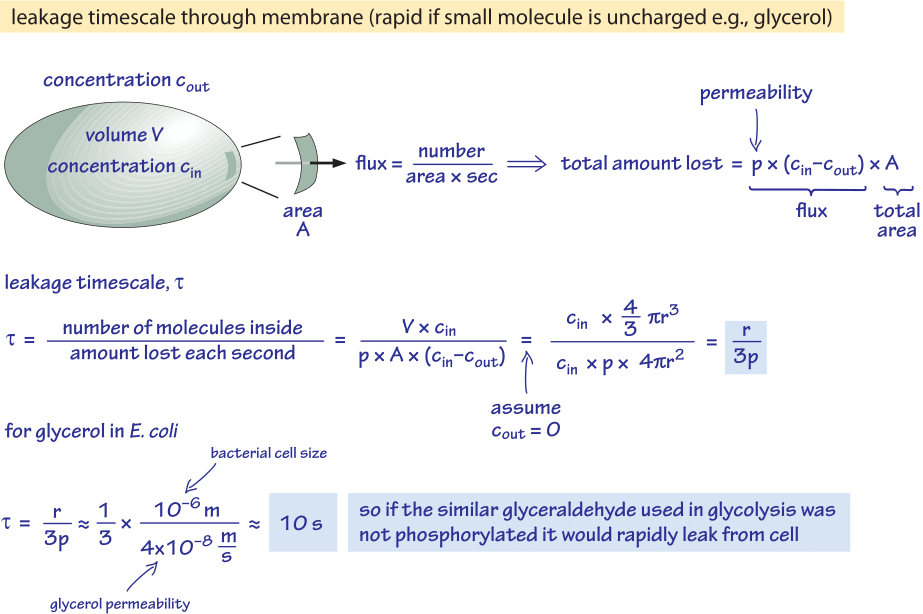
Kuva 2: Back of the envelope -laskelma ajasta, jonka kuluessa fosforyloimaton glukoosimolekyyli diffundoituu passiivisesti ulos bakteerisolusta. Tämän jälkeen tarkastellaan toiminnallisia vaikutuksia nopeasti kasvavaan soluun, jossa vaikutus on mitätön, ja stationaarisessa tilassa oleviin soluihin, joissa se voi aiheuttaa huomattavaa resurssien vuotoa.
Tarkastellaan esimerkiksi glyserolia. Kuvassa 2 esitetty analyysi antaa arvion ajasta, jolloin se vuotaa ulos solusta, jos molekyyliä ei fosforyloida tai muutoin muunneta hydrofiilisempään muotoon. Solukalvon läpäisevyys glyserolille on p≈10-100 nm/s (BNID 110824), kuten kuvasta 1 voidaan lukea. Aika, jonka kuluessa solun sisällä oleva glyserolimolekyyli poistuu takaisin ympäröivään väliaineeseen, kun oletetaan, että takaisinvirtausta soluun ei tapahdu (cout=0), voidaan karkeasti arvioida toteamalla, että ulosvirtaus solusta on p-A-cin, jossa A on solun pinta-ala. Aika-asteikko löytyy ottamalla solussa oleva kokonaismäärä V-cin (jossa V on solun tilavuus tai tarkemmin sanottuna solun vesitilavuus) ja jakamalla se tällä virtauksella, jolloin bakteerisolulle (r≈1 μm) saadaan aika-asteikko:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Tämä on karkea arvio, koska emme ottaneet huomioon cin-konsentraation pienenemistä ajan myötä, mikä antaa korjauskertoimeksi 1/ln(2), eli alle 2-kertaisen kasvun. Näistä arvioista opimme, että jos glykolyyttiset välituotteet glyseraldehydi tai dihydroksiasetoni, jotka ovat hyvin samankaltaisia kuin glyseroli, eivät fosforyloituisi, mikä johtaisi varauksen lisäämiseen, ne häviäisivät väliaineeseen diffuusiolla solukalvon läpi. Laboratorioympäristössä, jossa hiililähdettä syötetään runsaasti, tämä ei ole merkittävä ongelma, mutta luonnollisessa ympäristössä, jossa solut usein odottavat stationaarivaiheessa onnekasta ravinnepulssia (E. coli-kolibakteerin uskotaan käyvän läpi kuukausien kasvutauon sen jälkeen, kun se on eronnut elimistöstä, ennen kuin se löytää uuden isännän), solu voi hillitä häviöjään varmistamalla, että aineenvaihdunnan välituotteet on merkitty varauksella, joka estää niitä ylittämästä uudelleen lipidikaksoiskerroksen esittämää estettä.




