Kuvaamme kolme esimerkkiä biotieteistä: yhden fysiikasta, yhden genetiikkaan liittyvän ja yhden hiirikokeesta. Ne ovat hyvin erilaisia, mutta päädymme silti käyttämään samaa tilastollista tekniikkaa: lineaaristen mallien sovittamista. Lineaarisia malleja opetetaan ja kuvataan tyypillisesti matriisialgebran kielellä.
Motivoivat esimerkit
Putoavat kappaleet
Kuvittele, että olet Galilei 1500-luvulla ja yrität kuvata putoavan kappaleen nopeutta. Avustaja kiipeää Pisan torniin ja pudottaa pallon, kun taas useat muut avustajat kirjaavat sijainnin eri aikoina. Simuloidaan dataa käyttämällä nykyään tuntemiamme yhtälöitä ja lisäämällä siihen hieman mittausvirhettä:
set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##metersAsistajat ojentavat datan Galileolle, ja hän näkee seuraavaa:
mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")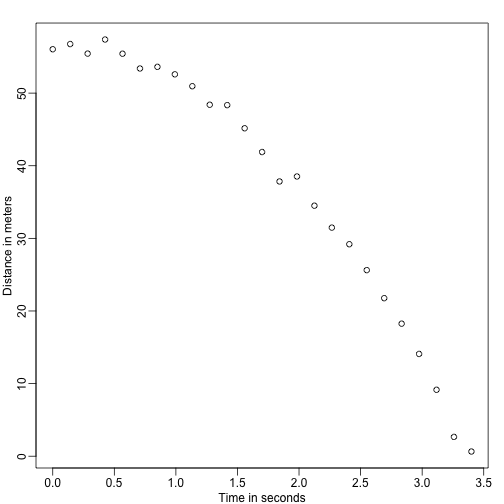
Hän ei tiedä tarkkaa yhtälöä, mutta katsomalla yllä olevaa kuvaajaa hän päättelee, että sijainnin pitäisi seurata paraabelia. Niinpä hän mallintaa datan:
With edustaa sijaintia, edustaa aikaa ja ottaa huomioon mittausvirheen. Tämä on lineaarinen malli, koska se on lineaarinen yhdistelmä tunnetuista suureista (th s), joita kutsutaan ennustajiksi tai kovariaateiksi, ja tuntemattomista parametreista (s).
Isän &pojan korkeudet
Kuvittele nyt olevasi Francis Galton 1800-luvulla ja kerääväsi parittaisia pituustietoja isiltä ja pojilta. Epäilet, että pituus periytyy. Aineistosi:
library(UsingR)x=father.son$fheighty=father.son$sheightnäyttää seuraavalta:
plot(x,y,xlab="Father's height",ylab="Son's height")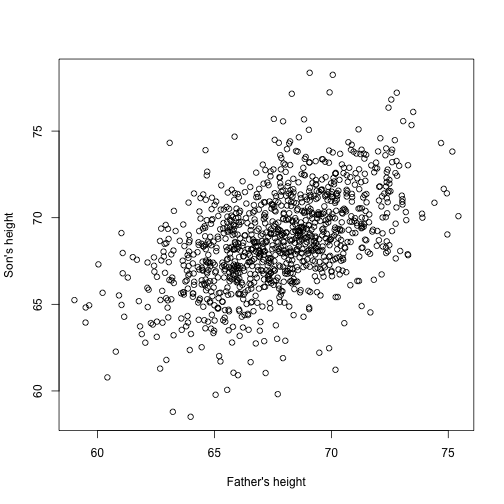
Poikien pituudet näyttävätkin kasvavan lineaarisesti isien pituuksien myötä. Tällöin aineistoa kuvaava malli on seuraava:
Tämäkin on lineaarinen malli, jossa on ja , isän ja pojan pituudet vastaavasti -luvun parille ja termi, joka ottaa huomioon ylimääräisen vaihtelun. Tässä ajattelemme, että isien pituudet ovat ennustaja ja että ne ovat kiinteitä (eivät satunnaisia), joten käytämme pienaakkosia. Pelkkä mittausvirhe ei voi selittää kaikkea vaihtelua, joka näkyy . Tämä on järkevää, koska mallissa ei ole muita muuttujia, esimerkiksi äitien pituudet, geneettinen satunnaisuus ja ympäristötekijät.
Sattumanvaraiset näytteet useista populaatioista
Tässä luemme sisään hiirten ruumiinpainotietoja hiiristä, joille oli syötetty kahta erilaista ruokavaliota: runsasrasvaista ruokavaliota ja kontrolliruokavaliota (chow). Meillä on kummastakin satunnaisotos, jossa on 12 hiirtä. Olemme kiinnostuneita selvittämään, onko ruokavaliolla vaikutusta painoon. Tässä on tiedot:
dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")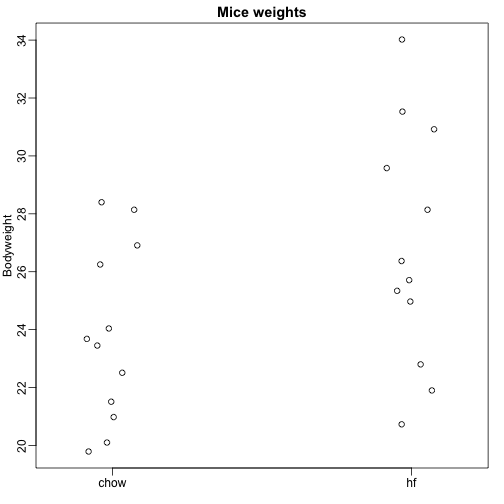
Haluamme arvioida populaatioiden välisen keskimääräisen painon eron. Osoitimme, miten tämä tehdään t-testien ja luottamusvälien avulla otoskeskiarvojen eron perusteella. Saamme täsmälleen samat tulokset käyttämällä lineaarista mallia:
keskipainon chow-ruokavaliolla, keskiarvojen eron, milloin hiiri saa runsasrasvaista (hf) ruokavaliota, milloin se saa chow-ruokavaliota, ja selittää saman populaation hiirten väliset erot.
Lineaariset mallit yleisesti
Olemme nähneet kolme hyvin erilaista esimerkkiä, joissa lineaarisia malleja voidaan käyttää. Yleinen malli, joka kattaa kaikki edellä mainitut esimerkit, on seuraava:
Huomaa, että meillä on yleinen määrä ennustajia . Matriisialgebra tarjoaa kompaktin kielen ja matemaattisen kehyksen, jonka avulla voidaan laskea ja tehdä johtopäätöksiä millä tahansa lineaarisella mallilla, joka sopii yllä olevaan kehykseen.
Parametrien estimointi
Jotta yllä olevat mallit olisivat käyttökelpoisia, meidän on estimoitava tuntemattomat s. Ensimmäisessä esimerkissä haluamme kuvata fysikaalista prosessia, jonka parametreja emme voi tuntea. Toisessa esimerkissä ymmärrämme paremmin periytymistä arvioimalla, kuinka paljon isän pituus keskimäärin vaikuttaa pojan pituuteen. Viimeisessä esimerkissä haluamme selvittää, onko eroa todella olemassa: jos .
Vakiintunut lähestymistapa tieteessä on löytää ne arvot, jotka minimoivat sovitetun mallin etäisyyden dataan. Seuraavaa kutsutaan pienimmän neliösumman (LS) yhtälöksi, ja tulemme näkemään sen usein tässä luvussa:
Kun löydämme minimin, kutsumme arvoja pienimmän neliösumman estimaateiksi (LSE, least squares estimates) ja merkitsemme niitä tunnuksella . Määrää, joka saadaan arvioitaessa pienimmän neliön yhtälöä estimaateilla, kutsutaan jäännösneliösummaksi (RSS). Koska kaikki nämä suureet riippuvat , ne ovat satunnaismuuttujia. S ovat satunnaismuuttujia, ja suoritamme lopulta päättelyn niille.
Putoavan kappaleen esimerkki uudelleen
Lukion fysiikanopettajani ansiosta tiedän, että putoavan kappaleen lentoradan yhtälö on:
jossa ja ovat vastaavasti lähtökorkeus ja nopeus. Edellä simuloimamme tiedot noudattivat tätä yhtälöä ja lisäsimme mittausvirheen simuloidaksemme n havaintoja pallon pudottamisesta Pisan tornista . Siksi käytimme tätä koodia simuloidaksemme dataa:
g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)Tältä data näyttää, kun yhtenäinen viiva edustaa todellista lentorataa:
plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)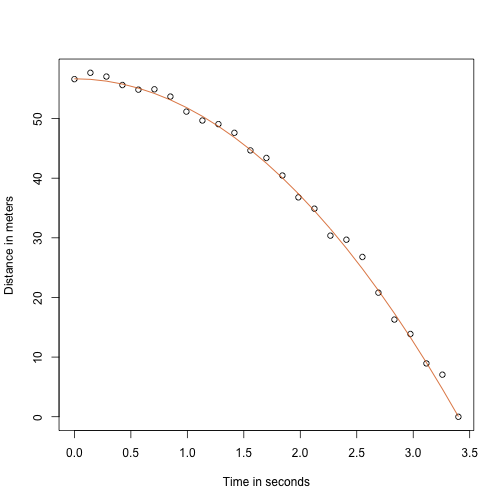
Mutta teeskentelimme olevamme Galilei, joten emme tiedä mallin parametreja. Datan perusteella se on kuitenkin paraabeli, joten mallinnamme sen sellaiseksi:
Miten löydämme LSE:
Funktiolla lm
R:ssä voimme sovittaa tämän mallin yksinkertaisesti käyttämällä lm-funktiota. Kuvaamme tätä funktiota yksityiskohtaisesti myöhemmin, mutta tässä on esimakua:
tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17Se antaa meille LSE:n sekä keskivirheet ja p-arvot.
Tämässä osiossa selitämme osittain tämän funktion taustalla olevaa matematiikkaa.
Vähimmän neliöiden estimaatti (LSE)
Kirjoitetaan funktio, joka laskee RSS:n mille tahansa vektorille :
rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}Siten mille tahansa kolmiulotteiselle vektorille saadaan RSS. Tässä on kuvaaja RSS:n funktiona, kun pidämme kaksi muuta kiinteänä:
Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)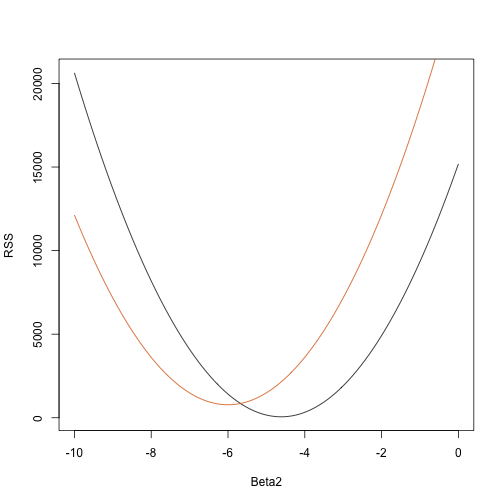
Kokeilu ja erehdys tässä ei tule toimimaan. Sen sijaan voimme käyttää laskutoimitusta: otetaan osittaisderivaatat, asetetaan ne arvoon 0 ja ratkaistaan. Tietenkin, jos meillä on monia parametreja, nämä yhtälöt voivat muuttua melko monimutkaisiksi. Lineaarialgebra tarjoaa kompaktin ja yleisen tavan ratkaista tämä ongelma.
Lisää Galtonista (Advanced)
Tutkittaessa isä-poika-aineistoa Galton teki kiehtovan havainnon käyttäen eksploratiivista analyysia.
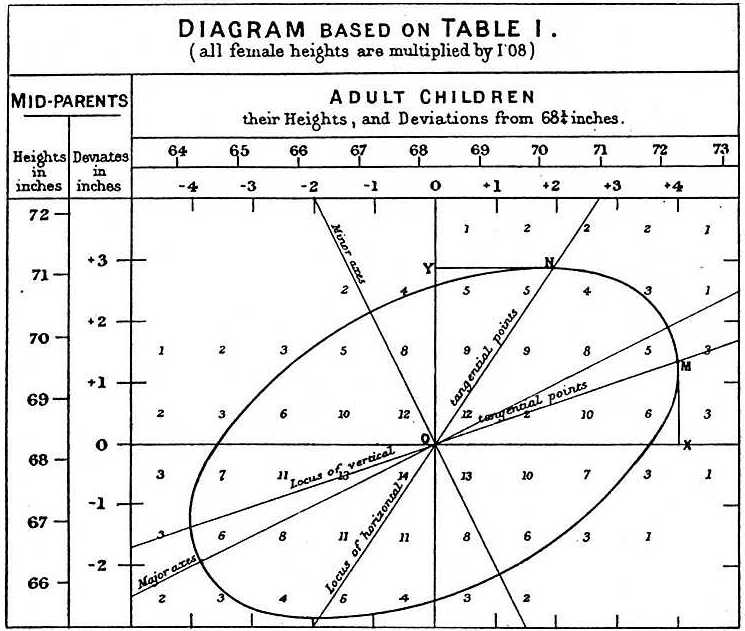
Hän huomasi, että jos hän taulukoi isä-poika-poika-korkeuslukuisten korkeuslukuisten mallien lukumäärän taulukkomuodossa ja seurasi taulukosta kaikkia x,y-arvoja, joilla oli samat loppusummamäärät, niin ne muodostivat ellipsin. Yllä olevassa Galtonin tekemässä kuvaajassa näet ellipsin, joka muodostuu pareista, joilla on 3 tapausta. Tämä johti sitten tämän datan mallintamiseen korreloituneena kaksimuuttujaisena normaalina, jota kuvailimme aiemmin:
Kuvailimme, miten voimme käyttää matematiikkaa osoittaaksemme, että jos pidät kiinteänä (ehto on ) jakauma on normaalijakautunut, jonka keskiarvo: ja keskihajonta . Huomaa, että on korrelaatio välillä ja , mikä merkitsee, että jos kiinnitämme , noudattaa itse asiassa lineaarista mallia. Yksinkertaisen lineaarisen mallimme parametrit ja voidaan ilmaista lausekkeina , ja .
.