Jos pidät juomasta, Klein-pullo ei ole suositeltava astia. Se saattaa näyttää epämääräisesti pullolta, mutta se ei sisällä mitään tilavuutta, mikä tarkoittaa, että siihen ei oikeastaan mahdu mitään nestettä. Mitä ikinä kaadatkaan ”sisään”, se tulee vain takaisin ulos.
Miten rakennat tuollaisen oudon kapineen ja miksi haluaisit rakentaa sen? Matemaatikko Felix Klein, joka löysi pullon vuonna 1882, kuvasi sitä pinnaksi, joka ”voidaan havainnollistaa kääntämällä kumiputken pala ylösalaisin ja antamalla sen kulkea itsensä läpi niin, että ulkopuoli ja sisäpuoli kohtaavat”.
Selaimesi ei tue videotunnistetta.Suora linkki
On selvää, että Kleinin pullo, aivan kuten tutumpi pallokin, on suljettu pinta: se on äärellinen siinä mielessä, että se mahtuu rajalliselle avaruusalueelle, mutta muurahainen voisi kävellä sen päällä ikuisesti törmäämättä koskaan rajaan tai putoamatta reunan yli. Toisin kuin pallolla, jolla on sisä- ja ulkopuoli, Klein-pullo on yksipuolinen: muurahainen voisi päästä pinnan jokaisen pisteen molemmille puolille. Tämän vuoksi pullo ei sisällä mitään tilavuutta, ja se vastaa myös kysymykseen ”miksi”: Kleinin pullo on mielenkiintoinen, koska emme tapaa luonnossa montaa yksipuolista muotoa. (Katso täältä toinen erittäin kaunis kuva Kleinin pullosta.)

Möbion kaistale on yksipuolinen – katso animaatio. (Kuva ja animaatio Konrad Polthier.)
Jos tämä on hieman hämmentävää, ajattele yksinkertaisempaa esimerkkiä yksipuolisesta pinnasta: kuuluisaa Möbius-nauhaa. Voit tehdä sellaisen ottamalla paperiliuskan kaksi päätä, kiertämällä liuskaa ja liimaamalla päät yhteen. Käyttämällä paperiliuskaa, jonka molemmilla puolilla on eri värit, esimerkiksi vihreä ja oranssi, on helppo uskotella itselleen, että tuloksena syntyvä Möbius-liuska on yksipuolinen. Kun olet kiertänyt ja liimannut, huomaat, että pääset jokaiseen oranssiin pisteeseen jokaisesta vihreästä pisteestä ilman, että sinun tarvitsee lävistää paperia tai kiivetä sen reunan yli.
Toisin kuin Kleinin pullolla, Möbius-nauhalla on raja – se muodostuu alkuperäisen nauhan kahdesta liimaamattomasta reunasta. Mutta näiden kahden välillä on yhteys. Jos otetaan kaksi Möbius-nauhaa ja luodaan suljettu muoto yhdistämällä niiden rajat tavallisella kaksipuolisella nauhalla, kuten alla on esitetty, saadaan täsmälleen Kleinin pullo.
Selaimesi ei tue videotunnistetta.Suora linkki
nauhalla, jonka taka- ja etupuoli on värjätty valkoiseksi ja etupuoli siniseksi. Konrad Polthierin animaatio.
Tämä tosiasia innoitti matemaatikko Leo Moserin kirjoittamaan limerikin:
Matemaatikko nimeltä KleinAjatteli Möbiusin nauhan olevan jumalallinen.Sanoi hän: ”
Jotkut matemaatikot ovat todella monilahjakkaita!
Kleinin pullon toinen erikoinen piirre on se, että se leikkaa itseään, mikä tarkoittaa, että sitä on vaikea tehdä yhdestä kumiputkesta, kuten Klein ehdotti. Tarkkaan ottaen yllä kuvattu itseään leikkaava objekti ei ole Kleinin pullo, vaan (kuten Klein viittasi) vain visualisointi sellaisesta. Ymmärtääksesi miksi, ajattele ensin tutumpaa donitsia (joka tunnetaan matemaattisesti nimellä torus). Toruksen voi tehdä neliönmuotoisesta kumilevystä liimaamalla ensin kaksi vastakkaista sivua sylinteriksi ja liimaamalla sitten tuon sylinterin kaksi reunaosaa toruksen saamiseksi.

Toruksen tekeminen: Liimaa ensin vastakkaiset pisteet neliön kahdelta vastakkaiselta sivulta muodostaaksesi sylinterin ja liimaa sitten tuon sylinterin kaksi rajakomponenttia (jotka vastaavat vastakkaisten pisteiden liimaamista neliön kahdelta jäljelle jäävältä sivulta) muodostaaksesi toruksen.
Jos et halua vaivautua liimaamiseen, voit yksinkertaisesti ajatella torusta neliönä pitäen mielessä, että vastakkaisten sivujen vastakkaiset pisteet katsotaan samoiksi. Kun siis liu’utat ”neliöön” piirrettyä muotoa yläreunan yli, se ilmestyy uudelleen alareunaan ja kun liu’utat sitä oikean reunan yli, se ilmestyy uudelleen vasempaan reunaan (ja päinvastoin).
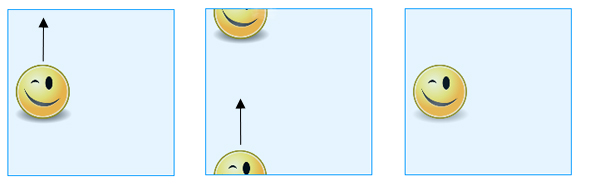
Kun liu’utat ”neliöön” piirrettyä muotoa yläreunan yli, se ilmestyy uudelleen alareunaan.
Todellisen Klein-pullon saamiseksi aloitetaan samalla tavalla tunnistamalla vastakkaiset kohdat neliön vastakkaisten sivujen parista. Toista sivuparia varten älä kuitenkaan tunnista suoraan vastakkaisia pisteitä, vaan diagonaalisesti vastakkaisia pisteitä, kuten kuvassa näkyy.
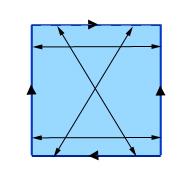
Klein-pullon tekeminen: tunnista kahden vastakkaisen sivun (tässä kuvassa pystysuorat sivut) vastakkaiset pisteet ja tunnista sitten diagonaalisesti vastakkaiset pisteet kahdelta muulta sivulta. (Jos merkitset ylä- ja alapuolen pisteet vasemmalta oikealle numeroilla 0-1, niin yläpuolen piste, jolla on merkintä x, tunnistetaan alapuolen pisteen kanssa, jolla on merkintä 1-x.)
Tuloksena saadaan Kleinin pullo. Voit taas ajatella sitä neliönä, pitäen mielessä, mitkä rajapisteet katsotaan samoiksi. Jos liu’utat muodon yhden reunan yli, jonka vastakkaiset pisteet on tunnistettu (kuvassamme pystysuora), se ilmestyy uudelleen vastakkaiselle puolelle, kuten aiemmin. Jos sitä kuitenkin liu’utetaan sellaisen reunan yli, jonka pisteet on tunnistettu diagonaalisesti (kuvassamme vaakasuorassa), se ilmestyy vastakkaiselle puolelle, mutta siirtyneenä ja alkuperäisen itsensä peilikuvana.
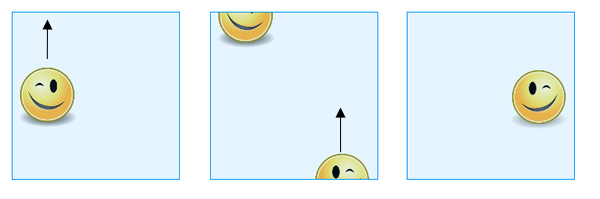
Jos muoto liu’utetaan yläreunan yli, se ilmestyy alareunan yli, mutta toiselle puolelle ja peilikuvana alkuperäisestä itsestään.
Ainut tapa rakentaa tämä muoto kolmiulotteiseen avaruuteen oikeasti liimaamalla pisteitä toisiinsa on sallia muodon leikata itsensä. Tämä tarkoittaa alkuperäisen neliön sisäpuolella olevien pisteparien tunnistamista, joten tarkkaan ottaen tuloksena oleva muoto ei ole täsmälleen sama kuin Kleinin pullo, jossa on tunnistettu vain rajapisteet. Se on vain yksi tapa esittää pullo kolmiulotteisessa avaruudessa (on muitakin).
Selaimesi ei tue videotunnistetta.suora linkki
Peilikuva ja orientoituvuus. Konrad Polthierin animaatio.
Kummallista kyllä, käsitteet ”sisällä”, ”ulkona” ja ”yksipuolisuus” riippuvat ympäristön tilasta, jossa esine istuu. Esimerkiksi paperille piirretyllä silmukalla (kaksiulotteisessa avaruudessa) on hyvin määritellyt sisä- ja ulkopuoli, mutta kolmiulotteiseen avaruuteen piirretyllä silmukalla ei ole. Tämän vuoksi emme voi puhua yksipuolisuudesta, ellemme ensin päätä, miten pinta upotetaan kolmiulotteiseen avaruuteen. On kuitenkin olemassa läheisesti siihen liittyvä ominaisuus, joka on muodolle ominainen eikä riipu ympäröivästä avaruudesta. Pintaa kutsutaan suunnattavaksi, jos siihen piirrettyä muotoa ei voi liu’uttaa ympäri ja takaisin sinne, mistä se lähti liikkeelle, niin että se näyttää omalta peilikuvaltaan. Kuten oikealla olevaan kuvaan liittyvästä animaatiosta näkyy, Möbius-nauha ei ole orientoituva. Ja kuten yläpuolella olevasta kuvasta, jossa on hymiö, näkyy, Kleinin pullo ei myöskään ole.Täydellisen matemaattisen kuvauksen antamiseksi Kleinin pullo on suljettu, ei-suuntautumiskykyinen pinta. Jos haluat lisätietoja siitä, katso artikkeli Kleinin pullon sisällä.
Tietoa kirjoittajasta
Marianne Freiberger on Plus-lehden päätoimittaja.