Tässä jaksossa tarkastellaan dipoliantennia, jonka säde on hyvin ohut. Dipoliantenni on samanlainen kuin lyhyt dipoli, paitsi että sen ei tarvitse olla pieni verrattuna aallonpituuteen (taajuudella, jolla antenni toimii).
Pituudeltaan L dipoliantennille, joka on suunnattu z-akselin suuntaisesti ja jonka keskipiste on z=0, virta kulkee z-suunnassa amplitudilla, joka noudattaa tarkasti seuraavaa funktiota:
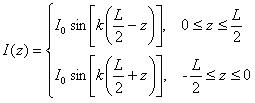
Huomaa, että myös tämä virta värähtelee ajassa sinimuotoisesti taajuudella f.Virtajakaumat neljänneksen aallonpituuden (vasen puolikas) ja täysipituisen aallonpituuden (oikea puolikas) dipoliantenneille on esitetty kuvassa 1. Huomaa, että virran huippuarvoa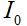 
ei saavuteta dipolin varrella, ellei pituus ole suurempi kuin puoli aallonpituutta.
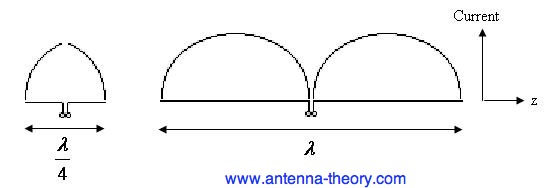
Kuva 1. Virtajakaumat äärellisen pituisissa dipoliantenneissa.
Ennen kuin tarkastellaan dipoliantennin säteilemiä kenttiä, tarkastellaan dipolin tuloimpedanssia sen pituuden funktiona, joka on piirretty alla olevassa kuvassa 2. Huomaa, että tuloimpedanssi on määritelty kaavalla Z=R + jX, jossa R on resistanssi ja X on reaktanssi.
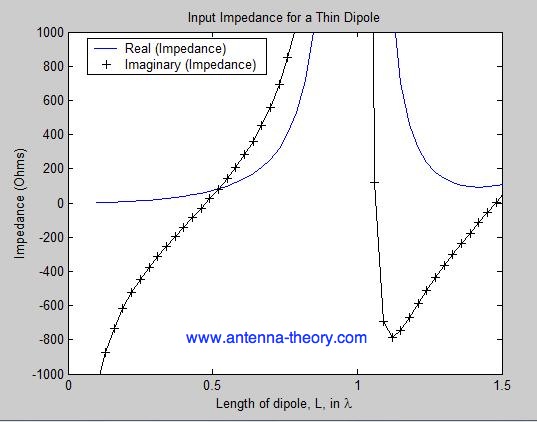
Kuva 2. Tuloimpedanssi dipoliantennin pituuden (L) funktiona.
Huomaa, että hyvin pienillä dipoliantenneilla tuloimpedanssi on kapasitiivinen, mikä tarkoittaa, että impedanssia hallitsee negatiivinen reaktanssiarvo (ja suhteellisen pieni reaaliimpedanssi tai resistanssi). Kun dipoli kasvaa, sisääntulovastus kasvaa reaktanssin ohella. Hieman alle 0,5 
antennin impedanssin imaginaarikomponentti on nolla (reaktanssi X=0), ja antennin sanotaan olevan resonanssissa.
Jos dipoliantennin pituus tulee lähelle yhtä aallonpituutta, tuloimpedanssista tulee ääretön. Tätä hurjaa tuloimpedanssin muutosta voidaan ymmärtää opiskelemalla korkeataajuisten siirtojohtojen teoriaa. Yksinkertaisempana selityksenä voidaan tarkastella kuvassa 1 esitettyä yhden aallonpituuden dipolia. Jos kuvan 1 oikeanpuoleisen antennin liittimiin kytketään jännite, virran jakautuminen on kuvan mukainen. Koska virta liittimissä on nolla, tuloimpedanssi (Z=V/I) on välttämättä ääretön. Näin ollen ääretön impedanssi esiintyy aina, kun dipoliantenni on aallonpituuden kokonaislukukertainen kerrannainen.
Seuraavassa luvussa tarkastelemme dipoliantennien säteilykuviota.
Dipoliantennien säteilykuviot
Pituudeltaan L olevan dipoliantennin kaukokentät saadaan:
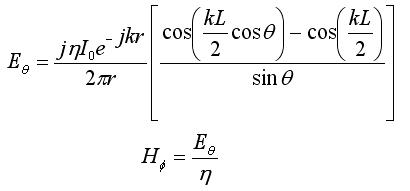
Kuvassa 3 on esitetty normalisoidut säteilykuviot pituudeltaan eripituisille dipoliantenneille.
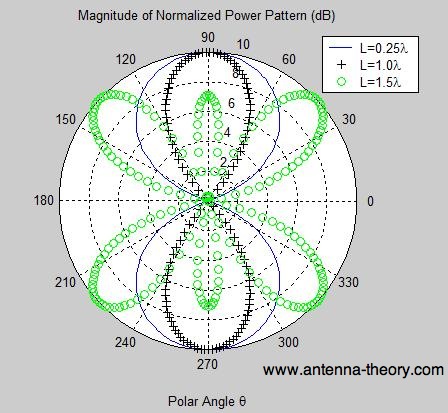
Kuva 3. Dipoliantennien säteilykuviot. Normalisoidut säteilykuviot tietyn pituisille dipoliantenneille.
Täyden aallonpituuden dipoliantenni on suuntaavampi kuin lyhyempi neljänneksen aallonpituuden dipoliantenni. Tämä on tyypillinen tulos antenniteoriassa: Suuntaavuuden lisäämiseksi tarvitaan yleensä suurempi antenni. Tulokset eivät kuitenkaan aina ole ilmeisiä. Kuvaan 3 on piirretty myös 1,5 aallonpituuden dipolikuvio. Huomaa, että tämä kuvio on suurimmillaan noin +45 ja -45 asteessa.
Dipoliantenni on symmetrinen atsimutaalisesti (dipolin pitkän akselin ympäri) katsottuna; tämän seurauksena säteilykuvio ei ole atsimutaalikulman 
funktio. Näin ollen dipoliantenni on esimerkki ympärisäteilevästä antennista. Lisäksi E-kentällä on vain yksi vektorikomponentti ja näin ollen kentät ovat lineaarisesti polarisoituneita. Tarkasteltaessa x-y-tasossa (z-akselin suuntaisen dipolin tapauksessa) E-kenttä on -y-suuntainen, ja näin ollen dipoliantenni on vertikaalisesti polarisoitunut.
Kuvassa 4 on esitetty yhden aallonpituuden dipoliantennin 3D-kuvio. Tämä kuvio on samanlainen kuin neljännes- ja puoliaaltodipoliantennin kuvio.
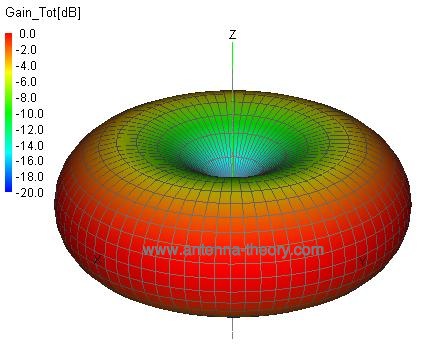
Kuva 4. Normalisoitu 3d-säteilykuvio yhden aallonpituuden dipoliantennille.
1,5 aallonpituuden dipoliantennin 3d-säteilykuvio on huomattavasti erilainen, ja se on esitetty kuvassa 5.
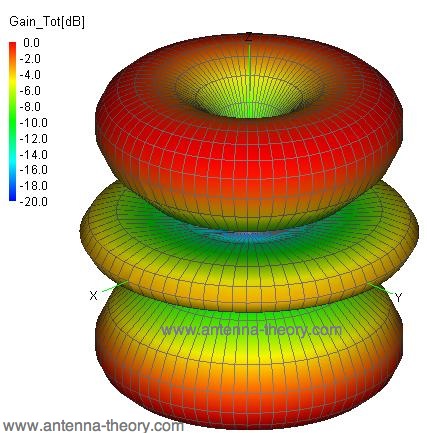
Kuva 5. Normalisoitu 3d-säteilykuvio 1,5 aallonpituuden dipoliantennille.
Dipoliantennin (huippu)suuntaavuus vaihtelee kuvan 6 mukaisesti.
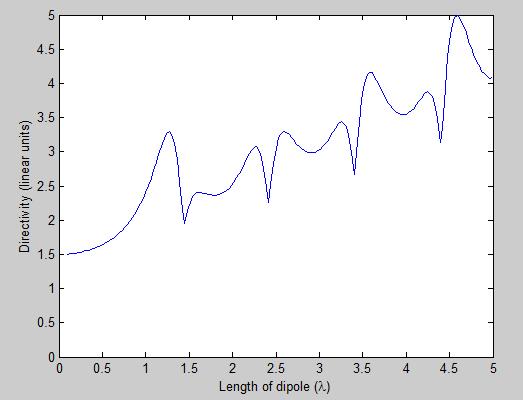
Kuva 6. Dipoliantennin suuntaavuus dipolin pituuden funktiona.
Kuvasta 6 nähdään, että noin L=1,25:een asti suuntaavuus kasvaa pituuden myötä. Pidemmillä pituuksilla suuntaavuudella on kuitenkin nouseva suuntaus, mutta se ei ole enää monotoninen.
Seuraavassa kappaleessa tarkastellaan yleisintä dipoliantennia, puoliaaltodipoliantennia.
Seuraava: Puoliaaltodipoliantennit
Ylös: Antennas List
Antennas List
Antennateoria .com