Arktangenttitaulukko
| y | x = arctan(y) | |
|---|---|---|
| astetta | radiaania | |
| -1.732050808 | -60° | -π/3 |
| -1 | -45° | -π/4 |
| -0.577350269 | -30° | -π/6 |
| 0 | 0° | 0 |
| 0.577350269 | 30° | π/6 |
| 1 | 45° | π/4 |
| 1.732050808 | 60° | π/3 |
Mikä on 0:n arktangentti ?
arctan 0 = ?
Arktangentti on käänteinen tangenttifunktio.
Sence, tan 0 = tan 0º = 0
Osa 0:n arktangentti on yhtä suuri kuin 0:n käänteinen tangenttifunktio, joka on yhtä suuri kuin 0 radiaania tai 0 astetta:
arctan 0 = tan-1 0 = 0 rad = 0º
Mikä on 1:n arktangentti ?
arctan 1 = ?
Arctangentti on käänteinen tangenttifunktio.
Jos tan π/4 = tan 45º = 1
Ykkösen 1 arktangentti on yhtä suuri kuin 1:n käänteinen tangenttifunktio, joka on yhtä suuri kuin π/4 radiaania eli 45 astetta:
arctan 1 = tan-1 1 = π/4 rad = 45º
Mikä on 2:n arktangentti ?
arctan 2 = ?
Arctangentti on käänteinen tangenttifunktio.
Since, tan 1.107 = tan 63.435º = 2
Since, tan 1.107 = tan 63.435º = 2
Since 2:n arctangentti on yhtä suuri kuin käänteinen tangenttifunktio 2:n, joka on yhtä suuri kuin 1.107 radiaania eli 63,435 astetta:
arctan 2 = tan-1 2 = 1,107 rad = 63,435º
Äärettömän arctan
Mikä on äärettömän ja miinus äärettömän arctangentti?
arctan(∞) = ?
Arctangentti on käänteinen tangenttifunktio.
X:n arktangentin raja-arvo, kun x lähestyy ääretöntä, on yhtä suuri kuin pi/2 radiaania eli 90 astetta:
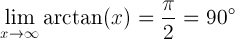
X:n arktangentin raja-arvo, kun x lähestyy miinus ääretöntä, on yhtä suuri kuin -pi/2 radiaania eli -90 astetta: 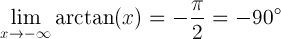
Arctanin derivaatta
Mikä on x:n arktangentin funktion derivaatta?
X:n arktangenttifunktion derivaatta on yhtä suuri kuin 1 jaettuna (1+x2)
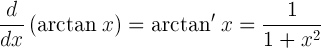
Arctanin integraali
Mikä on x:n arktangenttifunktion integraali?
X:n arktangenttifunktion epämääräinen integraali on:

Arctanin kuvaaja
X:n arktangentin kuvaaja: 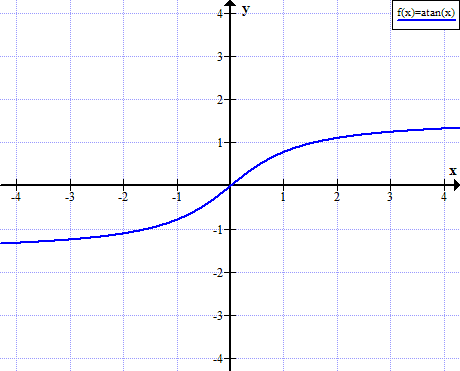
Mikä on arctan(x)
sin( arctan(x) ) = ?
X:n arktangentin sini on:
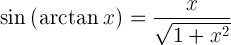
Mikä on arctan(x)
cos( arctan(x) ) = ?
X:n arktangentin kosini on:
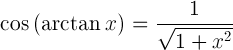 .
.