Voidaan Gibbs-Helmholtzin avulla saada \(K\)
\}{∂T} lämpötilariippuvuus
\}{∂T} \right)_P = \dfrac{-Δ_rH^o}{T^2}\]
Tasapainossa voimme rinnastaa \(Δ_rG^o\) \(-RT\ln K\), joten saamme:
\}{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2} \]
Me näemme, että se, kasvaako vai pieneneekö \(K\) lämpötilan myötä, liittyy siihen, onko reaktioentalpia positiivinen vai negatiivinen. Jos lämpötilaa muutetaan niin vähän, että \(Δ_rH^o\) voidaan pitää vakiona, voimme kääntää \(K\)-arvon yhdessä lämpötilassa toiseen lämpötilaan integroimalla edellä olevan lausekkeen, saamme samanlaisen derivaation kuin sulamispisteen aleneman kohdalla:
\
Jos tarvitaan enemmän tarkkuutta, voimme korjata ΔrHo:n lämpötilamuutokset käyttämällä lämpökapasiteettitietoja.
Miten \(K\) kasvaa tai pienenee lämpötilan mukana, liittyy siihen, onko reaktioentalpia positiivinen vai negatiivinen.
Yhtälön \(K\) lauseke on melko herkkä lämpötilan funktio, kun otetaan huomioon sen eksponentiaalinen riippuvuus stökiometristen kertoimien erosta Yksi tapa nähdä tasapainovakioiden herkkä lämpötilariippuvuus on muistaa, että
\
However, koska vakiopaineessa ja -lämpötilassa
\
Yhtälöstä \(\ref{18}\) tulee
\
Valitsemalla molempien puolien luonnollinen logaritmi saadaan lineaarinen suhde \(\ln K \)ja vakioentalpioiden ja -entropioiden välille:
\
joka tunnetaan nimellä van’t Hoffin yhtälö. Se osoittaa, että \(\ln K\) vs. \(1/T\) kuvaajan pitäisi olla viiva, jonka kaltevuus on \(-\Delta_r{H^o}/R\) ja leikkauspiste \(\Delta_r{S^o}/R\).
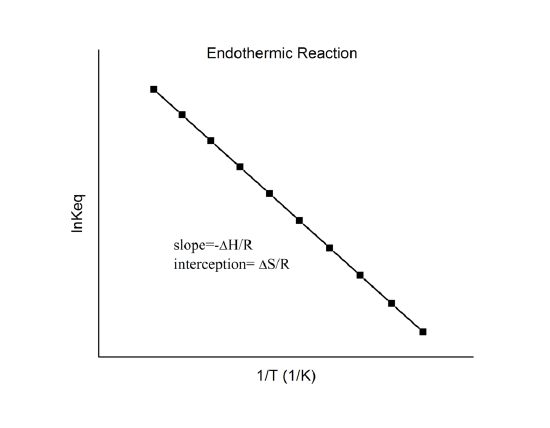
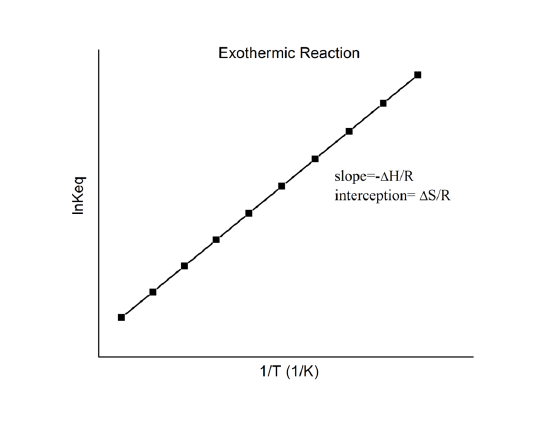
Siten nämä suureet voidaan määrittää \(\ln K\) vs. \(1/T\) -datasta tekemättä kalorimetriaa. Tärkein oletus tässä on tietenkin se, että \(\Delta_r{H^o}\) ja \(\Delta_r{S^o}\) ovat vain hyvin heikosti riippuvaisia \(T\):stä, mikä yleensä pitää paikkansa.