Was ist die Permeabilität der Zellmembran?
Lesemodus
Eines der charakteristischen Merkmale aller lebenden Organismen ist, dass sie eine unverwechselbare Mischung aus Ionen und kleinen Molekülen enthalten. Die Zusammensetzung unterscheidet sich nicht nur von der Umgebung, sondern kann auch innerhalb der Zelle variieren. So kann die Wasserstoffionenkonzentration in einigen Zellkompartimenten 104-mal höher sein als in anderen (die Mitochondrien erreichen einen pH-Wert von bis zu 8, die Lysosomen einen pH-Wert von bis zu 4, BNID 107521, 106074). Das Verhältnis der Konzentrationen von Ca2+-Ionen in den extra- und intrazellulären Flüssigkeitskompartimenten kann wiederum das 104-fache betragen (BNID 104083). Dieser Konzentrationsunterschied ist so groß, dass der Transport eines Ca2+-Ions durch die Membran vom intra- zum extrazellulären Kompartiment die Energie von mehr als einem Proton oder Natriumion erfordert, das den Protonen-Motivationsgradienten hinunterfließt. Um dies zu erkennen, sollte sich der Leser an die Faustregel aus unserer Liste der Tricks und Kniffe erinnern, wonach für den Aufbau einer Potenzialdifferenz in der Größenordnung 6 kJ/mol (≈2 kBT) erforderlich sind. Diese Energie kann z. B. durch den Transport einer elektrischen Ladung durch eine Potentialdifferenz von 60 mV erreicht werden. Um ein Konzentrationsverhältnis von vier Größenordnungen zu erreichen, müsste eine Ladung etwa 240 mV an Elektronenantriebskraft überwinden (wegen der doppelten Ladung des Calciumions sogar noch mehr). Dies liegt sehr nahe an der Durchbruchsspannung der Membran, wie in der Vignette „Wie groß ist die elektrische Potenzialdifferenz an Membranen?“ beschrieben. Das hohe Konzentrationsverhältnis von Ca2+ wird in der Regel durch Kopplung an den Transport von drei Natriumionen oder die Hydrolyse von ATP erreicht, wodurch die erforderliche Dichtedifferenz erreicht wird, ohne die Membran gefährlich zu erregen.
Der zweite Hauptsatz der Thermodynamik lehrt uns, dass im Allgemeinen das Vorhandensein von Konzentrationsgradienten schließlich durch Massentransportprozesse ausgeglichen wird, die Systeme stetig in einen Gleichgewichtszustand bringen. Der zweite Hauptsatz der Thermodynamik sagt uns zwar, wie der Endzustand eines Systems aussieht (z. B. gleichmäßige Konzentrationen), aber nicht, wie lange es dauern wird, bis dieser Zustand erreicht ist. Membranen haben sich so entwickelt, dass sie eine sehr effektive Barriere für den spontanen Transfer vieler ionischer und molekularer Spezies bilden. Um die Zeitskala für den Konzentrationsausgleich abzuschätzen, müssen wir die Massentransportraten kennen, die von wichtigen Materialeigenschaften wie Diffusionskonstanten und Permeabilitäten abhängen.
Eine sehr erfolgreiche Klasse von „Gesetzen“, die das Verhalten von Systemen beschreiben, die eine kleine Abweichung vom Gleichgewicht erfahren haben, sind die linearen Transportgesetze. Diese Gesetze gehen von einer einfachen linearen Beziehung zwischen der Transportrate einer bestimmten Menge von Interesse und der zugehörigen Antriebskraft aus. Beim Massentransport gibt es eine lineare Beziehung zwischen dem Fluss (d. h. der Anzahl der Moleküle, die eine Flächeneinheit pro Zeiteinheit durchqueren) und dem Konzentrationsunterschied (der als treibende Kraft dient). Für den Transport durch Membranen wurden diese Ideen in der einfachen Gleichung (für neutrale gelöste Stoffe) j= – p-(cin-cout) kodifiziert, wobei j der Nettofluss in die Zelle ist, cin und cout sich auf die Konzentrationen auf der Innen- und Außenseite der membrangebundenen Region beziehen und p ein Materialparameter ist, der als Permeabilität bezeichnet wird. Die Einheiten von p lassen sich ableiten, indem man feststellt, dass der Fluss die Einheiten Zahl/(Fläche x Zeit) und die Konzentration die Einheiten Zahl/Volumen hat, was bedeutet, dass die Einheiten von p selbst Länge/Zeit sind. Wie viele Transportgrößen (z. B. die elektrischen Leitfähigkeiten von Materialien, die sich über 30 Größenordnungen erstrecken) hat auch die Permeabilität einen sehr großen dynamischen Bereich, wie in Abbildung 1 dargestellt. Wie in der Abbildung zu sehen ist, weisen Lipiddoppelschichten einen fast 1010-fachen Bereich von Permeabilitäten auf.
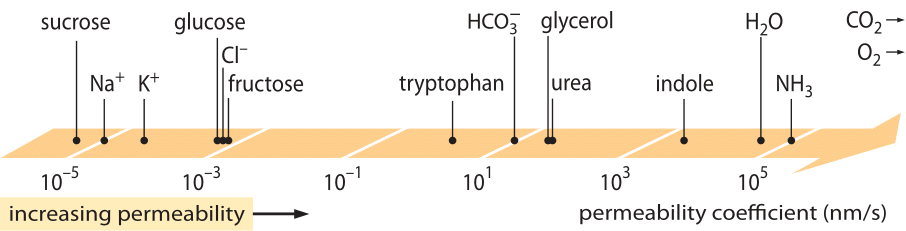
Abbildung 1: Der große Bereich von Membranpermeabilitäten verschiedener Verbindungen in der Zelle. Die Membranen sind für ungeladene Verbindungen durchlässiger und für geladene Ionen am wenigsten durchlässig. Es ist zu beachten, dass das Vorhandensein von Ionenkanälen die scheinbare Permeabilität um mehrere Größenordnungen erhöht, wenn diese geöffnet sind. Die Einheiten sind in nm/s angegeben, und einige nm sind die charakteristische Membranbreite. Die Abbildung wurde von R. N. Robertson, The Lively Membranes, Cambridge University Press, 1983, übernommen. Der Wert für Glukose ist kleiner als bei Robertson und basiert auf mehreren Quellen wie BNID 110830, 110807. Andere Quellen für Daten: BNID 110729, 110731, 110816, 110824, 110806.
Welche physikalisch-chemischen Parameter sind ausschlaggebend für die Platzierung einer Verbindung auf dieser Skala der Permeabilitäten? Eine Faustregel besagt, dass kleine Moleküle höhere Permeabilitäten haben als größere Moleküle. Eine andere Faustregel besagt, dass neutrale Verbindungen die Membran um viele Größenordnungen schneller passieren können als ähnlich geladene Verbindungen. Unter den geladenen Verbindungen haben negative (anionische) Verbindungen tendenziell eine viel höhere Durchlässigkeit als positive (kationische) Verbindungen. Die so genannte Overton-Regel besagt, dass die Membranpermeabilität mit der Hydrophobie zunimmt, wobei die Hydrophobie die Tendenz einer Verbindung ist, ein unpolares Lösungsmittel einem polaren (wässrigen) Lösungsmittel vorzuziehen. Die Overton-Regel besagt, dass geladene (nicht hydrophobe) Moleküle wie Ionen eher eine geringe Permeabilität aufweisen, da sie beim Durchdringen der Membran einen energetischen Nachteil erleiden, während gelöste Gase wie O2 und CO2, die hydrophob sind (da sie ungeladen und symmetrisch sind), eine hohe Permeabilität aufweisen. Die Permeabilität von Lipid-Doppelschichtmembranen für CO2 ergibt Werte von 0,01-1 cm/s (ja, Permeabilitätsmessungen haben sehr hohe Unsicherheiten zwischen verschiedenen Labors, BNID 110004, 110617, 102624), die höher sind als alle anderen in Abbildung 1 dargestellten Werte. Dieser Wert zeigt, dass die von der Zellmembran geschaffene Barriere tatsächlich ein geringeres Hindernis darstellt als die Barriere, die durch die nicht aufgewühlte Wasserschicht entsteht, die die Zellmembran von außen umschließt. Eine solche Schlussfolgerung lässt sich aus der Gleichung für den Permeabilitätskoeffizienten eines Hindernisses ableiten, die durch p=K x D/l gegeben ist, wobei l die Breite, D der Diffusionskoeffizient und K der Verteilungskoeffizient zwischen dem Medium und dem Hindernismaterial ist. Dies wird auch als „Löslichkeits-Diffusions“-Modell für die Permeabilität bezeichnet, wobei die Effekte K und D zwei Schritte darstellen, die die Permeabilität beeinflussen. Für eine ungerührte Wasserschicht ist K = 1, da sie dem Medium sehr ähnlich ist, aber für eine Membran ist der Wert für alle außer dem hydrophobsten Material in der Regel um mehrere Größenordnungen kleiner als 1. Diese Abhängigkeit von K ist der Kern der oben erwähnten Overton-Regel. Die hohe Durchlässigkeit für CO2 deutet auch darauf hin, dass Kanäle wie Aquaporine, die für den Gastransport in die Zelle vorgeschlagen wurden, nicht erforderlich sind, da die Membran durchlässig genug ist. Um zu sehen, wie sich die Membraneigenschaften auf die chemische Zusammensetzung der Metaboliten auswirken, berechnen wir die Leckagezeit für verschiedene Verbindungen
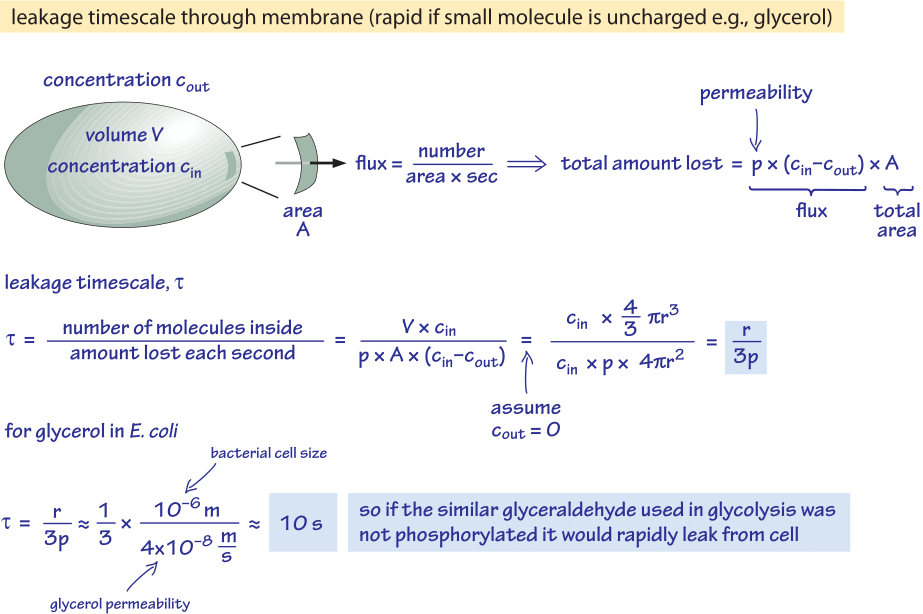
Abbildung 2: Rückwärtsberechnung der Zeitspanne, in der ein unphosphoryliertes Glukosemolekül passiv aus einer Bakterienzelle diffundiert. Die funktionellen Auswirkungen werden dann für schnell wachsende Zellen betrachtet, bei denen der Effekt vernachlässigbar ist, und für Zellen im stationären Zustand, bei denen es zu einem beträchtlichen Verlust von Ressourcen kommen kann.
Betrachten wir zum Beispiel Glycerin. Die in Abbildung 2 gezeigte Analyse gibt eine Schätzung für die Zeit, in der es aus der Zelle entweicht, wenn das Molekül nicht phosphoryliert oder anderweitig in eine hydrophilere Form umgewandelt wird. Die Permeabilität der Zellmembran für Glycerin beträgt p≈10-100 nm/s (BNID 110824), wie in Abbildung 1 zu sehen ist. Die Zeitskala, die ein Glycerinmolekül in der Zelle benötigt, um zurück in das umgebende Medium zu entweichen, lässt sich grob abschätzen, wenn man davon ausgeht, dass kein Rückfluss in die Zelle stattfindet (cout=0), da der Ausfluss aus der Zelle p-A-cin ist, wobei A die Zelloberfläche ist. Die Zeitskala wird ermittelt, indem man die Gesamtmenge in der Zelle, V-cin (wobei V das Zellvolumen oder genauer das Zellwasservolumen ist), nimmt und durch diesen Fluss dividiert, was für eine Bakterienzelle (r≈1 μm) eine Zeitskala ergibt:
t =V-cin/p-A-cin =(4πr3/3)/(4πr2-3×10-6 cm/s) ≈ 10 s.
Dies ist eine grobe Schätzung, weil wir die mit der Zeit abnehmende Konzentration von cin nicht berücksichtigt haben, die einen Korrekturfaktor von 1/ln(2) ergibt, d.h. weniger als eine 2-fache Zunahme. Aus diesen Schätzungen geht hervor, dass die glykolytischen Zwischenprodukte Glyceraldehyd oder Dihydroxyaceton, die dem Glycerin sehr ähnlich sind, durch Diffusion durch die Zellmembran an das Medium verloren gehen würden, wenn sie nicht phosphoryliert würden, was zu einer zusätzlichen Ladung führen würde. In Labormedien, in denen eine Kohlenstoffquelle im Überfluss vorhanden ist, ist dies kein großes Problem, aber in einer natürlichen Umgebung, in der die Zellen oft in der stationären Phase auf einen glücklichen Impuls von Nährstoffen warten (E. coli kann nach seiner Ausscheidung aus dem Körper monatelang nicht wachsen, bevor es einen neuen Wirt findet), kann die Zelle ihre Verluste eindämmen, indem sie dafür sorgt, dass Stoffwechselzwischenprodukte mit einer Ladung versehen werden, die sie daran hindert, die Barriere der Lipiddoppelschicht erneut zu überwinden.




