Last Updated on August 18, 2020
Datensätze können fehlende Werte enthalten, was für viele Algorithmen des maschinellen Lernens problematisch sein kann.
Es ist daher eine gute Praxis, fehlende Werte für jede Spalte in Ihren Eingabedaten vor der Modellierung Ihrer Vorhersageaufgabe zu identifizieren und zu ersetzen. Dies wird als Imputation fehlender Daten oder kurz als Imputation bezeichnet.
Ein beliebter Ansatz für die Imputation von Daten ist die Berechnung eines statistischen Wertes für jede Spalte (z. B. eines Mittelwerts) und die Ersetzung aller fehlenden Werte für diese Spalte durch den statistischen Wert. Es ist ein beliebter Ansatz, weil die Statistik mit dem Trainingsdatensatz einfach zu berechnen ist und weil er oft zu einer guten Leistung führt.
In diesem Tutorial erfahren Sie, wie Sie statistische Imputationsstrategien für fehlende Daten beim maschinellen Lernen verwenden können.
Nach Abschluss dieses Tutorials wissen Sie:
- Fehlende Werte müssen mit NaN-Werten markiert werden und können durch statistische Maße ersetzt werden, um die Spalte der Werte zu berechnen.
- Wie man einen CSV-Wert mit fehlenden Werten lädt und die fehlenden Werte mit NaN-Werten markiert und die Anzahl und den Prozentsatz der fehlenden Werte für jede Spalte angibt.
- Wie man fehlende Werte mit Statistiken als Datenaufbereitungsmethode bei der Bewertung von Modellen und bei der Anpassung eines endgültigen Modells ersetzt, um Vorhersagen für neue Daten zu treffen.
Starten Sie Ihr Projekt mit meinem neuen Buch Data Preparation for Machine Learning, das schrittweise Anleitungen und die Python-Quellcodedateien für alle Beispiele enthält.
Lassen Sie uns anfangen.
- Aktualisiert Jun/2020: Die für die Vorhersage verwendete Spalte wurde in den Beispielen geändert.

Statistische Imputation für fehlende Werte im maschinellen Lernen
Foto von Bernal Saborio, einige Rechte vorbehalten.
Übersicht über das Tutorial
Dieses Tutorial ist in drei Teile gegliedert; diese sind:
- Statistische Imputation
- Pferdekolik-Datensatz
- Statistische Imputation mit SimpleImputer
- SimpleImputer Datentransformation
- SimpleImputer und Modellevaluation
- Vergleich verschiedener imputierter Statistiken
- SimpleImputer-Transformation bei der Erstellung einer Vorhersage
Statistische Imputation
Ein Datensatz kann fehlende Werte enthalten.
Dabei handelt es sich um Datenzeilen, in denen ein oder mehrere Werte oder Spalten in dieser Zeile nicht vorhanden sind. Die Werte können vollständig fehlen oder mit einem speziellen Zeichen oder Wert, wie z. B. einem Fragezeichen „?“, gekennzeichnet sein.
Diese Werte können auf viele Arten ausgedrückt werden. Ich habe gesehen, dass sie unter anderem als gar nichts, als leere Zeichenkette, als explizite Zeichenkette NULL oder undefiniert oder N/A oder NaN und als die Zahl 0 angezeigt werden. Unabhängig davon, wie sie in Ihrem Datensatz erscheinen, wird das Wissen, was zu erwarten ist, und die Überprüfung, ob die Daten dieser Erwartung entsprechen, Probleme bei der Verwendung der Daten verringern.
– Seite 10, Bad Data Handbook, 2012.
Werte können aus vielen Gründen fehlen, die oft spezifisch für den Problembereich sind und Gründe wie beschädigte Messungen oder die Nichtverfügbarkeit von Daten umfassen können.
Sie können aus einer Reihe von Gründen auftreten, wie z. B. defekte Messgeräte, Änderungen des Versuchsplans während der Datenerfassung und Zusammenstellung mehrerer ähnlicher, aber nicht identischer Datensätze.
– Seite 63, Data Mining: Practical Machine Learning Tools and Techniques, 2016.
Die meisten Algorithmen für maschinelles Lernen erfordern numerische Eingabewerte und einen Wert für jede Zeile und Spalte in einem Datensatz. Fehlende Werte können daher Probleme für Algorithmen des maschinellen Lernens verursachen.
Es ist daher üblich, fehlende Werte in einem Datensatz zu identifizieren und sie durch einen numerischen Wert zu ersetzen. Dies wird als Datenimputation oder Imputation fehlender Daten bezeichnet.
Ein einfacher und beliebter Ansatz zur Datenimputation beinhaltet die Verwendung statistischer Methoden, um einen Wert für eine Spalte aus den vorhandenen Werten zu schätzen und dann alle fehlenden Werte in der Spalte durch die berechnete Statistik zu ersetzen.
Es ist einfach, weil Statistiken schnell zu berechnen sind, und es ist beliebt, weil es sich oft als sehr effektiv erweist.
Gängige berechnete Statistiken sind:
- Der Spaltenmittelwert.
- Der Spaltenmedianwert.
- Der Spaltenmoduswert.
- Ein konstanter Wert.
Nun, da wir mit statistischen Methoden zur Imputation fehlender Werte vertraut sind, lassen Sie uns einen Blick auf einen Datensatz mit fehlenden Werten werfen.
Möchten Sie mit der Datenvorbereitung beginnen?
Nehmen Sie jetzt an meinem kostenlosen 7-tägigen E-Mail-Crashkurs teil (mit Beispielcode).
Klicken Sie hier, um sich anzumelden und eine kostenlose PDF-Ebook-Version des Kurses zu erhalten.
Laden Sie Ihren KOSTENLOSEN Mini-Kurs herunter
Pferdekolik-Datensatz
Der Pferdekolik-Datensatz beschreibt die medizinischen Merkmale von Pferden mit Koliken und ob sie leben oder sterben.
Es gibt 300 Zeilen und 26 Eingabevariablen mit einer Ausgabevariablen. Es handelt sich um eine binäre Klassifizierungsvorhersageaufgabe, bei der 1 vorhergesagt wird, wenn das Pferd lebt, und 2, wenn das Pferd stirbt.
Es gibt viele Felder, die wir für die Vorhersage in diesem Datensatz auswählen können. In diesem Fall werden wir vorhersagen, ob das Problem chirurgisch war oder nicht (Spaltenindex 23), so dass es sich um ein binäres Klassifizierungsproblem handelt.
Der Datensatz enthält zahlreiche fehlende Werte für viele der Spalten, wobei jeder fehlende Wert mit einem Fragezeichen („?“) markiert ist.
Unten finden Sie ein Beispiel für Zeilen aus dem Datensatz mit markierten fehlenden Werten.
|
1
2
3
4
5
|
2,1,530101,38.50,66,28,3,3,?,2,5,4,4,?,?,?,3,5,45.00,8.40,?,?,2,2,11300,00000,00000,2
1,1,534817,39.2,88,20,?,?,4,1,3,4,2,?,?,?,4,2,50,85,2,2,3,2,02208,00000,00000,2
2,1,530334,38.30,40,24,1,1,3,1,3,3,1,?,?,?,1,1,33.00,6.70,?,?,1,2,00000,00000,00000,1
1,9,5290409,39.10,164,84,4,1,6,2,2,4,4,1,2,5.00,3,?,48.00,7.20,3,5.30,2,1,02208,00000,00000,1
…
|
Sie können hier mehr über den Datensatz erfahren:
- Pferdekolik-Datensatz
- Pferdekolik-Datensatz-Beschreibung
Der Datensatz muss nicht heruntergeladen werden, da wir ihn in den Arbeitsbeispielen automatisch herunterladen.
Fehlende Werte in einem mit Python geladenen Datensatz mit einem NaN-Wert (keine Zahl) zu markieren, ist eine bewährte Praxis.
Wir können den Datensatz mit der Pandas-Funktion read_csv() laden und die Option „na_values“ angeben, um Werte von ‚?‘ als fehlend, markiert mit einem NaN-Wert, zu laden.
|
1
2
3
4
|
…
# load dataset
url = ‚https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv‘
dataframe = read_csv(url, header=None, na_values=‘?‘)
|
Nach dem Laden können wir die geladenen Daten überprüfen, um zu bestätigen, dass „?“ Werte als NaN markiert sind.
|
1
2
3
|
…
# die ersten paar Zeilen zusammenfassen
print(dataframe.head())
|
Wir können dann jede Spalte aufzählen und die Anzahl der Zeilen mit fehlenden Werten für die Spalte melden.
|
1
2
3
4
5
6
7
|
…
# die Anzahl der Zeilen mit fehlenden Werten für jede Spalte zusammenfassen
for i in range(dataframe.shape):
# Anzahl der Zeilen mit fehlenden Werten zählen
n_miss = dataframe].isnull().sum()
perc = n_miss / dataframe.shape * 100
print(‚> %d, Fehlt: %d (%.1f%%)‘ % (i, n_miss, perc))
|
Das vollständige Beispiel für das Laden und Zusammenfassen des Datensatzes ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
# Zusammenfassung des Datensatzes für Pferdekoliken
from pandas import read_csv
# Datensatz laden
url = ‚https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv‘
dataframe = read_csv(url, header=None, na_values=‘?‘)
# die ersten Zeilen zusammenfassen
print(dataframe.head())
# die Anzahl der Zeilen mit fehlenden Werten für jede Spalte zusammenfassen
for i in range(datenrahmen.form):
# Anzahl der Zeilen mit fehlenden Werten zählen
n_miss = dataframe].isnull().sum()
perc = n_miss / dataframe.shape * 100
print(‚> %d, Missing: %d (%.1f%%)‘ % (i, n_miss, perc))
|
Das Ausführen des Beispiels lädt zunächst den Datensatz und fasst die ersten fünf Zeilen zusammen.
Wir können sehen, dass die fehlenden Werte, die mit einem „?“-Zeichen markiert waren, durch NaN-Werte ersetzt wurden.
Als Nächstes sehen wir die Liste aller Spalten im Datensatz und die Anzahl und den Prozentsatz der fehlenden Werte.
Wir können sehen, dass einige Spalten (z. B. Spaltenindex 1 und 2) keine fehlenden Werte haben und andere Spalten (z. B. Spaltenindex 15 und 21) viele oder sogar die Mehrheit der fehlenden Werte haben.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
> 0, Missing: 1 (0.3%)
> 1, Fehlt: 0 (0.0%)
> 2, Fehlt: 0 (0,0%)
> 3, Fehlende: 60 (20,0%)
> 4, Fehlende: 24 (8,0%)
> 5, Fehlende: 58 (19,3%)
> 6, Fehlende: 56 (18,7%)
> 7, Fehlende: 69 (23,0%)
> 8, Fehlende: 47 (15,7%)
> 9, Fehlende: 32 (10,7%)
> 10, Fehlende: 55 (18,3%)
> 11, Fehlende: 44 (14,7%)
> 12, Fehlende: 56 (18,7%)
> 13, Fehlende: 104 (34,7%)
> 14, Fehlende: 106 (35,3%)
> 15, Fehlende: 247 (82,3%)
> 16, Fehlende: 102 (34,0%)
> 17, Fehlende: 118 (39,3%)
> 18, Fehlende: 29 (9,7%)
> 19, Fehlende: 33 (11,0%)
> 20, Fehlende: 165 (55,0%)
> 21, Fehlende: 198 (66,0%)
> 22, Fehlende: 1 (0.3%)
> 23, Fehlende: 0 (0,0%)
> 24, Fehlt: 0 (0,0%)
> 25, Fehlt: 0 (0,0%)
> 26, Fehlt: 0 (0,0%)
> 27, Fehlt: 0 (0.0%)
|
Nun, da wir mit dem Pferdekolik-Datensatz mit fehlenden Werten vertraut sind, schauen wir uns an, wie wir die statistische Imputation verwenden können.
Statistische Imputation mit SimpleImputer
Die scikit-learn-Bibliothek für maschinelles Lernen bietet die Klasse SimpleImputer, die die statistische Imputation unterstützt.
In diesem Abschnitt werden wir untersuchen, wie die SimpleImputer-Klasse effektiv genutzt werden kann.
SimpleImputer Data Transform
Der SimpleImputer ist eine Datentransformation, die zunächst auf der Grundlage der Art der Statistik konfiguriert wird, die für jede Spalte berechnet werden soll, z.z.B. mean.
|
1
2
3
|
…
# define imputer
imputer = SimpleImputer(strategy=’mean‘)
|
Dann wird der Imputer an einen Datensatz angepasst, um die Statistik für jede Spalte zu berechnen.
|
1
2
3
|
…
# fit auf den Datensatz
imputer.fit(X)
|
Der fit imputer wird dann auf einen Datensatz angewendet, um eine Kopie des Datensatzes zu erstellen, bei der alle fehlenden Werte für jede Spalte durch einen statistischen Wert ersetzt werden.
|
1
2
3
|
…
# transformiere den Datensatz
Xtrans = imputer.transform(X)
|
Wir können die Anwendung am Datensatz für Pferdekoliken demonstrieren und bestätigen, dass sie funktioniert, indem wir die Gesamtzahl der fehlenden Werte im Datensatz vor und nach der Transformation zusammenfassen.
Das vollständige Beispiel ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
# statistische Imputation Transformation für den Pferdekolik-Datensatz
from numpy import isnan
from pandas import read_csv
from sklearn.impute import SimpleImputer
# load dataset
url = ‚https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv‘
dataframe = read_csv(url, header=None, na_values=‘?‘)
# split into input and output elements
data = dataframe.values
ix = ) if i != 23]
X, y = data, data
# print total missing
print(‚Missing: %d‘ % sum(isnan(X).flatten()))
# define imputer
imputer = SimpleImputer(strategy=’mean‘)
# fit on the dataset
imputer.fit(X)
# Transformieren des Datensatzes
Xtrans = imputer.transform(X)
# print total missing
print(‚Missing: %d‘ % sum(isnan(Xtrans).flatten()))
|
Das Ausführen des Beispiels lädt zunächst den Datensatz und meldet die Gesamtzahl der fehlenden Werte im Datensatz als 1.605.
Die Transformation wird konfiguriert, angepasst und ausgeführt, und der resultierende neue Datensatz weist keine fehlenden Werte auf, was bestätigt, dass sie wie erwartet ausgeführt wurde.
Jeder fehlende Wert wurde durch den Mittelwert der entsprechenden Spalte ersetzt.
|
1
2
|
Fehlt: 1605
Fehlt: 0
|
EinfacheRechner- und Modellevaluation
Es ist eine gute Praxis, Modelle des maschinellen Lernens auf einem Datensatz mit k-facher Kreuzvalidierung zu evaluieren.
Um die statistische Imputation fehlender Daten korrekt anzuwenden und Datenlecks zu vermeiden, ist es erforderlich, dass die für jede Spalte berechneten Statistiken nur auf dem Trainingsdatensatz berechnet werden und dann auf die Trainings- und Testsätze für jeden Fold im Datensatz angewendet werden.
Wenn wir Resampling verwenden, um Tuning-Parameterwerte auszuwählen oder die Leistung zu schätzen, sollte die Imputation in das Resampling integriert werden.
– Seite 42, Applied Predictive Modeling, 2013.
Dies kann durch die Erstellung einer Modellierungspipeline erreicht werden, bei der der erste Schritt die statistische Imputation ist und der zweite Schritt dann das Modell ist. Dies kann mit der Klasse Pipeline erreicht werden.
Die nachstehende Pipeline verwendet zum Beispiel einen SimpleImputer mit einer „Mittelwert“-Strategie, gefolgt von einem Random-Forest-Modell.
|
1
2
3
4
5
|
…
# define modeling pipeline
model = RandomForestClassifier()
imputer = SimpleImputer(strategy=’mean‘)
pipeline = Pipeline(steps=)
|
Wir können den mean-imputierten Datensatz und die Random-Forest-Modellierungspipeline für den Pferdekolik-Datensatz mit wiederholter 10-facher Kreuzvalidierung bewerten.
Das vollständige Beispiel ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
# Mittelwert-Imputation und Random Forest für forest für den Pferdekolik-Datensatz
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
# load dataset
url = ‚https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv‘
dataframe = read_csv(url, header=None, na_values=‘?‘)
# split into input and output elements
data = dataframe.values
ix = ) if i != 23]
X, y = Daten, data
# define modeling pipeline
model = RandomForestClassifier()
imputer = SimpleImputer(strategy=’mean‘)
pipeline = Pipeline(steps=)
# define model evaluation
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
# Modell auswerten
scores = cross_val_score(pipeline, X, y, scoring=’accuracy‘, cv=cv, n_jobs=-1)
print(‚Mean Accuracy: %.3f (%.3f)‘ % (mean(scores), std(scores)))
|
Die korrekte Ausführung des Beispiels wendet die Datenimputation auf jeden Fold des Kreuzvalidierungsverfahrens an.
Hinweis: Ihre Ergebnisse können aufgrund der stochastischen Natur des Algorithmus oder des Bewertungsverfahrens oder aufgrund von Unterschieden in der numerischen Präzision variieren. Führen Sie das Beispiel einige Male aus und vergleichen Sie das durchschnittliche Ergebnis.
Die Pipeline wird mit drei Wiederholungen der 10-fachen Kreuzvalidierung evaluiert und meldet eine mittlere Klassifizierungsgenauigkeit für den Datensatz von etwa 86.3 Prozent, was ein guter Wert ist.
|
1
|
Mittlere Genauigkeit: 0.863 (0.054)
|
Vergleich verschiedener imputierter Statistiken
Woher wissen wir, dass die Verwendung einer „mittleren“ statistischen Strategie gut oder am besten für diesen Datensatz ist?
Die Antwort ist, dass wir es nicht wissen und dass sie willkürlich gewählt wurde.
Wir können ein Experiment entwerfen, um jede statistische Strategie zu testen und herauszufinden, welche für diesen Datensatz am besten funktioniert, indem wir die Strategien Mittelwert, Median, Modus (am häufigsten) und Konstant (0) vergleichen. Die durchschnittliche Genauigkeit jedes Ansatzes kann dann verglichen werden.
Das vollständige Beispiel ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
# vergleichen Statistische Imputationsstrategien für den Pferdekolik-Datensatz
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.pipeline import Pipeline
from matplotlib import pyplot
# load dataset
url = ‚https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv‘
dataframe = read_csv(url, header=None, na_values=‘?‘)
# split into input and output elements
data = dataframe.values
ix = ) if i != 23]
X, y = data, data
# jede Strategie auf dem Datensatz auswerten
results = list()
strategies =
for s in strategies:
# die Modellierungspipeline erstellen
pipeline = Pipeline(steps=)
# das Modell auswerten
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores = cross_val_score(pipeline, X, y, scoring=’accuracy‘, cv=cv, n_jobs=-1)
# Ergebnisse speichern
results.append(scores)
print(‚>%s %.3f (%.3f)‘ % (s, mean(scores), std(scores)))
# Plotten der Modellleistung zum Vergleich
pyplot.boxplot(results, labels=strategies, showmeans=True)
pyplot.show()
|
Das Ausführen des Beispiels evaluiert jede statistische Imputationsstrategie auf dem Pferdekolik-Datensatz mit wiederholter Kreuzvalidierung.
Hinweis: Ihre Ergebnisse können aufgrund der stochastischen Natur des Algorithmus oder des Bewertungsverfahrens oder aufgrund von Unterschieden in der numerischen Präzision variieren. Führen Sie das Beispiel einige Male durch und vergleichen Sie das durchschnittliche Ergebnis.
Die mittlere Genauigkeit jeder Strategie wird im Verlauf angegeben. Die Ergebnisse deuten darauf hin, dass die Verwendung eines konstanten Wertes, z. B. 0, die beste Leistung von etwa 88,1 Prozent ergibt, was ein hervorragendes Ergebnis ist.
|
1
2
3
4
|
> Mittelwert 0.860 (0.054)
>Mittelwert 0.862 (0.065)
>häufigste 0,872 (0,052)
>Konstante 0,881 (0,047)
|
Am Ende des Durchlaufs wird für jeden Ergebnissatz ein Box- und Whisker-Plot erstellt, mit dem die Verteilung der Ergebnisse verglichen werden kann.
Es ist deutlich zu erkennen, dass die Verteilung der Genauigkeitsergebnisse für die konstante Strategie besser ist als die der anderen Strategien.
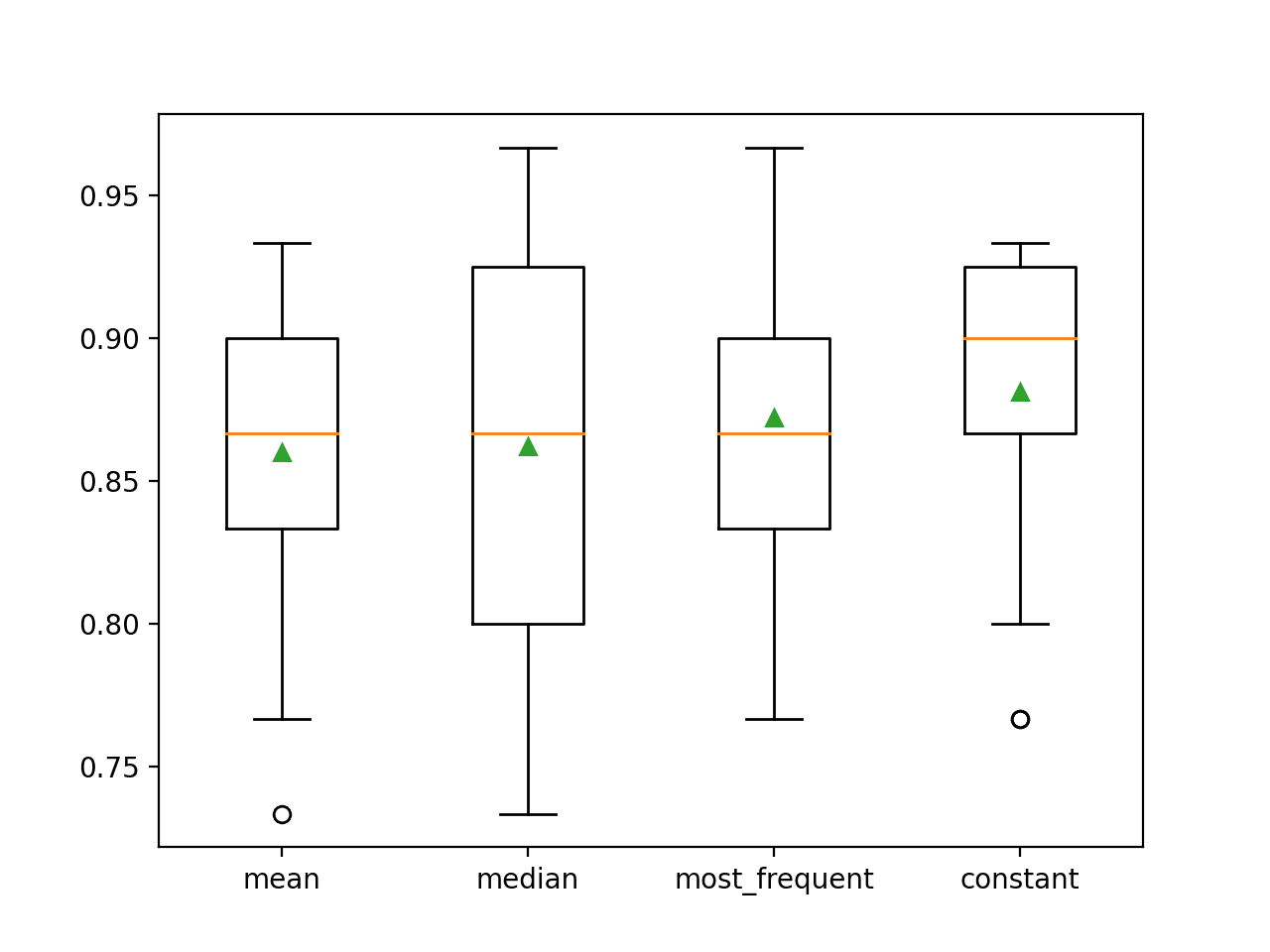
Box and Whisker Plot of Statistical Imputation Strategies Applied to the Horse Colic Dataset
SimpleImputer Transform When Making a Prediction
Wir möchten vielleicht eine endgültige Modellierungspipeline mit der konstanten Imputationsstrategie und dem Random-Forest-Algorithmus erstellen und dann eine Vorhersage für neue Daten treffen.
Dies kann erreicht werden, indem man die Pipeline definiert und sie an alle verfügbaren Daten anpasst und dann die Funktion predict() aufruft, wobei neue Daten als Argument angegeben werden.
Wichtig ist, dass die Zeile mit den neuen Daten alle fehlenden Werte mit dem Wert NaN markiert.
|
1
2
3
|
…
# define new data
row =
|
Das vollständige Beispiel ist unten aufgeführt.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# konstante Imputation Strategie und Vorhersage für den Schlauchkolik-Datensatz
from numpy import nan
from pandas import read_csv
from sklearn.ensemble import RandomForestClassifier
from sklearn.impute import SimpleImputer
from sklearn.pipeline import Pipeline
# load dataset
url = ‚https://raw.githubusercontent.com/jbrownlee/Datasets/master/horse-colic.csv‘
dataframe = read_csv(url, header=None, na_values=‘?‘)
# split into input and output elements
data = dataframe.values
ix = ) if i != 23]
X, y = Daten, Daten
# Erstellen der Modellierungspipeline
Pipeline = Pipeline(steps=)
# Anpassen des Modells
Pipeline.fit(X, y)
# neue Daten definieren
row =
# eine Vorhersage machen
yhat = pipeline.predict()
# Vorhersage zusammenfassen
print(‚Predicted Class: %d‘ % yhat)
|
Das Ausführen des Beispiels passt die Modellierungspipeline auf alle verfügbaren Daten an.
Eine neue Datenreihe wird definiert, wobei fehlende Werte mit NaNs markiert werden, und eine Klassifizierungsvorhersage wird erstellt.
|
1
|
Vorhersageklasse: 2
|
Weitere Lektüre
In diesem Abschnitt finden Sie weitere Ressourcen zu diesem Thema, wenn Sie das Thema vertiefen möchten.
Verwandte Tutorials
- Ergebnisse für Standard-Klassifikations- und Regressionsdatensätze des maschinellen Lernens
- How to Handle Missing Data with Python
Bücher
- Bad Data Handbook, 2012.
- Data Mining: Practical Machine Learning Tools and Techniques, 2016.
- Applied Predictive Modeling, 2013.
APIs
- Imputation of missing values, scikit-learn Documentation.
- sklearn.impute.SimpleImputer API.
Datensatz
- Pferdekolik-Datensatz
- Pferdekolik-Datensatzbeschreibung
Zusammenfassung
In diesem Tutorial haben Sie entdeckt, wie man statistische Imputationsstrategien für fehlende Daten im maschinellen Lernen verwendet.
Speziell haben Sie gelernt:
- Fehlende Werte müssen mit NaN-Werten markiert werden und können durch statistische Maße ersetzt werden, um die Wertespalte zu berechnen.
- Wie man einen CSV-Wert mit fehlenden Werten lädt und die fehlenden Werte mit NaN-Werten markiert und die Anzahl und den Prozentsatz der fehlenden Werte für jede Spalte berichtet.
- Wie man fehlende Werte mit Hilfe von Statistiken als Datenaufbereitungsmethode bei der Bewertung von Modellen und bei der Anpassung eines endgültigen Modells zur Erstellung von Vorhersagen für neue Daten unterstellt.
Haben Sie Fragen?
Stellen Sie Ihre Fragen in den Kommentaren unten und ich werde mein Bestes tun, um sie zu beantworten.
Get a Handle on Modern Data Preparation!

Prepare Your Machine Learning Data in Minutes
…mit nur ein paar Zeilen Python-Code
Entdecken Sie in meinem neuen Ebook:
Datenaufbereitung für maschinelles Lernen
Es bietet Tutorials zum Selbststudium mit vollständigem Arbeitscode zu:
Feature Selection, RFE, Data Cleaning, Data Transforms, Scaling, Dimensionality Reduction, und vielem mehr….
Bringen Sie moderne Datenaufbereitungstechniken in
Ihre Machine Learning Projekte
Sehen Sie, was drin ist