Punktsymmetrie liegt vor, wenn die Figur um einen einzigen Punkt herum gezeichnet wird.

Dieser Punkt wird Mittelpunkt der Figur oder Mittelpunkt der Symmetrie genannt. In der nebenstehenden Abbildung sehen wir, dass dem Punkt X auf der Figur ein Punkt X‘ auf der anderen Seite des Mittelpunkts entspricht, der X direkt gegenüberliegt und auf der Figur liegt. Wir sagen, dass die Figur um den Mittelpunkt symmetrisch ist.
Anmerkung:
Wenn wir eine Figur um 180° drehen und sie ihre ursprüngliche Form wiedererhält, dann sagen wir, dass die Figur punktsymmetrisch ist.
Beispiele für Figuren, die Punktsymmetrie aufweisen:
● Alle Buchstaben des englischen Alphabets.
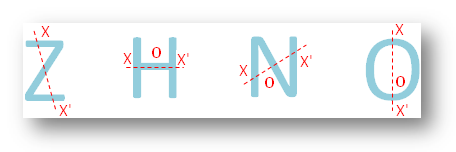
● Verschiedene geometrische Figuren.
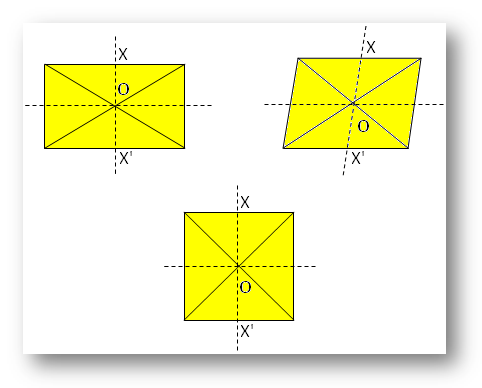
Anmerkung:
Hier ist O der Mittelpunkt der Symmetrie.
Bezüglich X gibt es X‘, so dass X‘ auf der anderen Seite von O direkt gegenüber von X liegt.
Welche Bedingungen erfüllt eine Form oder eine Figur für die Punktsymmetrie?
Die Bedingungen, die eine Form oder eine Figur für die Punktsymmetrie erfüllt, d.h. jedes Teil sollte ein passendes Teil haben
– der Abstand sollte vom Mittelpunkt gleich sein
– aber in entgegengesetzter Richtung.
● Verwandte Konzepte
● Lineare Symmetrie
● Symmetrielinien
● Rotationssymmetrie
● Ordnung der Rotationssymmetrie
● Arten der Symmetrie
● Reflexion
● Reflexion eines Punktes an der x-Achse
● Spiegelung eines Punktes an der y-.Achse
● Reflexion eines Punktes am Ursprung
● Drehung
● Drehung um 90 Grad im Uhrzeigersinn
● Drehung um 90 Grad gegen den Uhrzeigersinn
● Drehung um 180 Grad
7. Klasse Mathe-Probleme
8. Klasse Mathe-Übungen
Von der Punktsymmetrie zur HOME PAGE