Pearson Mode Skewness

Statistik Definitionen > Pearson Mode Skewness

Die Pearson Mode Skewness, auch Pearson’s first coefficient of skewness genannt, ist eine Möglichkeit, die Schiefe einer Verteilung zu ermitteln.

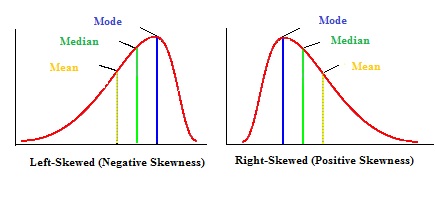
Mittelwert, Modus und Median können verwendet werden, um herauszufinden, ob man eine positiv oder negativ schiefe Verteilung hat.

• Ist der Mittelwert größer als der Modus, ist die Verteilung positiv schief.
• Ist der Mittelwert kleiner als der Modus, ist die Verteilung negativ schief.
• Ist der Mittelwert größer als der Median, so ist die Verteilung positiv schief.
• Ist der Mittelwert kleiner als der Median, so ist die Verteilung negativ schief.

Pearson Modus Schiefe

Der Modus Schiefe verwendet die oben genannten Fakten, um herauszufinden, ob eine positive oder negative Schiefe vorliegt. Wenn Sie eine Verteilung haben und den Mittelwert, den Modus und die Standardabweichung (σ) kennen, dann lautet die Formel für die Pearsonsche Modus-Schiefe:

(Mittelwert-Modus)/σ

Problemstellung: Sie haben Daten mit einem Mittelwert von 19, einem Modus von 20 und einer Standardabweichung von 25. Was sagt die Pearson-Mode-Schiefe über die Verteilung aus?
(Mittelwert-Mode)/σ = (19-20)/25 = -0,04.
Es besteht eine sehr geringe negative Schiefe (-0,04). Hinweis: Für die meisten Zwecke würde dies als symmetrische Verteilung gelten, da die Schiefe so gering ist.

Pearson Mode Skewness: Alternative Formel.

Wenn Sie den Modus nicht kennen, können Sie die Pearson-Modus-Schiefe nicht verwenden. Die Richtung der Schiefe lässt sich jedoch auch ermitteln, indem man herausfindet, wo der Mittelwert und der Median liegen. Nach der Wirtschaftsstatistik führt dies zu einer zweiten, gleichwertigen Formel:

3(Mittelwert – Median) / σ

Diese Formel wird auch als zweiter Schiefekoeffizient von Pearson bezeichnet.

Pearson Modus Schiefe: Was die Ergebnisse bedeuten.

Die Differenz zwischen Mittelwert und Modus bzw. Mittelwert und Median gibt an, wie weit die Verteilung von der Symmetrie abweicht. Eine symmetrische Verteilung (z. B. die Normalverteilung) hat eine Schiefe von Null.
Beide Gleichungen geben die Ergebnisse in Standardabweichungen an, die dimensionslose Maßeinheiten vom Mittelwert sind.

Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder einer Prüfungsfrage? Mit Chegg Study können Sie Schritt-für-Schritt-Lösungen für Ihre Fragen von einem Experten auf dem Gebiet erhalten. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!