Matrixalgebra

Wir werden drei Beispiele aus den Biowissenschaften beschreiben: eines aus der Physik, eines aus der Genetik und eines aus einem Mäuseversuch. Sie sind sehr unterschiedlich, und doch verwenden wir am Ende die gleiche statistische Technik: die Anpassung linearer Modelle. Lineare Modelle werden normalerweise in der Sprache der Matrixalgebra gelehrt und beschrieben.

Motivierende Beispiele

Fallende Objekte

Stellen Sie sich vor, Sie sind Galileo im 16. Jahrhundert und versuchen, die Geschwindigkeit eines fallenden Objekts zu beschreiben. Ein Assistent klettert auf den Turm von Pisa und lässt eine Kugel fallen, während mehrere andere Assistenten die Position zu verschiedenen Zeiten aufzeichnen. Simulieren wir einige Daten unter Verwendung der Gleichungen, die wir heute kennen, und fügen wir einen Messfehler hinzu:

set.seed(1)g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, note: we use tt because t is a base functiond <- 56.67 - 0.5*g*tt^2 + rnorm(n,sd=1) ##meters

Die Assistenten geben die Daten an Galileo weiter, und das ist, was er sieht:

mypar()plot(tt,d,ylab="Distance in meters",xlab="Time in seconds")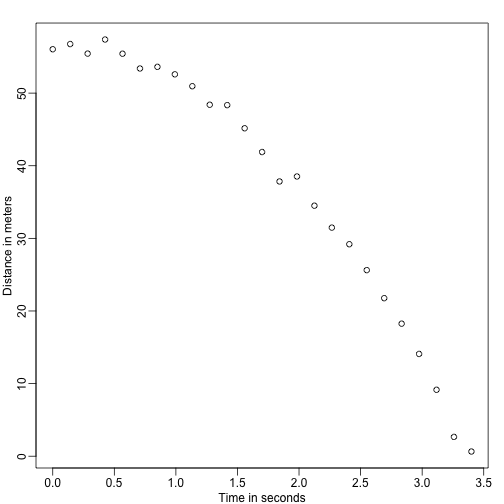

Er kennt die genaue Gleichung nicht, aber aus der obigen Darstellung schließt er, dass die Position einer Parabel folgen sollte. Also modelliert er die Daten mit:

Mit, das für den Ort steht, die Zeit darstellt und den Messfehler berücksichtigt. Dies ist ein lineares Modell, weil es eine lineare Kombination aus bekannten Größen (th s), die als Prädiktoren oder Kovariaten bezeichnet werden, und unbekannten Parametern (die s) ist.

Vater &Sohn-Höhen

Stellen Sie sich nun vor, Sie sind Francis Galton im 19. Jahrhundert und Sie sammeln paarweise Höhendaten von Vätern und Söhnen. Sie vermuten, dass die Körpergröße vererbt wird. Ihre Daten:

library(UsingR)x=father.son$fheighty=father.son$sheight

sehen so aus:

plot(x,y,xlab="Father's height",ylab="Son's height")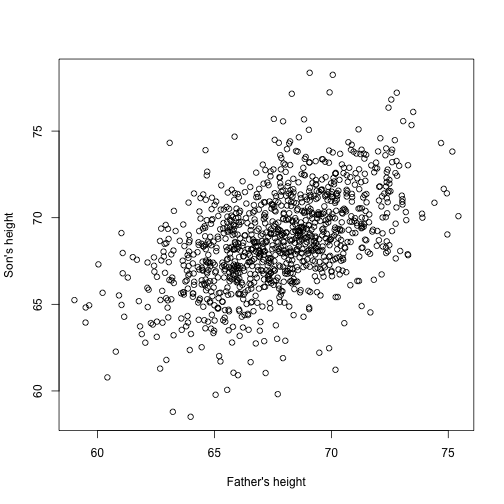

Die Körpergröße der Söhne scheint linear mit der Körpergröße der Väter zuzunehmen. In diesem Fall sieht ein Modell, das die Daten beschreibt, wie folgt aus:

Dies ist ebenfalls ein lineares Modell mit und , der Höhe des Vaters bzw. des Sohnes, für das -te Paar und einem Term, der die zusätzliche Variabilität berücksichtigt. In diesem Fall betrachten wir die Größe des Vaters als Prädiktor und als feststehend (nicht zufällig), weshalb wir Kleinbuchstaben verwenden. Messfehler allein können nicht die gesamte Variabilität erklären, die in . Dies ist sinnvoll, da es andere Variablen gibt, die nicht im Modell enthalten sind, z. B. die Größe der Mütter, genetische Zufälligkeiten und Umweltfaktoren.

Stichproben aus mehreren Populationen

Hier lesen wir Daten zum Körpergewicht von Mäusen ein, die mit zwei verschiedenen Futtermitteln gefüttert wurden: fettreiches Futter und Kontrollfutter (Chow). Wir haben jeweils eine Zufallsstichprobe von 12 Mäusen. Wir wollen herausfinden, ob die Ernährung einen Einfluss auf das Gewicht hat. Hier sind die Daten:

dat <- read.csv("femaleMiceWeights.csv")mypar(1,1)stripchart(Bodyweight~Diet,data=dat,vertical=TRUE,method="jitter",pch=1,main="Mice weights")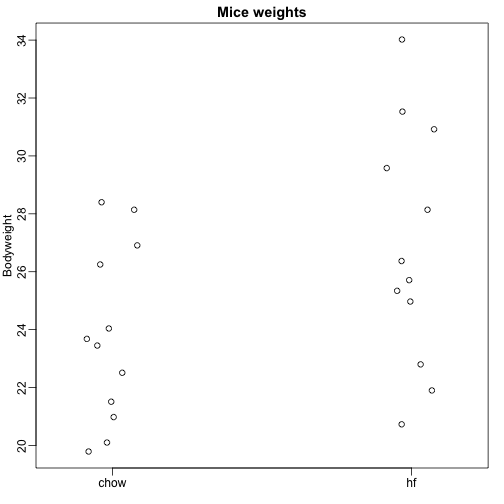

Wir möchten den Unterschied im Durchschnittsgewicht zwischen den Populationen schätzen. Wir haben gezeigt, wie dies mit Hilfe von t-Tests und Konfidenzintervallen auf der Grundlage der Differenz der Stichprobenmittelwerte möglich ist. Wir können genau dieselben Ergebnisse mit einem linearen Modell erhalten:

mit dem Durchschnittsgewicht der Chow-Diät, der Differenz zwischen den Durchschnittswerten, wenn die Maus die fettreiche (hf) Diät erhält, wenn sie die Chow-Diät erhält, und die Unterschiede zwischen Mäusen derselben Population erklärt.

Lineare Modelle im Allgemeinen

Wir haben drei sehr unterschiedliche Beispiele gesehen, in denen lineare Modelle verwendet werden können. Ein allgemeines Modell, das alle oben genannten Beispiele umfasst, ist das folgende:

Beachten Sie, dass wir eine allgemeine Anzahl von Prädiktoren haben. Die Matrixalgebra bietet eine kompakte Sprache und einen mathematischen Rahmen für die Berechnung und Ableitung beliebiger linearer Modelle, die in den obigen Rahmen passen.

Parameter schätzen

Damit die obigen Modelle nützlich sind, müssen wir die unbekannten s schätzen. Im ersten Beispiel wollen wir einen physikalischen Prozess beschreiben, für den wir keine unbekannten Parameter haben können. Im zweiten Beispiel geht es darum, die Vererbung besser zu verstehen, indem man schätzt, wie stark die Größe des Vaters im Durchschnitt die Größe des Sohnes beeinflusst. Im letzten Beispiel wollen wir feststellen, ob es tatsächlich einen Unterschied gibt: wenn .

Der Standardansatz in der Wissenschaft besteht darin, die Werte zu finden, die den Abstand des angepassten Modells zu den Daten minimieren. Die folgende Gleichung wird als kleinste Quadrate (LS) bezeichnet und wir werden sie in diesem Kapitel oft sehen:

Wenn wir das Minimum gefunden haben, nennen wir die Werte die kleinsten quadratischen Schätzungen (LSE) und bezeichnen sie mit . Die Größe, die man erhält, wenn man die Gleichung der kleinsten Quadrate an den Schätzungen auswertet, wird als Residualsumme der Quadrate (RSS) bezeichnet. Da alle diese Größen von abhängen, sind sie Zufallsvariablen. Die s sind Zufallsvariablen, und wir werden schließlich eine Inferenz auf sie durchführen.

Fallendes Objekt – ein neues Beispiel

Dank meines Physiklehrers in der High School weiß ich, dass die Gleichung für die Flugbahn eines fallenden Objekts lautet:

mit und die Ausgangshöhe bzw. Geschwindigkeit. Die Daten, die wir oben simuliert haben, folgten dieser Gleichung und fügten Messfehler hinzu, um n Beobachtungen für das Fallenlassen der Kugel vom Turm von Pisa zu simulieren. Deshalb haben wir diesen Code verwendet, um die Daten zu simulieren:

g <- 9.8 ##meters per secondn <- 25tt <- seq(0,3.4,len=n) ##time in secs, t is a base functionf <- 56.67 - 0.5*g*tt^2y <- f + rnorm(n,sd=1)

So sehen die Daten aus, wobei die durchgezogene Linie die wahre Flugbahn darstellt:

plot(tt,y,ylab="Distance in meters",xlab="Time in seconds")lines(tt,f,col=2)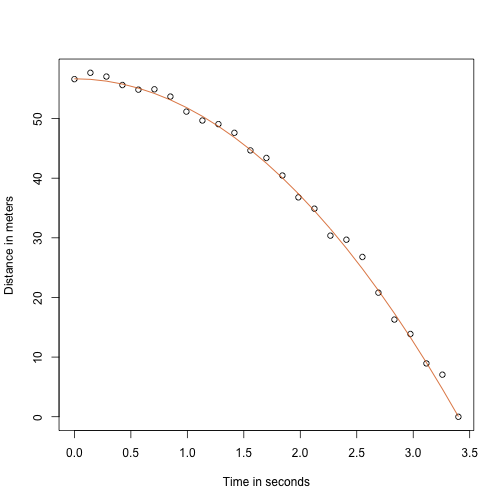

Aber wir haben so getan, als wären wir Galilei und kennen daher die Parameter des Modells nicht. Die Daten deuten darauf hin, dass es sich um eine Parabel handelt, also modellieren wir sie als solche:

Wie finden wir die LSE?

Die lm-Funktion

In R können wir dieses Modell einfach mit der lm-Funktion anpassen. Wir werden diese Funktion später im Detail beschreiben, aber hier ist eine Vorschau:

tt2 <-tt^2fit <- lm(y~tt+tt2)summary(fit)$coef

## Estimate Std. Error t value Pr(>|t|)## (Intercept) 57.1047803 0.4996845 114.281666 5.119823e-32## tt -0.4460393 0.6806757 -0.655289 5.190757e-01## tt2 -4.7471698 0.1933701 -24.549662 1.767229e-17

Sie liefert uns die LSE, sowie Standardfehler und p-Werte.

Teil dessen, was wir in diesem Abschnitt tun, ist es, die Mathematik hinter dieser Funktion zu erklären.

Die Schätzung der kleinsten Quadrate (LSE)

Lassen Sie uns eine Funktion schreiben, die die RSS für jeden Vektor berechnet:

rss <- function(Beta0,Beta1,Beta2){ r <- y - (Beta0+Beta1*tt+Beta2*tt^2) return(sum(r^2))}

So erhalten wir für jeden dreidimensionalen Vektor eine RSS. Hier ist ein Diagramm der RSS in Abhängigkeit davon, ob wir die anderen beiden festhalten:

Beta2s<- seq(-10,0,len=100)plot(Beta2s,sapply(Beta2s,rss,Beta0=55,Beta1=0), ylab="RSS",xlab="Beta2",type="l")##Let's add another curve fixing another pair:Beta2s<- seq(-10,0,len=100)lines(Beta2s,sapply(Beta2s,rss,Beta0=65,Beta1=0),col=2)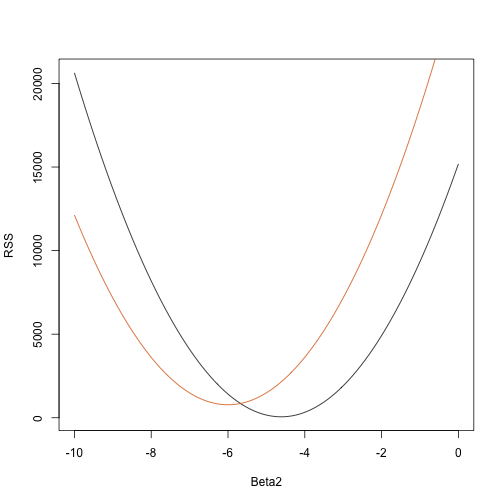

Versuch und Irrtum wird hier nicht funktionieren. Stattdessen können wir die Infinitesimalrechnung anwenden: Wir nehmen die partiellen Ableitungen, setzen sie auf 0 und lösen. Wenn wir viele Parameter haben, können diese Gleichungen natürlich ziemlich komplex werden. Die lineare Algebra bietet eine kompakte und allgemeine Möglichkeit, dieses Problem zu lösen.

Mehr zu Galton (Fortgeschrittene)

Bei der Untersuchung der Vater-Sohn-Daten machte Galton eine faszinierende Entdeckung, indem er eine explorative Analyse durchführte.

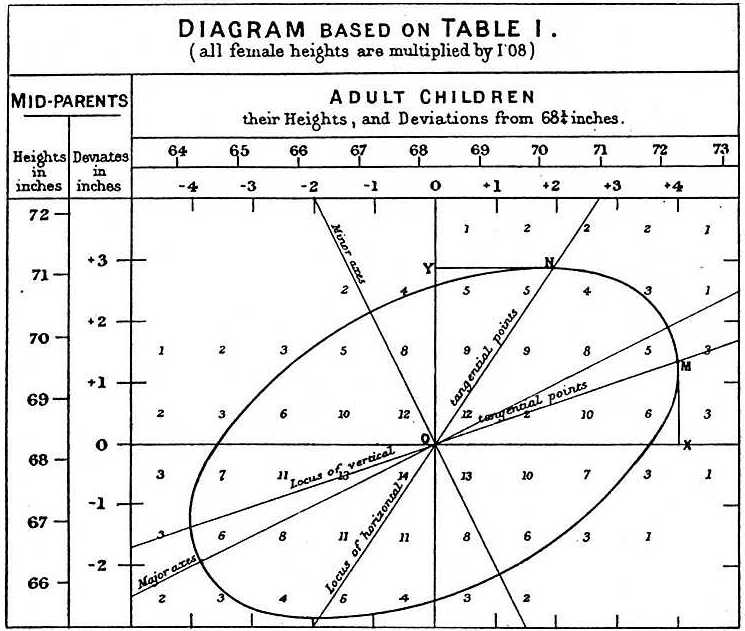
Er stellte fest, dass, wenn er die Anzahl der Vater-Sohn-Höhenpaare tabellarisch darstellte und alle x,y-Werte mit den gleichen Summen in der Tabelle verfolgte, sie eine Ellipse bildeten. In der von Galton erstellten Grafik oben sehen Sie die Ellipse, die durch die Paare mit 3 Fällen gebildet wird. Dies führte dann zur Modellierung dieser Daten als korrelierte bivariate Normalverteilung, die wir bereits beschrieben haben:

Wir haben beschrieben, wie wir mit Hilfe von Mathematik zeigen können, dass, wenn man die Bedingung festhält, die Verteilung von normalverteilt ist mit Mittelwert: und Standardabweichung . Beachten Sie, dass die Korrelation zwischen und ist, was bedeutet, dass, wenn wir fixieren, folgt in der Tat ein lineares Modell. Die Parameter und in unserem einfachen linearen Modell können in Form von , und ausgedrückt werden.