Gepostet am 27. August 2015
Rekurrente neuronale Netze
Menschen fangen nicht jede Sekunde mit dem Denken von vorne an. Wenn du diesen Aufsatz liest, verstehst du jedes Wort auf der Grundlage deines Verständnisses der vorherigen Wörter. Sie werfen nicht alles weg und fangen wieder von vorne an zu denken. Ihre Gedanken sind beständig.
Traditionelle neuronale Netze können das nicht, und das scheint ein großes Manko zu sein. Stellen Sie sich zum Beispiel vor, Sie möchten klassifizieren, welche Art von Ereignis an jedem Punkt eines Films stattfindet. Es ist unklar, wie ein herkömmliches neuronales Netz seine Erkenntnisse über frühere Ereignisse im Film nutzen könnte, um spätere Ereignisse zu informieren.
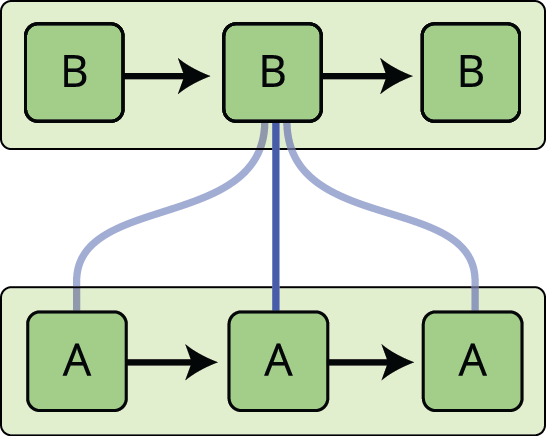
Rekurrente neuronale Netze gehen dieses Problem an. Es handelt sich um Netzwerke mit Schleifen, die es ermöglichen, dass Informationen bestehen bleiben.

Im obigen Diagramm betrachtet ein Teil des neuronalen Netzes, \(A\), eine Eingabe \(x_t\) und gibt einen Wert \(h_t\) aus. Eine Schleife ermöglicht die Weitergabe von Informationen von einem Schritt des Netzes zum nächsten.
Durch diese Schleifen erscheinen rekurrente neuronale Netze etwas mysteriös. Wenn man jedoch etwas mehr nachdenkt, stellt sich heraus, dass sie sich gar nicht so sehr von einem normalen neuronalen Netz unterscheiden. Ein rekurrentes neuronales Netz kann man sich als mehrere Kopien desselben Netzes vorstellen, die jeweils eine Nachricht an einen Nachfolger weitergeben. Betrachten wir, was passiert, wenn wir die Schleife abrollen:
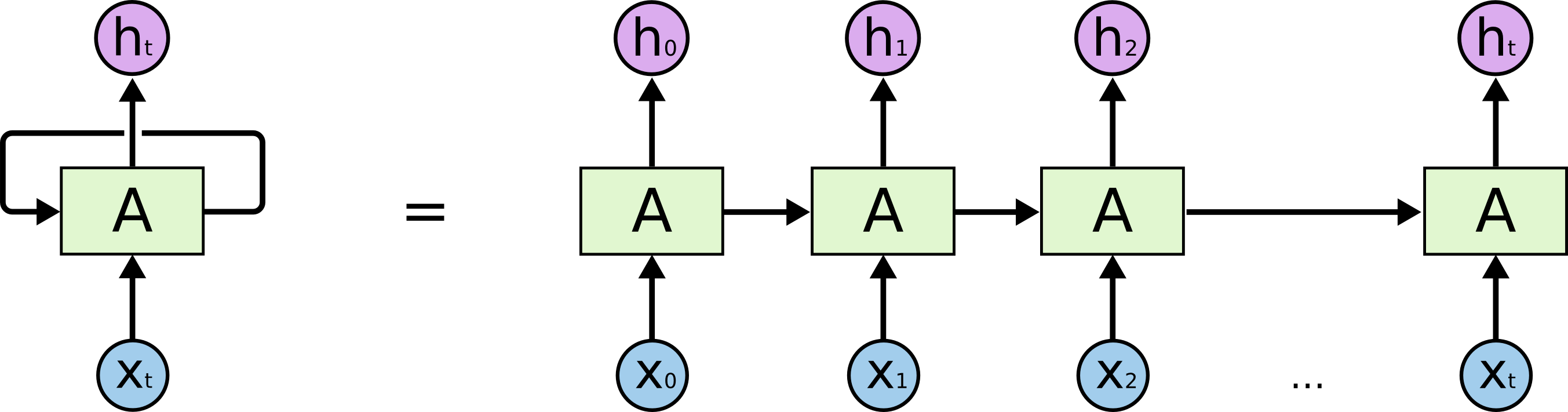
Dieser kettenartige Charakter zeigt, dass rekurrente neuronale Netze eng mit Sequenzen und Listen verwandt sind. Sie sind die natürliche Architektur eines neuronalen Netzes für solche Daten.
Und sie werden auch verwendet! In den letzten Jahren gab es unglaubliche Erfolge bei der Anwendung von RNNs auf eine Vielzahl von Problemen: Spracherkennung, Sprachmodellierung, Übersetzung, Bildbeschriftung… Die Liste geht weiter. Die Diskussion über die erstaunlichen Leistungen, die man mit RNNs erzielen kann, überlasse ich Andrej Karpathys ausgezeichnetem Blogbeitrag The Unreasonable Effectiveness of Recurrent Neural Networks. Aber sie sind wirklich ziemlich erstaunlich.
Wesentlich für diese Erfolge ist die Verwendung von „LSTMs“, einer ganz besonderen Art von rekurrenten neuronalen Netzen, die bei vielen Aufgaben viel besser funktionieren als die Standardversion. Fast alle aufregenden Ergebnisse, die auf rekurrenten neuronalen Netzen basieren, werden mit ihnen erzielt. Es sind diese LSTMs, die in diesem Aufsatz untersucht werden.
Das Problem der langfristigen Abhängigkeiten
Einer der Reize von RNNs ist die Vorstellung, dass sie in der Lage sein könnten, frühere Informationen mit der aktuellen Aufgabe zu verbinden, so wie die Verwendung früherer Videobilder das Verständnis des aktuellen Bildes beeinflussen könnte. Wenn RNNs dies könnten, wären sie äußerst nützlich. Aber können sie das? Das kommt darauf an.
Manchmal müssen wir nur aktuelle Informationen heranziehen, um die aktuelle Aufgabe zu erfüllen. Nehmen wir zum Beispiel ein Sprachmodell, das versucht, das nächste Wort auf der Grundlage der vorangegangenen Wörter vorherzusagen. Wenn wir versuchen, das letzte Wort in „die Wolken sind am Himmel“ vorherzusagen, brauchen wir keinen weiteren Kontext – es ist ziemlich offensichtlich, dass das nächste Wort Himmel sein wird. In solchen Fällen, in denen die Lücke zwischen der relevanten Information und der Stelle, an der sie benötigt wird, klein ist, können RNNs lernen, die vergangene Information zu verwenden.
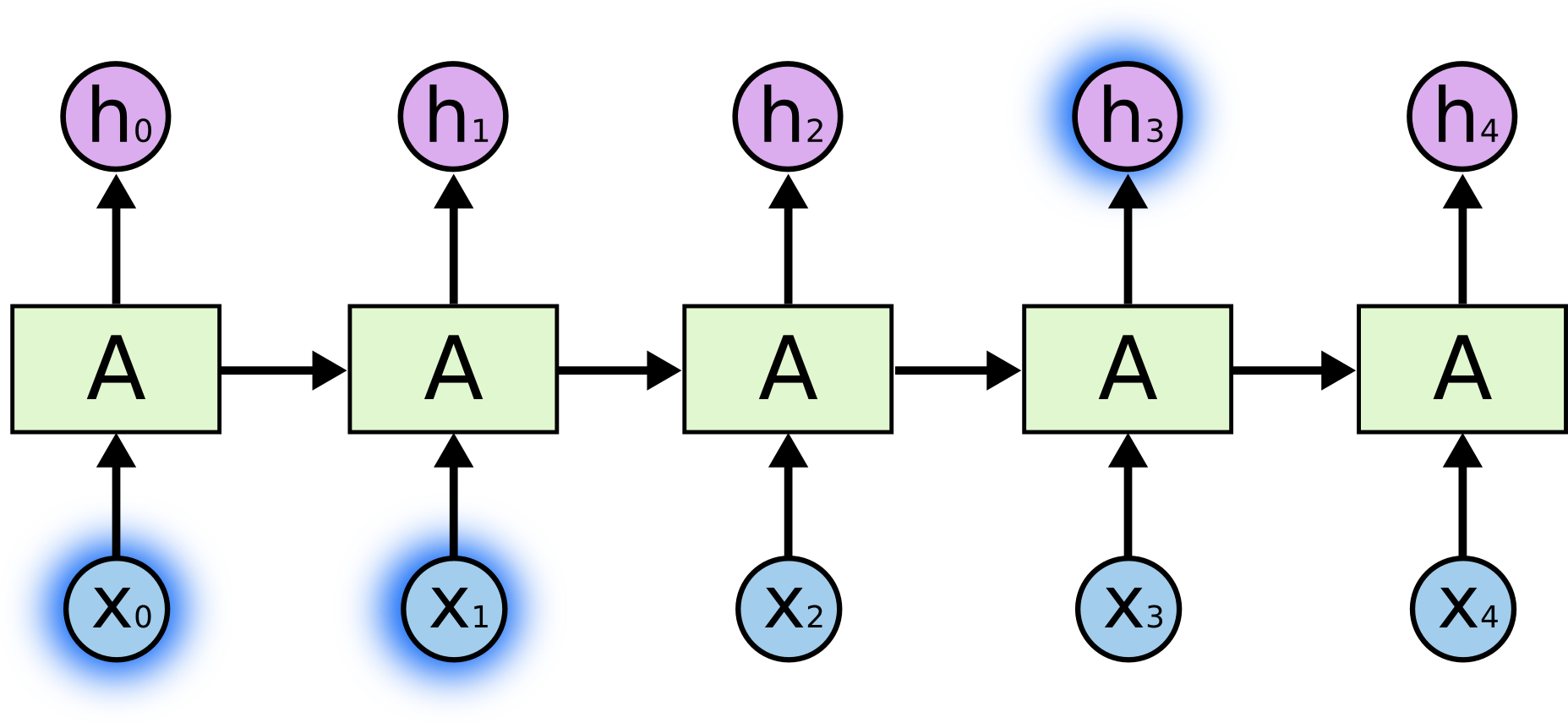
Aber es gibt auch Fälle, in denen wir mehr Kontext benötigen. Nehmen wir an, wir versuchen, das letzte Wort im Text „Ich bin in Frankreich aufgewachsen… Ich spreche fließend Französisch.“ vorherzusagen. Jüngste Informationen deuten darauf hin, dass das nächste Wort wahrscheinlich der Name einer Sprache ist, aber wenn wir eingrenzen wollen, um welche Sprache es sich handelt, brauchen wir den Kontext von Frankreich, der weiter zurückliegt. Es ist durchaus möglich, dass die Lücke zwischen den relevanten Informationen und dem Punkt, an dem sie benötigt werden, sehr groß wird.
Unglücklicherweise sind RNNs mit zunehmender Lücke nicht mehr in der Lage, zu lernen, die Informationen zu verknüpfen.
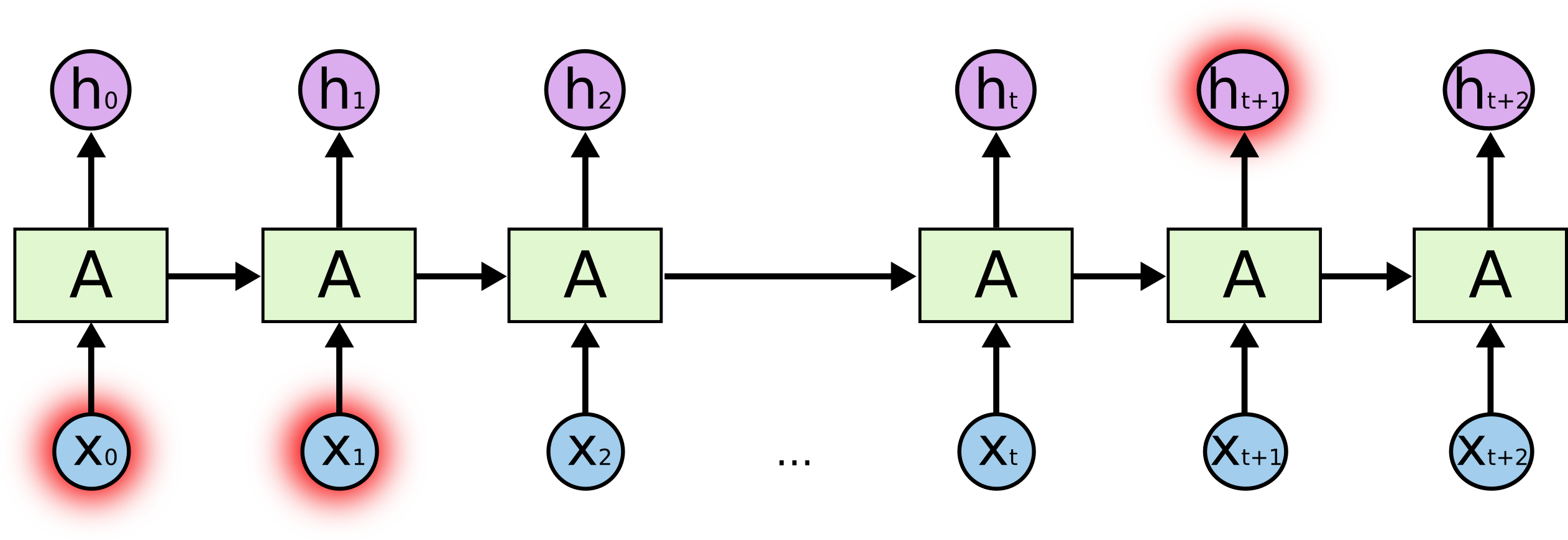
In der Theorie sind RNNs durchaus in der Lage, solche „langfristigen Abhängigkeiten“ zu verarbeiten. Ein Mensch könnte für sie sorgfältig Parameter auswählen, um Spielzeugprobleme dieser Form zu lösen. Leider scheinen RNNs in der Praxis nicht in der Lage zu sein, sie zu lernen. Das Problem wurde von Hochreiter (1991) und Bengio et al. (1994) eingehend untersucht, die einige ziemlich grundlegende Gründe dafür fanden, warum es schwierig sein könnte.
Glücklicherweise haben LSTMs dieses Problem nicht!
LSTM-Netzwerke
Long Short Term Memory-Netzwerke – gewöhnlich einfach „LSTMs“ genannt – sind eine besondere Art von RNN, die in der Lage sind, langfristige Abhängigkeiten zu lernen. Sie wurden von Hochreiter & Schmidhuber (1997) eingeführt und von vielen Personen in nachfolgenden Arbeiten verfeinert und popularisiert.1 Sie funktionieren hervorragend bei einer Vielzahl von Problemen und werden heute weit verbreitet eingesetzt.
LSTMs sind explizit darauf ausgelegt, das Problem der Langzeitabhängigkeit zu vermeiden. Das Erinnern von Informationen über lange Zeiträume ist praktisch ihr Standardverhalten und nicht etwas, das sie mühsam erlernen müssen!
Alle rekurrenten neuronalen Netze haben die Form einer Kette von sich wiederholenden Modulen des neuronalen Netzes. In Standard-RNNs hat dieses sich wiederholende Modul eine sehr einfache Struktur, wie z.B. eine einzelne tanh-Schicht.
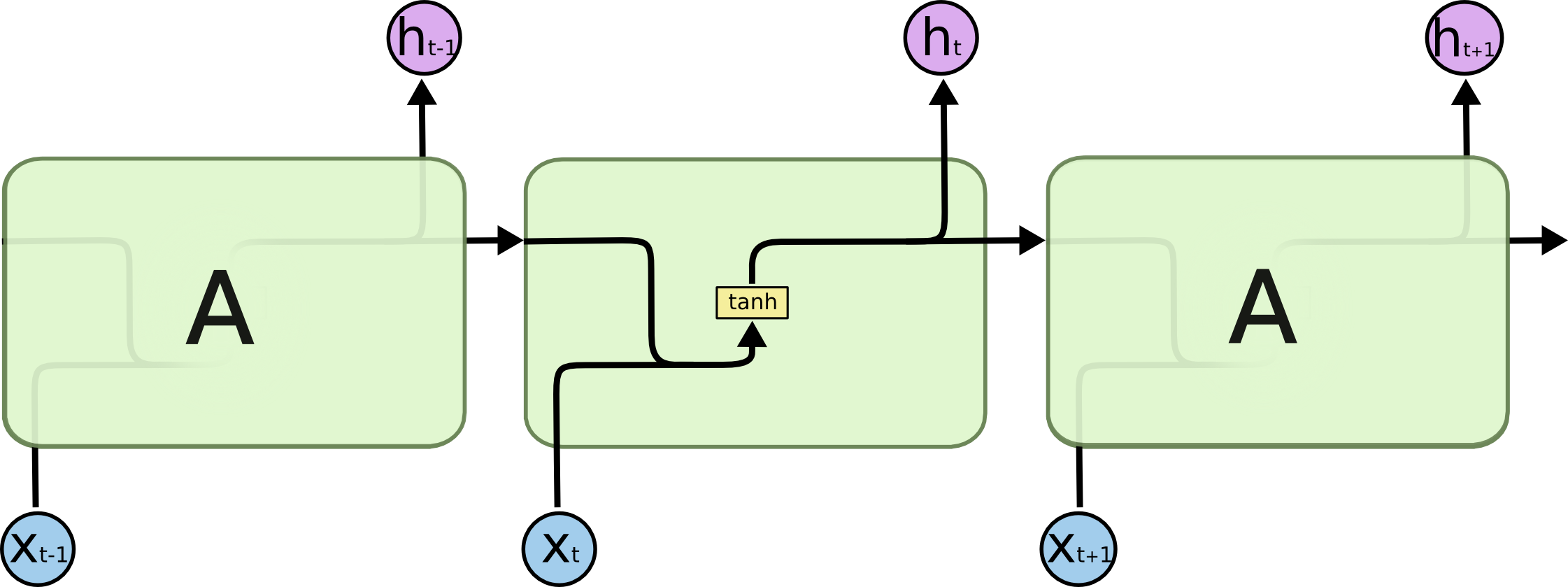
LSTMs haben ebenfalls diese kettenartige Struktur, aber das sich wiederholende Modul hat eine andere Struktur. Anstelle einer einzigen Schicht des neuronalen Netzes gibt es vier, die auf ganz besondere Weise interagieren.

Kümmern Sie sich nicht um die Details, was hier vor sich geht. Wir werden das LSTM-Diagramm später Schritt für Schritt durchgehen. Für den Moment wollen wir versuchen, uns mit der Notation vertraut zu machen, die wir verwenden werden.

Im obigen Diagramm trägt jede Linie einen ganzen Vektor, vom Ausgang eines Knotens zu den Eingängen der anderen. Die rosafarbenen Kreise stehen für punktuelle Operationen wie die Vektoraddition, während die gelben Kästchen gelernte Schichten des neuronalen Netzes darstellen. Zusammenlaufende Linien bedeuten Verkettung, während eine sich gabelnde Linie bedeutet, dass ihr Inhalt kopiert wird und die Kopien an verschiedene Stellen gehen.
Der Kerngedanke hinter LSTMs
Der Schlüssel zu LSTMs ist der Zellstatus, die horizontale Linie, die durch den oberen Teil des Diagramms verläuft.
Der Zellstatus ist eine Art Förderband. Er läuft geradlinig die gesamte Kette hinunter, mit nur einigen kleinen linearen Interaktionen. Es ist sehr einfach für Informationen, einfach unverändert entlang zu fließen.
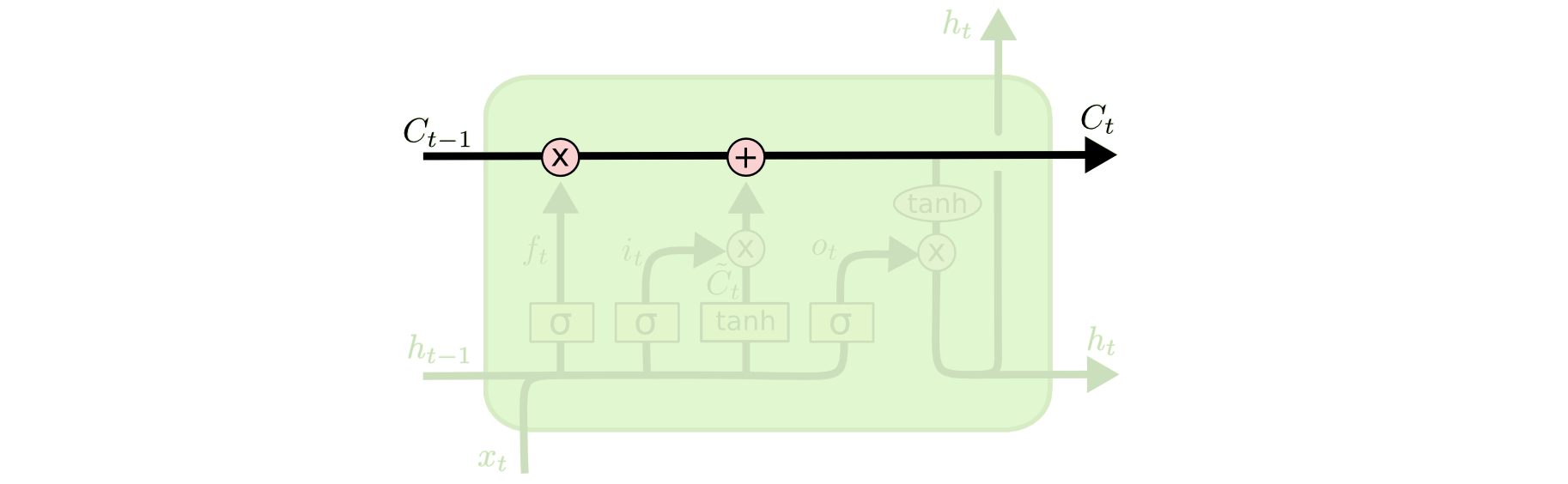
Das LSTM hat die Fähigkeit, Informationen aus dem Zellzustand zu entfernen oder ihm hinzuzufügen, sorgfältig reguliert durch Strukturen, die Gates genannt werden.
Gates sind eine Möglichkeit, optional Informationen durchzulassen. Sie bestehen aus einer sigmoidalen neuronalen Netzschicht und einer punktweisen Multiplikation.
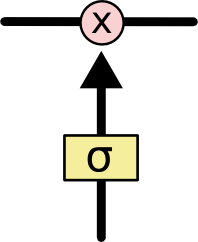
Die sigmoidale Schicht gibt Zahlen zwischen Null und Eins aus, die beschreiben, wie viel von jeder Komponente durchgelassen werden soll. Ein Wert von Null bedeutet „nichts durchlassen“, während ein Wert von Eins bedeutet „alles durchlassen!“
Ein LSTM hat drei dieser Gatter, um den Zellzustand zu schützen und zu kontrollieren.
Schrittweiser LSTM-Durchlauf
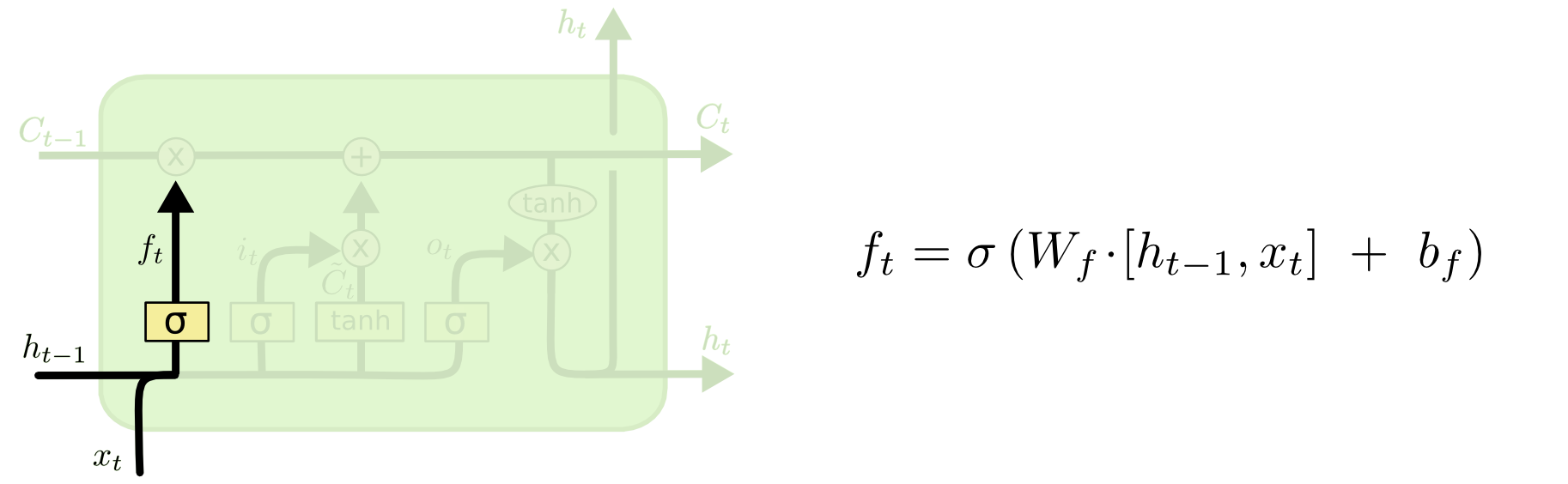
Der erste Schritt in unserem LSTM ist die Entscheidung, welche Informationen wir aus dem Zellzustand wegwerfen. Diese Entscheidung wird von einer sigmoidalen Schicht getroffen, die „forget gate layer“ genannt wird. Sie betrachtet \(h_{t-1}\) und \(x_t\) und gibt eine Zahl zwischen \(0\) und \(1\) für jede Zahl im Zellzustand \(C_{t-1}\) aus. Ein \(1\) steht für „vollständig beibehalten“, während ein \(0\) für „vollständig loswerden“ steht.
Wir kehren zu unserem Beispiel eines Sprachmodells zurück, das versucht, das nächste Wort auf der Grundlage aller vorherigen Wörter vorherzusagen. Bei einem solchen Problem könnte der Zellstatus das Geschlecht des aktuellen Subjekts enthalten, damit die richtigen Pronomen verwendet werden können. Wenn wir ein neues Subjekt sehen, wollen wir das Geschlecht des alten Subjekts vergessen.
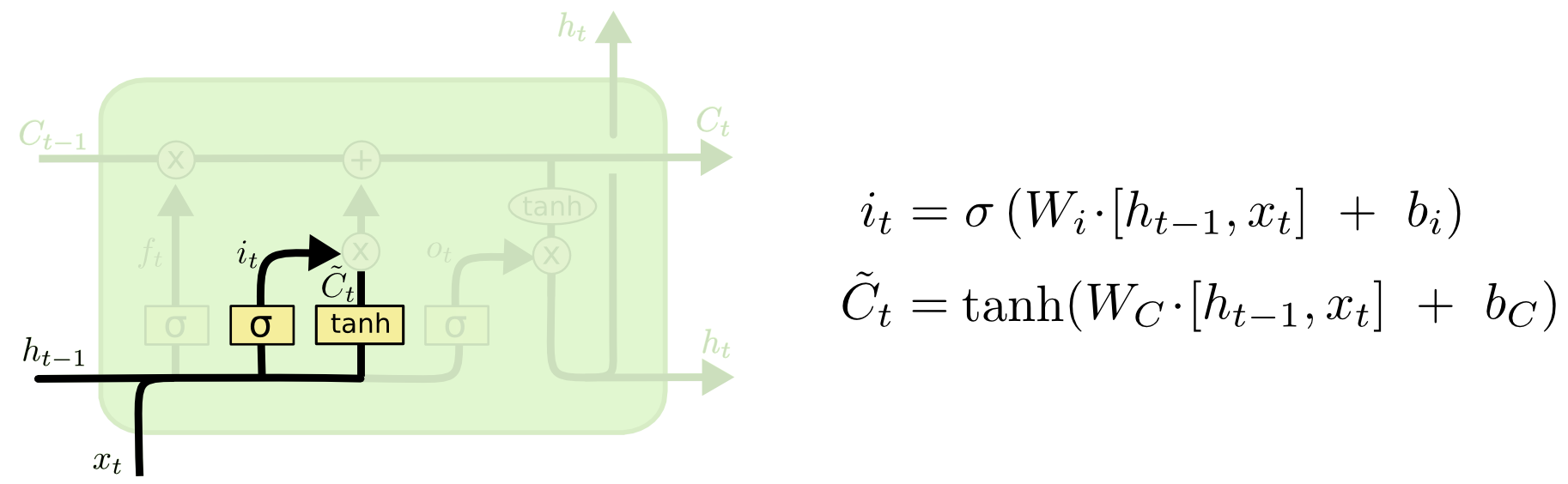
Der nächste Schritt besteht darin, zu entscheiden, welche neuen Informationen wir im Zellstatus speichern wollen. Dies besteht aus zwei Teilen. Zunächst entscheidet eine Sigmoid-Schicht, die so genannte „Input-Gate-Schicht“, welche Werte wir aktualisieren werden. Als Nächstes erstellt eine tanh-Schicht einen Vektor neuer Kandidatenwerte, \(\tilde{C}_t\), die dem Zustand hinzugefügt werden könnten. Im nächsten Schritt werden wir diese beiden kombinieren, um eine Aktualisierung des Zustands zu erstellen.
Im Beispiel unseres Sprachmodells würden wir das Geschlecht des neuen Subjekts zum Zellzustand hinzufügen wollen, um das alte zu ersetzen, das wir vergessen haben.
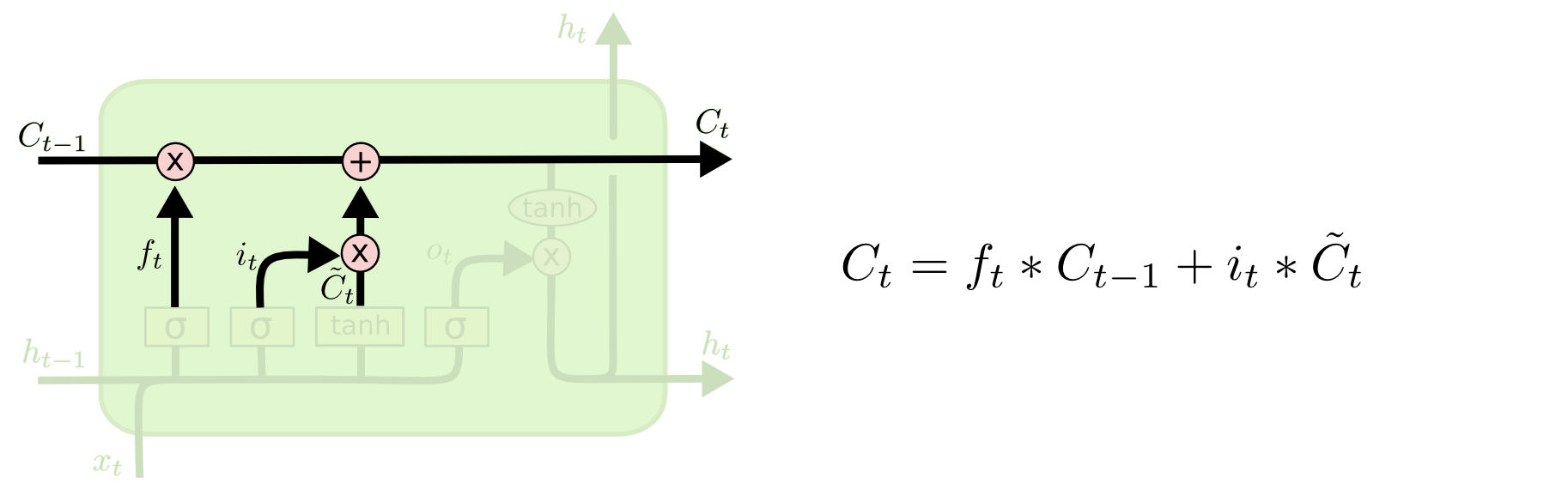
Es ist nun an der Zeit, den alten Zellzustand, \(C_{t-1}\), in den neuen Zellzustand \(C_t\) zu aktualisieren. In den vorangegangenen Schritten wurde bereits entschieden, was zu tun ist, wir müssen es nur noch umsetzen.
Wir multiplizieren den alten Zustand mit \(f_t\) und vergessen dabei die Dinge, die wir zuvor vergessen wollten. Dann addieren wir \(i_t*\tilde{C}_t\).
Im Falle des Sprachmodells würden wir an dieser Stelle die Informationen über das Geschlecht des alten Subjekts weglassen und die neuen Informationen hinzufügen, wie wir es in den vorherigen Schritten beschlossen haben.
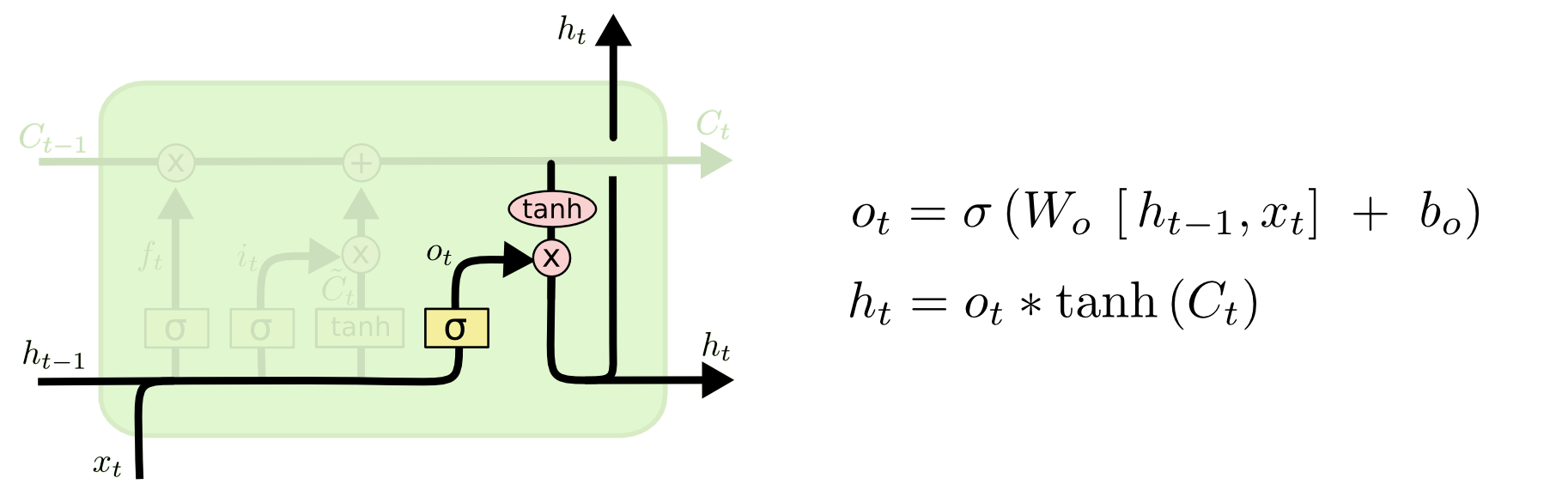
Schließlich müssen wir entscheiden, was wir ausgeben wollen. Diese Ausgabe wird auf unserem Zellstatus basieren, aber eine gefilterte Version sein. Zunächst führen wir eine Sigmoid-Schicht durch, die entscheidet, welche Teile des Zellstatus wir ausgeben werden. Dann lassen wir den Zellzustand durch \(\tanh\) laufen (um die Werte so zu verschieben, dass sie zwischen \(-1\) und \(1\) liegen) und multiplizieren ihn mit der Ausgabe des Sigmoid-Gatters, so dass wir nur die Teile ausgeben, für die wir uns entschieden haben.
Für das Sprachmodell-Beispiel könnte es, da es gerade ein Subjekt gesehen hat, Informationen ausgeben wollen, die für ein Verb relevant sind, für den Fall, dass es das ist, was als nächstes kommt. Es könnte zum Beispiel ausgeben, ob das Subjekt Singular oder Plural ist, damit wir wissen, in welche Form ein Verb konjugiert werden sollte, wenn das als nächstes kommt.
Varianten des Langzeitspeichers
Was ich bisher beschrieben habe, ist ein ziemlich normales LSTM. Aber nicht alle LSTMs sind so wie das oben beschriebene. Tatsächlich scheint es so, als ob fast jede Arbeit, die sich mit LSTMs beschäftigt, eine etwas andere Version verwendet. Die Unterschiede sind gering, aber es lohnt sich, einige von ihnen zu erwähnen.
Eine beliebte LSTM-Variante, die von Gers & Schmidhuber (2000) eingeführt wurde, ist das Hinzufügen von „Gucklochverbindungen“. Das bedeutet, dass wir die Gatterschichten den Zellzustand betrachten lassen.
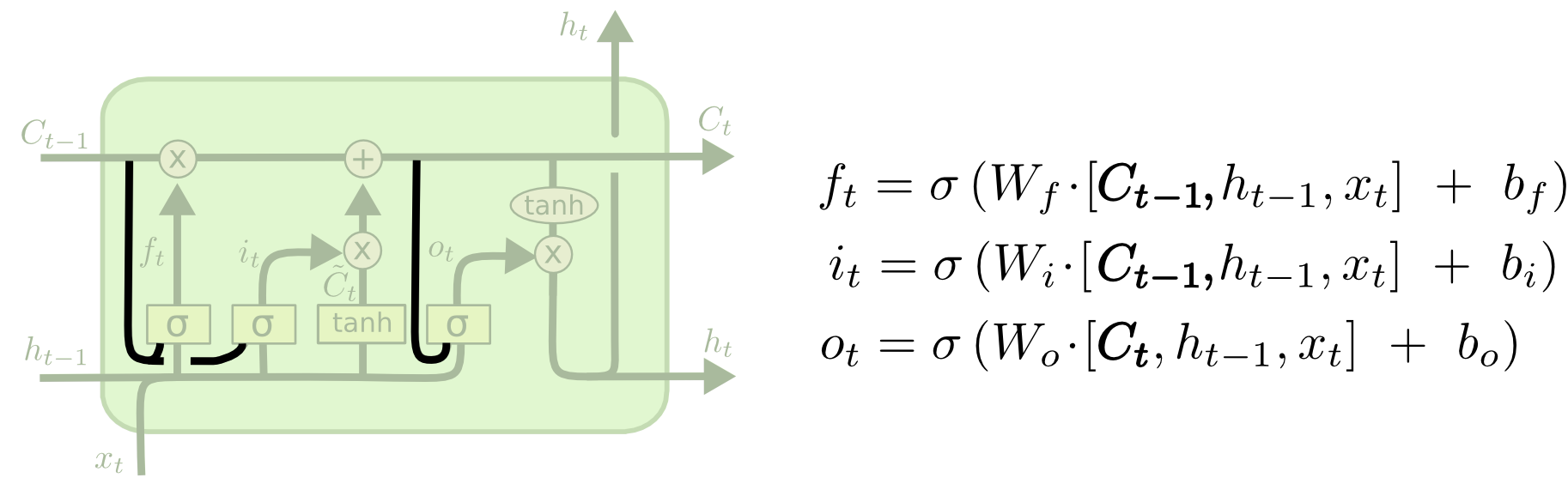
Das obige Diagramm fügt Gucklöcher zu allen Gattern hinzu, aber viele Arbeiten geben einige Gucklöcher an und andere nicht.
Eine andere Variante ist die Verwendung von gekoppelten Vergessens- und Eingabegattern. Anstatt separat zu entscheiden, was wir vergessen und was wir mit neuen Informationen versehen sollen, treffen wir diese Entscheidungen gemeinsam. Wir vergessen nur, wenn wir stattdessen etwas eingeben. Wir geben nur dann neue Werte in den Zustand ein, wenn wir etwas Älteres vergessen.
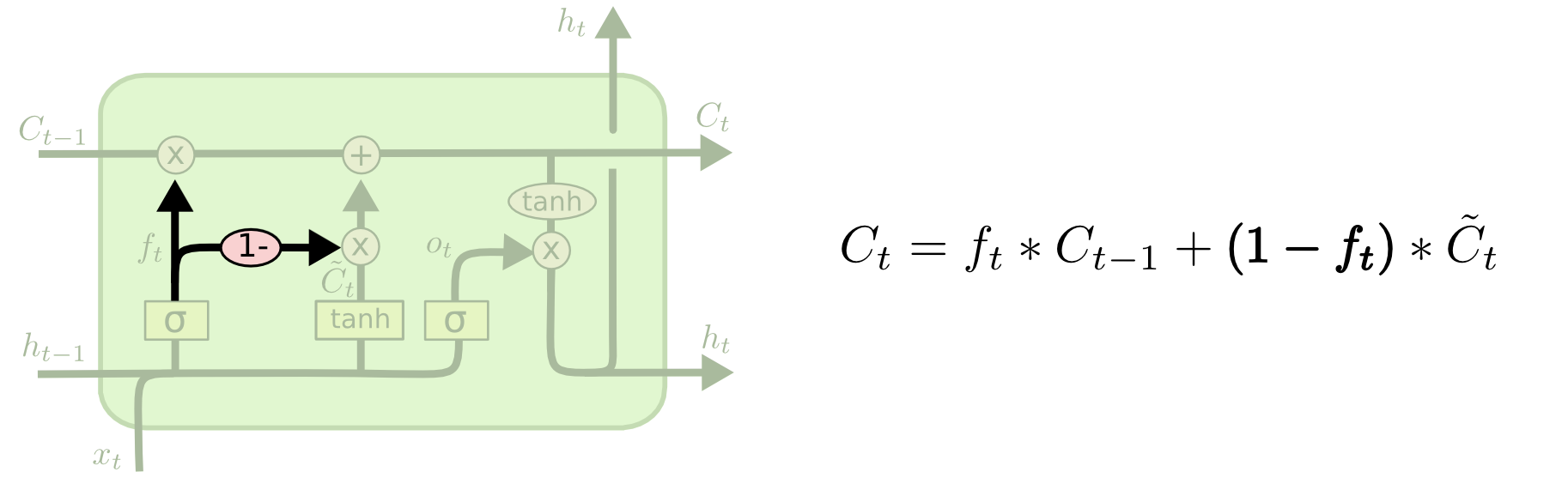
Eine etwas dramatischere Variante des LSTM ist die Gated Recurrent Unit (GRU), die von Cho et al. (2014) vorgestellt wurde. Sie kombiniert die Vergessens- und Eingabegatter zu einem einzigen „Aktualisierungsgatter“. Außerdem werden der Zellzustand und der verborgene Zustand zusammengeführt und einige andere Änderungen vorgenommen. Das daraus resultierende Modell ist einfacher als Standard-LSTM-Modelle und erfreut sich zunehmender Beliebtheit.

Dies sind nur einige der bekanntesten LSTM-Varianten. Es gibt viele andere, wie Depth Gated RNNs von Yao, et al. (2015). Es gibt auch einen völlig anderen Ansatz zur Bewältigung langfristiger Abhängigkeiten, wie Clockwork RNNs von Koutnik, et al. (2014).
Welche dieser Varianten ist die beste? Sind die Unterschiede von Bedeutung? Greff, et al. (2015) haben einen schönen Vergleich der populären Varianten durchgeführt und festgestellt, dass sie alle ungefähr gleich sind. Jozefowicz, et al. (2015) testeten mehr als zehntausend RNN-Architekturen und fanden einige, die bei bestimmten Aufgaben besser funktionierten als LSTMs.
Schlussfolgerung
Vorhin erwähnte ich die bemerkenswerten Ergebnisse, die Menschen mit RNNs erzielen. Im Wesentlichen werden alle diese Ergebnisse mit LSTMs erzielt. Sie sind für die meisten Aufgaben wirklich viel besser geeignet!
Aufgeschrieben als eine Reihe von Gleichungen, sehen LSTMs ziemlich einschüchternd aus. Ich hoffe, dass die schrittweise Erläuterung in diesem Aufsatz sie ein wenig zugänglicher gemacht hat.
LSTMs waren ein großer Schritt in dem, was wir mit RNNs erreichen können. Es liegt nahe, sich zu fragen: Gibt es einen weiteren großen Schritt? Eine verbreitete Meinung unter Forschern ist: „Ja! Es gibt einen nächsten Schritt und der heißt Aufmerksamkeit!“ Die Idee ist, dass jeder Schritt eines RNN Informationen aus einer größeren Sammlung von Informationen auswählt, um sie zu betrachten. Wenn Sie beispielsweise ein RNN verwenden, um eine Bildunterschrift zu erstellen, könnte es für jedes Wort, das es ausgibt, einen Teil des Bildes auswählen, den es untersuchen soll. Xu et al. (2015) machen genau das – das könnte ein interessanter Ausgangspunkt sein, wenn Sie die Aufmerksamkeit erforschen wollen! Es gibt eine Reihe wirklich aufregender Ergebnisse zur Nutzung von Aufmerksamkeit, und es scheint, als stünden noch viele weitere vor der Tür…
Aufmerksamkeit ist nicht das einzige spannende Thema in der RNN-Forschung. Die Grid-LSTMs von Kalchbrenner et al. (2015) scheinen zum Beispiel sehr vielversprechend zu sein. Arbeiten, die RNNs in generativen Modellen verwenden – wie Gregor, et al. (2015), Chung, et al. (2015), oder Bayer & Osendorfer (2015) – scheinen ebenfalls sehr interessant. Die letzten Jahre waren eine aufregende Zeit für rekurrente neuronale Netze, und die kommenden Jahre versprechen, noch aufregender zu werden!
Danksagungen
Ich bin einer Reihe von Personen dankbar, die mir geholfen haben, LSTMs besser zu verstehen, die Visualisierungen zu kommentieren und Feedback zu diesem Beitrag zu geben.
Ich bin meinen Kollegen bei Google sehr dankbar für ihr hilfreiches Feedback, insbesondere Oriol Vinyals, Greg Corrado, Jon Shlens, Luke Vilnis und Ilya Sutskever. Ich bin auch vielen anderen Freunden und Kollegen dankbar, die sich die Zeit genommen haben, mir zu helfen, darunter Dario Amodei und Jacob Steinhardt. Besonders dankbar bin ich Kyunghyun Cho für die äußerst aufmerksame Korrespondenz über meine Diagramme.
Vor diesem Beitrag habe ich die Erklärung von LSTMs in zwei Seminarreihen geübt, die ich über neuronale Netze gehalten habe. Ich danke allen, die daran teilgenommen haben, für ihre Geduld mit mir und für ihr Feedback.
-
Zusätzlich zu den ursprünglichen Autoren haben viele Menschen zum modernen LSTM beigetragen. Eine unvollständige Liste ist: Felix Gers, Fred Cummins, Santiago Fernandez, Justin Bayer, Daan Wierstra, Julian Togelius, Faustino Gomez, Matteo Gagliolo, und Alex Graves.
Weitere Beiträge
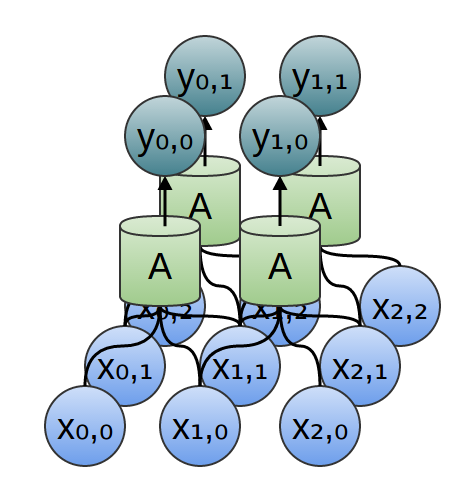
Attention und Augmented Recurrent Neural Networks
Auf Distill
Conv Nets
A Modular Perspective
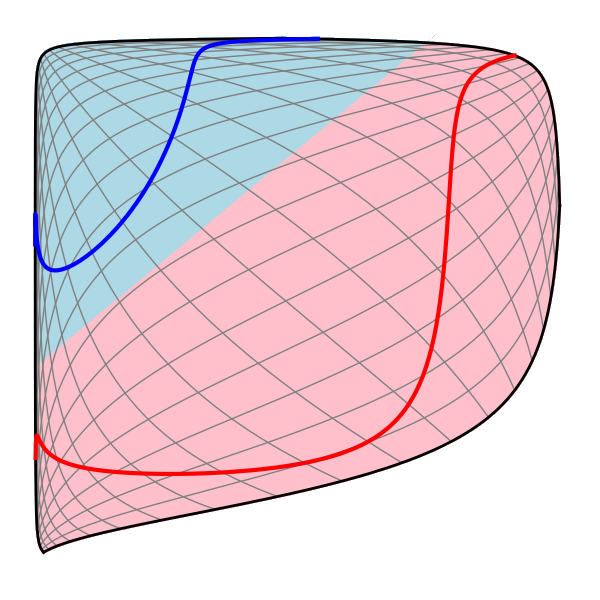
Neural Networks, Manifolds, and Topology