Gleichseitiges Dreieck konstruieren – MathBitsNotebook (Geo

Gleichseitiges Dreieck MathBitsNotebook.com Topical Outline | Geometry Outline | MathBits‘ Teacher Resources Terms of Use Contact Person: Donna Roberts

Benutze beim Zeichnen einer Konstruktion nur deinen Zirkel und dein Lineal. Kein Freihandzeichnen!

Wir werden DREI Konstruktionen eines gleichseitigen Dreiecks durchführen. Die erste besteht darin, ein gleichseitiges Dreieck mit der Länge einer Seite zu konstruieren, und die beiden anderen bestehen darin, ein gleichseitiges Dreieck zu konstruieren, das in einen Kreis eingeschrieben ist.

Gegeben: die Länge einer Seite des Dreiecks Konstruiere: ein gleichseitiges Dreieck

Schritte:
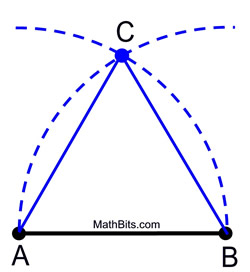
1. Lege deine Zirkelspitze auf A und messe den Abstand zu Punkt B. Schwinge einen Bogen dieser Größe über (oder unter) dem Segment.
2. Ohne die Spannweite des Zirkels zu ändern, lege die Zirkelspitze auf B und schwinge denselben Bogen, der sich mit dem ersten Bogen schneidet.
3. Bezeichne den Schnittpunkt als dritten Scheitelpunkt des gleichseitigen Dreiecks.

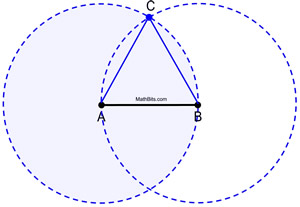
Sieh die Vollkreise bei der Arbeit.

Beweis der Konstruktion: Der Kreis A ist kongruent zum Kreis B, da sie beide mit der gleichen Radiuslänge AB gebildet wurden. Da AB und AC die Längen der Radien des Kreises A sind, sind sie gleich groß. In ähnlicher Weise sind AB und BC Radien des Kreises B, die einander gleich sind. Daher ist AB = AC = BC durch Substitution (oder transitive Eigenschaft). Da kongruente Segmente gleich lang sind, ist ΔABC gleichseitig (mit drei kongruenten Seiten).

Schritte:
1. Lege deine Zirkelspitze auf das Papier und zeichne einen Kreis. (Behalte diese Zirkelspanne bei!)
2. Setze einen Punkt mit der Bezeichnung A an eine beliebige Stelle des Kreisumfangs, der als Startpunkt dient.
3. Ohne die Spanne des Zirkels zu ändern, lege die Zirkelspitze auf A und schwinge einen kleinen Bogen über den Kreisumfang.
4. Ohne die Spanne des Zirkels zu ändern, bewege die Zirkelspitze zum Schnittpunkt des vorherigen Bogens und des Kreisumfangs und mache einen weiteren kleinen Bogen über den Kreisumfang.
5. Wiederhole diesen Prozess des „Schrittes“ um den Kreis herum, bis du zum Punkt A zurückkehrst.
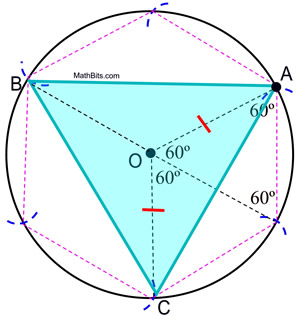
6. Beginne bei A und verbinde jeden anderen Bogen auf dem Kreis, um das gleichseitige Dreieck zu bilden.

Für weitere Informationen zum Beweis dieser Konstruktion siehe den Beweis eines eingeschriebenen regelmäßigen Sechsecks.

Beweis der Konstruktion: Der Beweis für das einbeschriebene regelmäßige Sechseck zeigt, dass die zentralen Winkel eines regelmäßigen Sechsecks 60º enthalten. Die zentralen Winkel des Dreiecks, das in diesen Kreis einbeschrieben ist, enthalten 120º. Da ΔAOC gleichschenklig ist (OA und OC sind Radienlängen), ist m∠OCA = m∠OAC = ½ (180 – 120) = 30º. ΔAOC ΔCOB ΔBOA durch SAS. Durch CPCTC ergibt sich ∠OCB ∠OCA und m∠OCB = 30º durch Substitution und m∠BCA = 60º. In ähnlicher Weise ergibt sich m∠ACB = m∠CBA = m∠BAC = 60º und gleichseitiges ΔABC.

SCHRITTE:
1. Lege deine Zirkelspitze auf das Papier und zeichne einen Kreis, O. (Behalte diese Zirkelspanne bei!)
2. Zeichne mit einem Lineal einen Durchmesser des Kreises und beschrifte die Endpunkte P und B.
3. Ohne die Zirkelspanne zu verändern, lege die Zirkelspitze auf P und zeichne einen Vollkreis.
4. Beschrifte die Schnittpunkte der beiden Kreisumfänge mit A und C.
5. Zeichne Segmente von A nach B, B nach C und C nach A, um das gleichseitige Dreieck zu bilden.

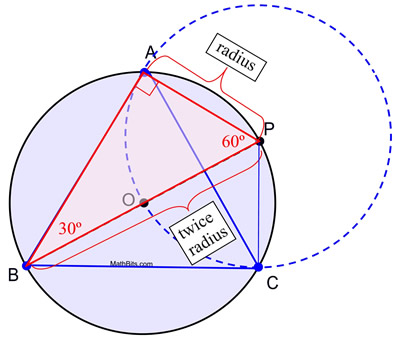
Beweis der Konstruktion: Diese Konstruktion nutzt die Tatsache, dass ein in einen Halbkreis eingeschriebener Winkel ein rechter Winkel ist und dass in einem 30º-60º-90º-Dreieck die Länge des kurzen Schenkels die Hälfte der Länge der Hypotenuse ist. In dieser Konstruktion sind der Kreis O und der Kreis P kongruent, da sie die gleiche Radiuslänge haben. AP ist eine Radiuslänge des Kreises P und die Radien AP = OP. OP ist ebenfalls eine Radiuslänge des Kreises O (zusammen mit OB) und der Durchmesser BP = BO + OP = 2 OP. Durch Substitution ergibt sich BP = 2 AP, womit die Voraussetzungen für m∠ABP = 30º gegeben sind. Folglich ist m∠APB = 60º. Ein ähnliches Argument kann verwendet werden, um festzustellen, dass für ΔPBC m∠PBC = 30º und m∠BPC = 60º, was ΔPBC ΔPBA durch ASA (mit gemeinsamer Seite von B nach P) macht.
Nun, , da sie die entsprechenden Seiten der beiden kongruenten Dreiecke sind, was ΔABC gleichschenklig macht. ∠BAC ∠BCA, da die Basiswinkel eines gleichschenkligen Dreiecks kongruent sind.
m∠ABC = m∠ABP + m∠PBC = 30º + 30º = 60º durch Winkeladditionspostulat und Substitution. m∠BAC + m∠BCA + m∠ABC = 180º, weil die Summe der Winkelmaße in einem Dreieck 180º beträgt. Da m∠BAC + m∠BAC + 60º = 180º durch Substitution, wissen wir, dass 2m∠BAC = 120º und m∠BAC = 60º ist. Folglich ist m∠BCA durch Substitution ebenfalls gleich 60º, so dass ΔABC gleichseitig ist.