Einführung in die Klein-Flasche

Wenn du gerne trinkst, dann ist die Klein-Flasche kein empfehlenswertes Gefäß. Sie sieht zwar vage wie eine Flasche aus, aber sie umschließt kein Volumen, was bedeutet, dass sie eigentlich keine Flüssigkeit aufnehmen kann. Was auch immer man „hineinschüttet“, kommt einfach wieder heraus.

Wie konstruiert man so ein seltsames Ding und warum sollte man es konstruieren? Der Mathematiker Felix Klein, der die Flasche 1882 entdeckte, beschrieb sie als eine Fläche, „die man sich vorstellen kann, indem man ein Stück eines Gummischlauchs umdreht und es durch sich selbst hindurchgehen lässt, so dass sich Außen und Innen treffen“.

Ihr Browser unterstützt das Video-Tag nicht.Direktlink

Es ist offensichtlich, dass die Klein-Flasche, genau wie die bekanntere Kugel, eine geschlossene Fläche ist: Sie ist endlich in dem Sinne, dass man sie in einen endlichen Bereich des Raums einpassen kann, aber eine Ameise könnte ewig auf ihr herumlaufen, ohne jemals auf eine Grenze zu stoßen oder über eine Kante zu fallen. Im Gegensatz zur Kugel, die ein Innen und ein Außen hat, ist die Klein-Flasche einseitig: Beim Herumlaufen könnte unsere Ameise beide Seiten jedes Punktes der Oberfläche erreichen. Das ist der Grund, warum die Flasche kein Volumen einschließt, und es beantwortet auch die Frage nach dem „Warum“: Die Klein-Flasche ist interessant, weil wir in der Natur nicht viele einseitige Formen finden. (Ein weiteres sehr schönes Bild einer Klein-Flasche finden Sie hier.)

Das Möbiusband ist einseitig – sehen Sie sich die animierte Version an. (Bild und Animation von Konrad Polthier.)

Wenn das ein bisschen verwirrend ist, dann denke an ein einfacheres Beispiel für eine einseitige Fläche: das berühmte Möbiusband. Man kann es herstellen, indem man zwei Enden eines Papierstreifens nimmt, den Streifen verdreht und dann die Enden zusammenklebt. Wenn du einen Papierstreifen nimmst, dessen beide Seiten unterschiedliche Farben haben, zum Beispiel grün und orange, kannst du dich leicht davon überzeugen, dass das entstehende Möbiusband einseitig ist. Wenn man es einmal gedreht und geklebt hat, wird man feststellen, dass man jeden orangefarbenen Punkt von jedem grünen Punkt aus erreichen kann, ohne das Papier durchstechen oder über den Rand klettern zu müssen.

Im Gegensatz zur Klein-Flasche hat das Möbiusband eine Grenze – sie besteht aus den beiden nicht geklebten Kanten des ursprünglichen Streifens. Aber es gibt eine Verbindung zwischen den beiden. Wenn man zwei Möbiusbänder nimmt und eine geschlossene Form erzeugt, indem man ihre Grenzen mit einem gewöhnlichen zweiseitigen Band verbindet, wie unten gezeigt, erhält man genau die Klein-Flasche.

Ihr Browser unterstützt das Video-Tag nicht.Direktlink

Diese Tatsache inspirierte den Mathematiker Leo Moser zu einem Limerick:

Ein Mathematiker namens KleinDachte, das Möbiusband sei göttlich.Sagte er: „

Einige Mathematiker sind wirklich vielseitig begabt!

Eine weitere merkwürdige Eigenschaft der Klein-Flasche ist, dass sie sich selbst schneidet, was bedeutet, dass es schwierig ist, sie aus einem einzigen Gummischlauch herzustellen, wie Klein vorgeschlagen hat. Streng genommen handelt es sich bei dem oben abgebildeten sich selbst schneidenden Objekt nicht um eine Klein-Flasche, sondern (wie Klein andeutete) nur um eine Visualisierung einer solchen. Um zu verstehen, warum, denken Sie zunächst an den bekannteren Doughnut (mathematisch als Torus bezeichnet). Man kann einen Torus aus einer quadratischen Gummiplatte herstellen, indem man zunächst zwei gegenüberliegende Seiten zu einem Zylinder verklebt und dann die beiden Randkomponenten dieses Zylinders zusammenklebt, um den Torus zu erhalten.

Herstellung eines Torus: Zuerst klebt man gegenüberliegende Punkte auf zwei gegenüberliegenden Seiten des Quadrats, um einen Zylinder zu bilden, und dann klebt man die beiden Begrenzungskreise dieses Zylinders (entsprechend dem Kleben gegenüberliegender Punkte auf den beiden verbleibenden Seiten des Quadrats), um einen Torus zu bilden.

Wenn man sich die Mühe des Klebens nicht machen will, kann man sich den Torus einfach als ein Quadrat vorstellen, wobei man bedenken muss, dass gegenüberliegende Punkte auf gegenüberliegenden Seiten als gleich betrachtet werden. Wenn du also eine auf dem „Quadrat“ gezeichnete Form über die obere Kante schiebst, wird sie an der unteren Kante wieder erscheinen und wenn du sie über die rechte Kante schiebst, wird sie an der linken Kante wieder erscheinen (und umgekehrt).

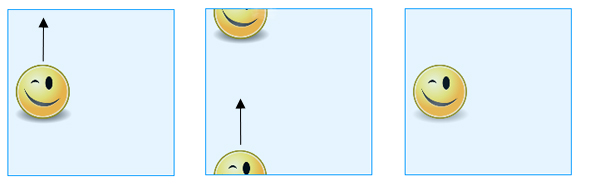
Wenn du eine auf dem „Quadrat“ gezeichnete Form über die obere Kante schiebst, wird sie an der unteren Kante wieder erscheinen.

Um eine echte Klein-Flasche zu erhalten, beginne auf die gleiche Weise, indem du gegenüberliegende Punkte auf einem Paar gegenüberliegender Seiten eines Quadrats bestimmst. Für das andere Seitenpaar bestimmt man jedoch nicht die Punkte, die sich direkt gegenüberliegen, sondern die Punkte, die sich diagonal gegenüberliegen, wie in der Abbildung gezeigt.

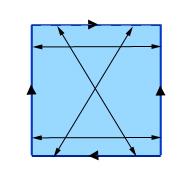
Bau einer Klein-Flasche: Bestimme die gegenüberliegenden Punkte von zwei gegenüberliegenden Seiten (die senkrechten in dieser Abbildung) und dann die diagonal gegenüberliegenden Punkte auf den verbleibenden zwei Seiten. (Wenn du die Punkte auf der oberen und unteren Seite von links nach rechts mit den Zahlen 0 bis 1 beschriftest, dann wird ein Punkt mit der Bezeichnung x auf der oberen Seite mit dem Punkt mit der Bezeichnung 1-x auf der unteren Seite identifiziert.)

Das resultierende Objekt ist die Klein-Flasche. Auch hier kann man sich die Flasche als ein Quadrat vorstellen, wobei zu beachten ist, welche Begrenzungspunkte als gleichwertig betrachtet werden. Wenn Sie eine Form über eine der Kanten schieben, an denen gegenüberliegende Punkte identifiziert wurden (in unserem Bild vertikal), erscheint sie auf der gegenüberliegenden Seite wieder, wie zuvor. Wenn man sie jedoch über eine der Kanten schiebt, deren Punkte diagonal identifiziert wurden (in unserem Bild horizontal), erscheint sie auf der gegenüberliegenden Seite, aber verschoben und als Spiegelbild ihres ursprünglichen Selbst.

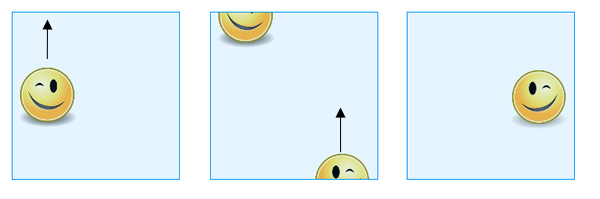
Wenn man eine Form über die obere Kante schiebt, erscheint sie auf der unteren Kante, aber auf der anderen Seite und als Spiegelbild ihres ursprünglichen Selbst.

Die einzige Möglichkeit, diese Form im dreidimensionalen Raum zu bauen, indem man tatsächlich Punkte zusammenklebt, ist, sie sich selbst schneiden zu lassen. Dies läuft darauf hinaus, Paare von Punkten im Inneren des ursprünglichen Quadrats zu identifizieren, so dass die resultierende Form streng genommen nicht genau dieselbe ist wie die Klein-Flasche, bei der nur die Randpunkte identifiziert wurden. Es ist nur eine Möglichkeit, die Flasche im dreidimensionalen Raum darzustellen (es gibt auch andere).

Kurioserweise hängen die Begriffe „innen“, „außen“ und „Einseitigkeit“ von dem Umgebungsraum ab, in dem sich ein Objekt befindet. Eine Schleife, die auf einem Stück Papier (im zweidimensionalen Raum) gezeichnet wird, hat zum Beispiel ein klar definiertes Innen und Außen, aber eine Schleife, die im dreidimensionalen Raum gezeichnet wird, nicht. Aus diesem Grund können wir nicht von Einseitigkeit sprechen, wenn wir nicht zuerst entscheiden, wie wir eine Fläche in den dreidimensionalen Raum einbetten. Es gibt jedoch eine eng verwandte Eigenschaft, die einer Form innewohnt und nicht vom umgebenden Raum abhängt. Eine Fläche wird als ausrichtbar bezeichnet, wenn man eine auf ihr gezeichnete Form nicht so verschieben kann, dass sie wie ihr eigenes Spiegelbild aussieht, und auch nicht an ihren Ausgangspunkt zurückkehren kann. Wie Sie in der Animation zum Bild rechts sehen können, ist das Möbiusband nicht ausrichtbar. Und wie du auf dem Bild mit dem Smiley oben sehen kannst, ist auch die Klein-Flasche nicht ausrichtbar, denn die Klein-Flasche ist eine geschlossene, nicht ausrichtbare Fläche. Um mehr darüber zu erfahren, siehe den Artikel Inside the Klein bottle.

Über den Autor

Marianne Freiberger ist Redakteurin bei Plus.