Bevor wir beginnen, müssen wir einige Annahmen treffen.
Erstens, wir arbeiten mit Newtonschen Flüssigkeiten. Dies ist die einfachste mathematische Methode, um die Viskosität in einer Flüssigkeit zu berücksichtigen. Es gibt keine realen Flüssigkeiten, die perfekt unter diese Kategorie fallen, aber in den meisten Fällen können Luft und Wasser als Newtonsche Flüssigkeiten behandelt werden. Die andere sehr wichtige Hypothese, die wir aufstellen, ist, dass die Flüssigkeit inkompressibel ist. Das bedeutet, dass seine Dichte, rho, eine Konstante ist.
Massenerhaltung

Die erste Gleichung besagt, dass die Masse der Flüssigkeit, mit der wir arbeiten, erhalten bleibt. Die Flüssigkeit kann ihre Form ändern, aber diese Gleichung sagt uns, dass die Masse von Anfang bis Ende gleich bleibt.
Lassen Sie uns nun über Mathematik sprechen. Der Buchstabe u steht für die Geschwindigkeit der Flüssigkeit und ist ein Vektor. Er hat drei Komponenten, die wir u, v und w nennen können und die die Geschwindigkeit der Flüssigkeit in x-, y- und z-Richtung darstellen. Der griechische Buchstabe nabla ∇ gefolgt von einem Punkt ist der Divergenzoperator. Das bedeutet, dass wir seine Komponenten in jeder Richtung (in diesem Fall x, y, z) differenzieren müssen.

Die erste Ableitung sagt uns, wie sich die x-Komponente der Geschwindigkeit ändert, wenn wir uns in x-Richtung bewegen. Das Gleiche gilt für die beiden anderen Ableitungen. Da diese Gleichung gleich Null ist, zeigt sie uns, dass die Masse erhalten bleibt.
Drehmomenterhaltung

Die zweite Gleichung ist eigentlich ein Satz von drei Differentialgleichungen. Sie kann als das zweite Newtonsche Gesetz für Flüssigkeiten beschrieben werden. Wenn wir den Ausdruck erweitern, erhalten wir ein komplexes System.
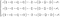
Da sie viel einfacher zu verstehen ist, werden wir uns auf die nicht erweiterte Impulserhaltung konzentrieren.
Wenn wir mit Flüssigkeiten arbeiten, können wir sagen, dass Masse und Dichte dasselbe sind (solange ihr Volumen dasselbe ist). Wenn wir zwei Flüssigkeiten betrachten, können wir sagen, dass die dichtere Flüssigkeit die „schwerere“ ist (z.B. Quecksilber und Wasser). In diesem Fall ist der griechische Buchstabe ρ (rho) die Dichte der Flüssigkeit.
Wir haben die Masse, jetzt brauchen wir, um zum zweiten Newtonschen Gesetz zurückzukehren, die Beschleunigung. Diese ist genau das Ergebnis der zeitlichen Ableitung des Geschwindigkeitsvektors.

Jetzt bleiben nur noch die Terme auf der rechten Seite des Gleichheitszeichens übrig, und diese stellen alle Kräfte dar, die auf die Flüssigkeit einwirken.
Der erste Term ∇p ist der Gradient des Drucks. Er stellt den Druckunterschied in dem Raum dar, in dem die Flüssigkeit enthalten ist. Wenn es zum Beispiel eine Zone mit niedrigem Druck und eine andere mit höherem Druck gibt, bewegt sich das Fluid vom Hochdruckbereich zum niedrigeren. Der Gradient von p sagt all das aus.
Der zweite Term beschreibt die Viskosität des Fluids. Stell dir zwei verschiedene Flüssigkeiten vor, zum Beispiel Wasser und Honig. Wenn du ein Glas Wasser einschenkst, fällt es schnell und leicht. Wenn du das Gleiche mit Honig machst, ist er klebrig und fließt sehr langsam. Das besagt dieser Ausdruck.
Der letzte Term, F, ist der einfachste, weil er alle äußeren Kräfte darstellt, die auf die Flüssigkeit einwirken können. Normalerweise ist die Kraft, die wir hier betrachten, die Schwerkraft.
Das ist es, all diese ausgefallenen Symbole und Buchstaben bedeuten einfach Kraft = Masse x Beschleunigung.
Verwendung der Navier-Stokes-Gleichungen
Da das Lösen dieser Gleichungen so kompliziert ist, müssen wir eine Menge Näherungen machen, um sie zu verwenden. Einige Beispiele sind die Poiseuille- und die Couette-Strömung. Diesen beiden Wissenschaftlern ist es unter vielen Annahmen gelungen, eine Lösung der Navier-Stokes-Gleichungen für eine ganz bestimmte Anwendung zu finden. Wenn wir sie jedoch für eine kompliziertere Aufgabe, wie die Wettervorhersage, verwenden wollen, müssen wir etwas anderes tun.
Die gebräuchlichste Art, diese Gleichungen zu verwenden, ist ihre Umformung mit dem Reynolds-Mittelwert. Dies ist ein fortgeschrittener mathematischer Prozess und das Ergebnis sind die Reynolds-Gleichungen. Sie werden in der Regel als RANS-Gleichungen (Reynolds-gemittelte Navier-Stokes-Gleichungen) bezeichnet.
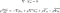
Diese Gleichungen werden verwendet, wenn sich das Fluid in einer turbulenten Strömung befindet. Sie sehen fast genauso aus wie die Navier-Stokes-Gleichungen, mit Ausnahme des letzten Terms. Dieser wird als Reynolds-Spannungstensor bezeichnet. Er ist die Größe, die es uns ermöglicht, die Turbulenz im Fluid zu berücksichtigen.
In den RANS-Gleichungen werden die von uns verwendeten Größen über ein Zeitintervall gemittelt. Dieses Intervall muss klein genug sein, um die Beobachtung des zu untersuchenden Phänomens zu ermöglichen. Gleichzeitig muss es groß genug sein, damit der Turbulenzeffekt an Bedeutung verliert.
Mit den richtigen Annahmen funktionieren diese Gleichungen. Wir wissen, wie man sie einsetzt, um Formel-1-Autos schneller zu machen, um ein Raumschiff zur ISS zu bringen und um die Wettervorhersage zu machen. Sie fragen sich vielleicht, warum der Beweis dieser Gleichungen eine Million Dollar wert ist?
Eine Million Dollar Preis
Physikalisch gesehen sind diese Gleichungen einfach das zweite Newtonsche Gesetz, das mit Flüssigkeiten funktioniert. Wenn wir einige Annahmen und Vereinfachungen machen, können wir erstaunliche Dinge mit ihnen machen.
Das eigentliche Problem ist folgendes. Diese Gleichungen ohne Näherungen zu lösen, ist einfach furchtbar kompliziert. Es ist so schwierig, dass noch nicht bewiesen ist, dass die Lösungen tatsächlich existieren. Und hier kommt der Millenniumspreis ins Spiel.
Die offizielle Aufgabenstellung (hier zu finden) lautet:
Beweisen Sie oder geben Sie ein Gegenbeispiel für die folgende Aussage: In drei Raumdimensionen und in der Zeit gibt es bei einem anfänglichen Geschwindigkeitsfeld einen Geschwindigkeitsvektor und ein skalares Druckfeld, die beide glatt und global definiert sind und die Navier-Stokes-Gleichungen lösen.
Das bedeutet, dass man drei Dinge tun muss, um den Preis zu gewinnen:
- Beweisen, dass eine Lösung existiert
- Die Lösung muss in jedem Punkt des Raumes existieren
- Die Lösung muss glatt sein. Das bedeutet, dass eine kleine Änderung der Anfangsbedingungen nur eine kleine Veränderung des Ergebnisses zur Folge hat.
Für einen Ingenieur ist es normalerweise ausreichend zu wissen, dass diese Gleichungen funktionieren, wenn auch nur bis zu einem gewissen Grad der Annäherung. Für einen Mathematiker ist es jedoch sehr wichtig zu wissen, ob die Lösungen existieren und wie sie sich verhalten.
Vielleicht denken Sie jetzt, dass, wenn sie so funktionieren, wie sie sind, die Zeit und Energie für die Suche nach einem Beweis reine Zeitverschwendung ist. Nun, wie bei vielen technologischen Fortschritten in der Geschichte der Menschheit mag das Ergebnis nicht sehr wichtig erscheinen. Was wichtig ist, ist der Weg dorthin, der neues Wissen und Verbesserungen für unser Leben bringen kann.
Denken Sie an Weltraummissionen. Wenn die Menschen nie beschlossen hätten, den Mond zu betreten, gäbe es viele Gegenstände nicht, die unser Leben verbessern. MRT-Geräte und Herzschrittmacher stammen aus Technologien, die für die Weltraumforschung entwickelt wurden. Heute setzen Ärzte auf der ganzen Welt sie täglich ein, um Leben zu retten. Das Gleiche gilt auch hier. Der Weg zur Lösung der Navier-Stokes-Gleichungen wird uns helfen, unser Verständnis von Flüssigkeiten und mehr zu verbessern. Er kann uns zu neuen Entdeckungen führen und wird wahrscheinlich die Erfindung neuer mathematischer Verfahren erfordern. Diese kann dann verwendet werden, um viele andere Probleme zu lösen und neue Technologien zu erfinden, die unser Leben verbessern und uns besser machen.