Introduction
Stellen Sie sich vor: Sie sollen den Preis des nächsten iPhones prognostizieren und haben dafür historische Daten erhalten. Dazu gehören Merkmale wie vierteljährliche Verkäufe, monatliche Ausgaben und eine ganze Reihe von Dingen, die mit der Bilanz von Apple zusammenhängen. Welcher Art von Problem würden Sie als Datenwissenschaftler diese Aufgabe zuordnen? Natürlich die Zeitreihenmodellierung.
Von der Vorhersage des Absatzes eines Produkts bis zur Schätzung des Stromverbrauchs von Haushalten gehört die Zeitreihenvorhersage zu den Kernkompetenzen, die jeder Datenwissenschaftler beherrschen sollte, wenn nicht sogar muss. Es gibt eine Fülle verschiedener Techniken, die Sie verwenden können, und wir werden in diesem Artikel eine der effektivsten, Auto ARIMA genannt, behandeln.

Wir werden zunächst das Konzept von ARIMA verstehen, das uns zu unserem Hauptthema – Auto ARIMA – führen wird. Um unsere Konzepte zu festigen, werden wir einen Datensatz aufnehmen und ihn sowohl in Python als auch in R implementieren.
Inhaltsverzeichnis
- Was ist eine Zeitreihe?
- Methoden zur Zeitreihenvorhersage
- Einführung in ARIMA
- Schritte zur ARIMA-Implementierung
- Warum brauchen wir AutoARIMA?
- Auto-ARIMA-Implementierung (am Datensatz für Fluggäste)
- Wie wählt Auto-ARIMA die Parameter aus?
Wenn Sie mit Zeitreihen und ihren Techniken (wie gleitender Durchschnitt, exponentielle Glättung und ARIMA) vertraut sind, können Sie direkt zu Abschnitt 4 übergehen. Anfänger sollten mit dem folgenden Abschnitt beginnen, der eine kurze Einführung in Zeitreihen und verschiedene Vorhersagetechniken enthält.
Was ist eine Zeitreihe?
Bevor wir uns mit den Techniken zur Bearbeitung von Zeitreihendaten befassen, müssen wir zunächst verstehen, was eine Zeitreihe eigentlich ist und wie sie sich von anderen Datenarten unterscheidet. Hier ist die formale Definition von Zeitreihen: Es handelt sich um eine Reihe von Datenpunkten, die in gleichbleibenden Zeitabständen gemessen werden. Das bedeutet einfach, dass bestimmte Werte in einem konstanten Intervall aufgezeichnet werden, das stündlich, täglich, wöchentlich, alle 10 Tage usw. sein kann. Der Unterschied zwischen Zeitreihen besteht darin, dass jeder Datenpunkt in der Reihe von den vorhergehenden Datenpunkten abhängig ist. Lassen Sie uns den Unterschied anhand einiger Beispiele deutlicher verstehen.
Beispiel 1:
Angenommen, Sie haben einen Datensatz von Personen, die bei einem bestimmten Unternehmen einen Kredit aufgenommen haben (wie in der Tabelle unten dargestellt). Glauben Sie, dass jede Zeile mit den vorherigen Zeilen in Beziehung steht? Sicherlich nicht! Der Kredit, den eine Person aufgenommen hat, basiert auf ihren finanziellen Bedingungen und Bedürfnissen (es könnte noch andere Faktoren geben, wie die Größe der Familie usw., aber der Einfachheit halber betrachten wir nur das Einkommen und die Art des Kredits). Außerdem wurden die Daten nicht in einem bestimmten Zeitintervall erhoben. Sie hängen davon ab, wann das Unternehmen einen Kreditantrag erhalten hat.

Beispiel 2:
Lassen Sie uns ein anderes Beispiel nehmen. Nehmen wir an, Sie haben einen Datensatz, der den CO2-Gehalt der Luft pro Tag enthält (Screenshot unten). Können Sie die ungefähre CO2-Menge für den nächsten Tag vorhersagen, indem Sie die Werte der letzten paar Tage betrachten? Nun, natürlich. Wie Sie sehen, wurden die Daten täglich aufgezeichnet, d.h. das Zeitintervall ist konstant (24 Stunden).

Sie haben sicher schon eine Ahnung davon bekommen – der erste Fall ist ein einfaches Regressionsproblem und der zweite ein Zeitreihenproblem. Das Zeitreihenproblem kann zwar auch mit Hilfe der linearen Regression gelöst werden, aber das ist nicht wirklich der beste Ansatz, da dabei die Beziehung der Werte zu allen relativen Vergangenheitswerten vernachlässigt wird. Schauen wir uns nun einige der gängigen Techniken an, die zur Lösung von Zeitreihenproblemen verwendet werden.
Methoden für die Zeitreihenprognose
Es gibt eine Reihe von Methoden für die Zeitreihenprognose, die wir in diesem Abschnitt kurz behandeln werden. Die ausführliche Erklärung und Python-Codes für alle unten genannten Techniken finden Sie in diesem Artikel: 7 Techniken für Zeitreihenprognosen (mit Python-Codes).
- Naiver Ansatz: Bei dieser Prognosetechnik wird vorhergesagt, dass der Wert des neuen Datenpunktes gleich dem des vorherigen Datenpunktes ist. Das Ergebnis wäre eine flache Linie, da alle neuen Werte die vorherigen Werte übernehmen.
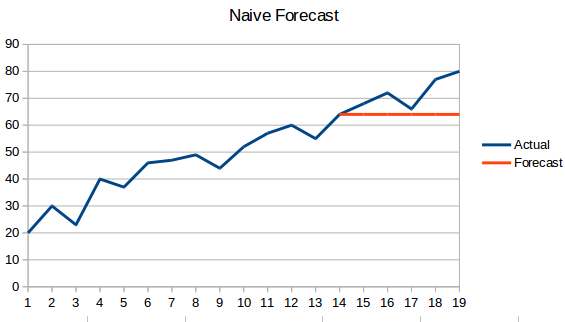
- Einfacher Durchschnitt: Der nächste Wert wird als Durchschnitt aller vorherigen Werte genommen. Die Vorhersagen sind hier besser als beim „Naiven Ansatz“, da er keine flache Linie ergibt, aber hier werden alle vergangenen Werte berücksichtigt, was nicht immer sinnvoll ist. Wenn Sie zum Beispiel die heutige Temperatur vorhersagen sollen, würden Sie eher die Temperatur der letzten 7 Tage als die Temperatur vor einem Monat berücksichtigen.

- Gleitender Durchschnitt: Dies ist eine Verbesserung gegenüber der vorherigen Technik. Anstatt den Durchschnitt aller vorherigen Punkte zu nehmen, wird der Durchschnitt von ’n‘ vorherigen Punkten als vorhergesagter Wert genommen.

- Gewichteter gleitender Durchschnitt : Ein gewichteter gleitender Durchschnitt ist ein gleitender Durchschnitt, bei dem die vergangenen ’n‘ Werte unterschiedlich gewichtet werden.

- Einfache exponentielle Glättung: Bei dieser Technik werden jüngere Beobachtungen stärker gewichtet als Beobachtungen aus der fernen Vergangenheit.

- Lineares Trendmodell von Holt: Bei dieser Methode wird der Trend des Datensatzes berücksichtigt. Unter Trend versteht man die zunehmende oder abnehmende Natur der Reihe. Angenommen, die Zahl der Buchungen in einem Hotel steigt jedes Jahr, dann kann man sagen, dass die Zahl der Buchungen einen steigenden Trend aufweist. Die Prognosefunktion bei dieser Methode ist eine Funktion von Niveau und Trend.

- Holt-Winters-Methode: Dieser Algorithmus berücksichtigt sowohl den Trend als auch die Saisonalität der Reihe. Beispiel: Die Anzahl der Buchungen in einem Hotel ist an Wochenenden hoch & an Wochentagen niedrig und nimmt jedes Jahr zu; es gibt eine wöchentliche Saisonalität und einen zunehmenden Trend.

- ARIMA: ARIMA ist eine sehr beliebte Technik zur Modellierung von Zeitreihen. Es beschreibt die Korrelation zwischen Datenpunkten und berücksichtigt die Differenz der Werte. Eine Verbesserung von ARIMA ist SARIMA (oder saisonales ARIMA). Im folgenden Abschnitt werden wir ARIMA etwas ausführlicher betrachten.
Einführung in ARIMA
In diesem Abschnitt werden wir eine kurze Einführung in ARIMA geben, die für das Verständnis von Auto Arima hilfreich sein wird. Eine ausführliche Erklärung von Arima, Parametern (p,q,d), Plots (ACF PACF) und Implementierung ist in diesem Artikel enthalten: Komplettes Tutorial zu Zeitreihen.
ARIMA ist eine sehr beliebte statistische Methode für Zeitreihenprognosen. ARIMA steht für Auto-Regressive Integrated Moving Averages. ARIMA-Modelle gehen von folgenden Annahmen aus: –
- Die Datenreihe ist stationär, was bedeutet, dass sich der Mittelwert und die Varianz nicht mit der Zeit verändern sollten. Eine Reihe kann durch Log-Transformation oder Differenzierung der Reihe stationär gemacht werden.
- Die als Eingabe bereitgestellten Daten müssen eine univariate Reihe sein, da Arima die vergangenen Werte verwendet, um die zukünftigen Werte vorherzusagen.
ARIMA hat drei Komponenten – AR (autoregressiver Term), I (differenzierender Term) und MA (gleitender Durchschnittsterm). Jede dieser Komponenten ist zu verstehen:
- Der AR-Term bezieht sich auf die vergangenen Werte, die für die Vorhersage des nächsten Wertes verwendet werden. Der AR-Term wird durch den Parameter „p“ in arima definiert. Der Wert von ‚p‘ wird mit Hilfe des PACF-Plots bestimmt.
- MA-Term wird verwendet, um die Anzahl der vergangenen Prognosefehler zu definieren, die zur Vorhersage der zukünftigen Werte verwendet werden. Der Parameter ‚q‘ in arima stellt den MA-Term dar. Die ACF-Darstellung wird verwendet, um den richtigen ‚q‘-Wert zu ermitteln.
- Die Reihenfolge der Differenzierung gibt an, wie oft die Differenzierungsoperation an der Reihe durchgeführt wird, um sie stationär zu machen. Tests wie ADF und KPSS können verwendet werden, um festzustellen, ob die Reihe stationär ist, und helfen bei der Ermittlung des d-Wertes.
Schritte zur ARIMA-Implementierung
Die allgemeinen Schritte zur Implementierung eines ARIMA-Modells sind –
- Laden der Daten: Der erste Schritt zur Modellbildung ist natürlich das Laden des Datensatzes
- Vorverarbeitung: Je nach Datensatz werden die Schritte der Vorverarbeitung festgelegt. Dazu gehören die Erstellung von Zeitstempeln, die Konvertierung des Datentyps der Datums-/Zeitspalte, die Herstellung der Univariabilität der Reihe usw.
- Herstellung der Stationarität der Reihe: Um die Annahme zu erfüllen, muss die Reihe stationär gemacht werden. Dazu gehört die Überprüfung der Stationarität der Reihe und die Durchführung der erforderlichen Transformationen
- Bestimmen des d-Wertes: Um die Reihe stationär zu machen, wird die Anzahl der durchgeführten Differenzoperationen als d-Wert genommen
- Erstellen von ACF- und PACF-Diagrammen: Dies ist der wichtigste Schritt bei der ARIMA-Implementierung. ACF-PACF-Plots werden verwendet, um die Eingabeparameter für unser ARIMA-Modell zu bestimmen
- Bestimmen Sie die p- und q-Werte: Lesen Sie die Werte von p und q aus den Diagrammen im vorherigen Schritt ab
- Passen Sie das ARIMA-Modell an: Passen Sie das ARIMA-Modell unter Verwendung der verarbeiteten Daten und der in den vorherigen Schritten berechneten Parameterwerte an
- Sagen Sie die Werte im Validierungsset voraus: Vorhersage der zukünftigen Werte
- Berechnung des RMSE: Um die Leistung des Modells zu überprüfen, prüfen Sie den RMSE-Wert anhand der Vorhersagen und der tatsächlichen Werte im Validierungsset
Warum brauchen wir Auto-ARIMA?
Obwohl ARIMA ein sehr leistungsfähiges Modell für die Vorhersage von Zeitreihendaten ist, sind die Prozesse der Datenvorbereitung und der Parameterabstimmung sehr zeitaufwendig. Bevor Sie ARIMA implementieren, müssen Sie die Reihe stationär machen und die Werte von p und q anhand der oben besprochenen Diagramme bestimmen. Auto-ARIMA macht diese Aufgabe für uns wirklich einfach, da die Schritte 3 bis 6, die wir im vorherigen Abschnitt gesehen haben, entfallen. Im Folgenden finden Sie die Schritte, die Sie für die Implementierung von Auto-ARIMA befolgen sollten:
- Laden Sie die Daten: Dieser Schritt wird der gleiche sein. Laden Sie die Daten in Ihr Notebook
- Vorverarbeitung der Daten: Die Eingabe sollte univariat sein, also lassen Sie die anderen Spalten weg
- Auto ARIMA anpassen: Passen Sie das Modell an die univariaten Reihen an
- Vorhersagen von Werten auf der Validierungsmenge: Machen Sie Vorhersagen auf der Validierungsmenge
- Berechnen Sie den RMSE: Überprüfen Sie die Leistung des Modells anhand der vorhergesagten Werte im Vergleich zu den tatsächlichen Werten
Wie Sie sehen, haben wir die Auswahl der p- und q-Merkmale vollständig umgangen. Was für eine Erleichterung! Im nächsten Abschnitt werden wir Auto-ARIMA anhand eines Spielzeugdatensatzes implementieren.
Implementierung in Python und R
Wir werden den International-Air-Passenger-Datensatz verwenden. Dieser Datensatz enthält die monatliche Gesamtzahl der Passagiere (in Tausend). Er hat zwei Spalten – Monat und Anzahl der Passagiere. Sie können den Datensatz über diesen Link herunterladen.
#load the datadata = pd.read_csv('international-airline-passengers.csv')#divide into train and validation settrain = datavalid = data#preprocessing (since arima takes univariate series as input)train.drop('Month',axis=1,inplace=True)valid.drop('Month',axis=1,inplace=True)#plotting the datatrain.plot()valid.plot()

#building the modelfrom pyramid.arima import auto_arimamodel = auto_arima(train, trace=True, error_action='ignore', suppress_warnings=True)model.fit(train)forecast = model.predict(n_periods=len(valid))forecast = pd.DataFrame(forecast,index = valid.index,columns=)#plot the predictions for validation setplt.plot(train, label='Train')plt.plot(valid, label='Valid')plt.plot(forecast, label='Prediction')plt.show()

#calculate rmsefrom math import sqrtfrom sklearn.metrics import mean_squared_errorrms = sqrt(mean_squared_error(valid,forecast))print(rms)
output -76.51355764316357
Nachfolgend finden Sie den R-Code für dasselbe Problem:
# loading packageslibrary(forecast)library(Metrics)# reading datadata = read.csv("international-airline-passengers.csv")# splitting data into train and valid setstrain = datavalid = data# removing "Month" columntrain$Month = NULL# training modelmodel = auto.arima(train)# model summarysummary(model)# forecastingforecast = predict(model,44)# evaluationrmse(valid$International.airline.passengers, forecast$pred)
Wie wählt Auto Arima die besten Parameter aus
Im obigen Code haben wir einfach den .fit(), um das Modell anzupassen, ohne die Kombination von p, q, d auswählen zu müssen. Aber wie hat das Modell die beste Kombination dieser Parameter ermittelt? Auto ARIMA berücksichtigt die generierten AIC- und BIC-Werte (wie Sie im Code sehen können), um die beste Parameterkombination zu ermitteln. AIC- (Akaike Information Criterion) und BIC-Werte (Bayesian Information Criterion) sind Schätzer zum Vergleich von Modellen. Je niedriger diese Werte sind, desto besser ist das Modell.
Sehen Sie sich diese Links an, wenn Sie sich für die Mathematik hinter AIC und BIC interessieren.
Endnoten und weiterführende Literatur
Ich habe festgestellt, dass Auto-ARIMA die einfachste Technik zur Durchführung von Zeitreihenprognosen ist. Es ist gut, eine Abkürzung zu kennen, aber es ist auch wichtig, mit der Mathematik dahinter vertraut zu sein. In diesem Artikel habe ich die Einzelheiten der Funktionsweise von ARIMA kurz erläutert, aber lesen Sie unbedingt die im Artikel angegebenen Links. Hier noch einmal die Links:
- Ein umfassender Leitfaden für Anfänger zur Zeitreihenprognose in Python
- Komplettes Tutorial zu Zeitreihen in R
- 7 Techniken für die Zeitreihenprognose (mit Python-Codes)
Ich würde vorschlagen, das hier Gelernte an diesem Übungsproblem zu üben: Übungsproblem zu Zeitreihen. Sie können auch unseren Schulungskurs zum gleichen Übungsproblem, Zeitreihenvorhersage, besuchen, um sich einen Vorsprung zu verschaffen.