Beginner's Guide to Feature Selection in Python

Wenn Sie mehr über Python lernen wollen, besuchen Sie den kostenlosen Kurs „Intro to Python for Data Science“ von DataCamp.

Sie alle kennen Datensätze. Manchmal sind sie klein, aber oft sind sie auch ungeheuer groß. Es ist sehr schwierig, sehr große Datensätze zu verarbeiten, zumindest so groß, dass es zu einem Engpass bei der Verarbeitung kommt.

Warum sind diese Datensätze dann so groß? Nun, es sind die Merkmale. Je größer die Anzahl der Merkmale, desto größer die Datensätze. Nun, nicht immer. Es gibt Datensätze, bei denen die Anzahl der Merkmale sehr hoch ist, aber sie enthalten nicht so viele Instanzen. Aber das ist hier nicht der Punkt der Diskussion. Man könnte sich also fragen, wie man mit einem handelsüblichen Computer diese Art von Datensätzen verarbeiten kann, ohne sich in die Quere zu kommen.

Oft bleiben in einem hochdimensionalen Datensatz einige völlig irrelevante, unbedeutende und unwichtige Merkmale übrig. Es hat sich gezeigt, dass der Beitrag dieser Arten von Merkmalen zur prädiktiven Modellierung im Vergleich zu den kritischen Merkmalen oft geringer ist. Sie können auch gar keinen Beitrag leisten. Diese Merkmale verursachen eine Reihe von Problemen, die wiederum den Prozess der effizienten prädiktiven Modellierung verhindern –

• Unnötige Ressourcenzuweisung für diese Merkmale.
• Diese Merkmale wirken wie ein Rauschen, bei dem das maschinelle Lernmodell sehr schlecht abschneiden kann.
• Das maschinelle Modell benötigt mehr Zeit, um trainiert zu werden.

Was ist also die Lösung? Die wirtschaftlichste Lösung ist die Merkmalsauswahl.

Die Merkmalsauswahl ist der Prozess der Auswahl der wichtigsten Merkmale aus einem gegebenen Datensatz. In vielen Fällen kann die Feature Selection auch die Leistung eines maschinellen Lernmodells verbessern.

Hört sich interessant an, oder?

Sie haben eine informelle Einführung in die Feature Selection und ihre Bedeutung in der Welt der Datenwissenschaft und des maschinellen Lernens erhalten. In diesem Beitrag werden Sie behandeln:

• Einführung in die Feature Selection und Verständnis ihrer Bedeutung
• Unterschied zwischen Feature Selection und Dimensionalitätsreduktion
• Unterschiedliche Arten von Feature Selection Methoden
• Implementierung verschiedener Feature Selection Methoden mit scikit-.learn

Einführung in die Merkmalsauswahl

Die Merkmalsauswahl wird auch als Variablenauswahl oder Attributauswahl bezeichnet.

Im Wesentlichen ist es der Prozess der Auswahl der wichtigsten/relevantesten.

Die Bedeutung der Merkmalsauswahl

Die Bedeutung der Merkmalsauswahl lässt sich am besten erkennen, wenn man mit einem Datensatz arbeitet, der eine große Anzahl von Merkmalen enthält. Diese Art von Datensatz wird oft als hochdimensionaler Datensatz bezeichnet. Diese hohe Dimensionalität bringt eine Reihe von Problemen mit sich, wie z.B. – diese hohe Dimensionalität erhöht die Trainingszeit Ihres maschinellen Lernmodells erheblich, sie kann Ihr Modell sehr kompliziert machen, was wiederum zu Overfitting führen kann.

Oftmals gibt es in einem hochdimensionalen Merkmalssatz mehrere Merkmale, die redundant sind, d.h. diese Merkmale sind nichts anderes als Erweiterungen der anderen wesentlichen Merkmale. Diese redundanten Merkmale tragen auch nicht effektiv zur Modellbildung bei. Es besteht also eindeutig die Notwendigkeit, die wichtigsten und relevantesten Merkmale für einen Datensatz zu extrahieren, um die effektivste Vorhersageleistung bei der Modellierung zu erzielen.

„Das Ziel der Variablenauswahl ist dreifach: Verbesserung der Vorhersageleistung der Prädiktoren, Bereitstellung schnellerer und kostengünstigerer Prädiktoren und besseres Verständnis des zugrunde liegenden Prozesses, der die Daten erzeugt hat.“

-Einführung in die Variablen- und Merkmalsauswahl

Lassen Sie uns nun den Unterschied zwischen Dimensionalitätsreduktion und Merkmalsauswahl verstehen.

Gelegentlich wird die Merkmalsauswahl mit der Dimensionalitätsreduktion verwechselt. Aber sie sind verschieden. Die Merkmalsauswahl unterscheidet sich von der Dimensionalitätsreduktion. Beide Methoden neigen dazu, die Anzahl der Attribute im Datensatz zu reduzieren, aber eine Dimensionalitätsreduktionsmethode tut dies, indem sie neue Kombinationen von Attributen schafft (manchmal als Feature-Transformation bekannt), während Feature-Selection-Methoden die in den Daten vorhandenen Attribute einschließen und ausschließen, ohne sie zu verändern.

Einige Beispiele für Dimensionalitätsreduktionsmethoden sind die Hauptkomponentenanalyse, die Singulärwertzerlegung, die lineare Diskriminanzanalyse usw.

Lassen Sie mich die Bedeutung der Merkmalsauswahl für Sie zusammenfassen:

• Sie ermöglicht es dem Algorithmus für maschinelles Lernen, schneller zu trainieren.
• Sie reduziert die Komplexität eines Modells und macht es einfacher zu interpretieren.
• Sie verbessert die Genauigkeit eines Modells, wenn die richtige Teilmenge ausgewählt wird.
• Sie reduziert Overfitting.

Im nächsten Abschnitt werden die verschiedenen Arten allgemeiner Merkmalsauswahlmethoden untersucht – Filtermethoden, Wrapper-Methoden und eingebettete Methoden.

Filtermethoden

Das folgende Bild beschreibt filterbasierte Merkmalsauswahlmethoden am besten:

Bildquelle: Analytics Vidhya

Die Filtermethode stützt sich auf die allgemeine Einzigartigkeit der auszuwertenden Daten und wählt eine Teilmenge von Merkmalen aus, ohne einen Mining-Algorithmus einzubeziehen. Die Filtermethode verwendet das genaue Bewertungskriterium, das Abstand, Information, Abhängigkeit und Konsistenz umfasst. Die Filtermethode verwendet die Hauptkriterien der Ranking-Technik und nutzt die Rangordnungsmethode für die Variablenauswahl. Der Grund für die Verwendung der Rangordnungsmethode ist die Einfachheit und die Erzeugung ausgezeichneter und relevanter Merkmale. Die Rangordnungsmethode filtert irrelevante Merkmale heraus, bevor der Klassifizierungsprozess beginnt.

Filtermethoden werden im Allgemeinen als Vorverarbeitungsschritt für Daten verwendet. Die Auswahl der Merkmale ist unabhängig von einem maschinellen Lernalgorithmus. Die Merkmale werden auf der Grundlage statistischer Werte eingestuft, die die Korrelation der Merkmale mit der Ergebnisvariablen bestimmen. Korrelation ist ein stark kontextabhängiger Begriff, der von Arbeit zu Arbeit variiert. In der folgenden Tabelle können Sie Korrelationskoeffizienten für verschiedene Datentypen (in diesem Fall kontinuierlich und kategorisch) definieren.

Bildquelle: Analytics Vidhya

Beispiele für einige Filtermethoden sind der Chi-Quadrat-Test, der Informationsgewinn und die Korrelationskoeffizienten.

Als Nächstes sehen Sie Wrapper-Methoden.

Wrapper-Methoden

Wie bei den Filter-Methoden gibt es auch hier eine Infografik, die Ihnen helfen wird, Wrapper-Methoden besser zu verstehen:

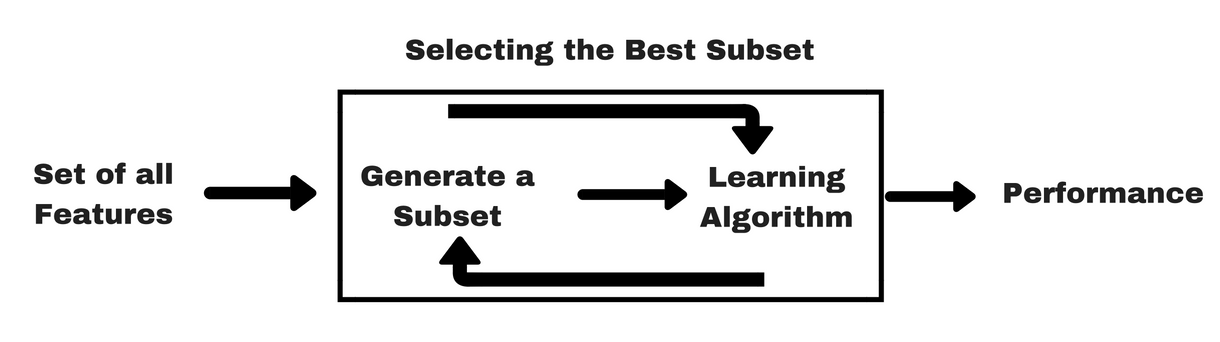
Bildquelle: Analytics Vidhya

Wie Sie in der obigen Abbildung sehen können, benötigt eine Wrapper-Methode einen maschinellen Lernalgorithmus und verwendet dessen Leistung als Bewertungskriterium. Diese Methode sucht nach einem Merkmal, das für den maschinellen Lernalgorithmus am besten geeignet ist, und zielt darauf ab, die Mining-Leistung zu verbessern. Zur Bewertung der Merkmale wird die Vorhersagegenauigkeit für Klassifizierungsaufgaben und die Güte von Clustern mit Hilfe von Clustering bewertet.

Einige typische Beispiele für Wrapper-Methoden sind die Vorwärtsauswahl von Merkmalen, die Rückwärtsauswahl von Merkmalen, die rekursive Auswahl von Merkmalen usw.

• Vorwärtsauswahl: Das Verfahren beginnt mit einer leeren Menge von Merkmalen . Das beste der ursprünglichen Merkmale wird ermittelt und der reduzierten Menge hinzugefügt. Bei jeder weiteren Iteration wird das beste der verbleibenden Originalattribute der Menge hinzugefügt.
• Rückwärtseliminierung: Das Verfahren beginnt mit der vollständigen Menge der Attribute. Bei jedem Schritt wird das schlechteste Attribut, das in der Menge verbleibt, entfernt.
• Kombination von Vorwärtsauswahl und Rückwärtseliminierung: Die schrittweise Vorwärtsselektion und die Rückwärtselimination können so kombiniert werden, dass bei jedem Schritt das beste Attribut ausgewählt und das schlechteste aus den verbleibenden Attributen entfernt wird.
• Rekursive Merkmalseliminierung: Die rekursive Merkmalseliminierung führt eine gierige Suche durch, um die beste Merkmalsuntergruppe zu finden. Sie erstellt iterativ Modelle und bestimmt bei jeder Iteration das beste oder das schlechteste Merkmal. Die nachfolgenden Modelle werden mit den verbleibenden Merkmalen erstellt, bis alle Merkmale erforscht sind. Anschließend werden die Merkmale nach der Reihenfolge ihrer Eliminierung geordnet. Im schlimmsten Fall, wenn ein Datensatz eine Anzahl von N Merkmalen enthält, führt RFE eine gierige Suche nach 2N Kombinationen von Merkmalen durch.

Gut genug!

Lassen Sie uns nun eingebettete Methoden untersuchen.

Eingebettete Methoden

Eingebettete Methoden sind iterativ in dem Sinne, dass sie sich um jede Iteration des Modelltrainings kümmern und sorgfältig jene Merkmale extrahieren, die am meisten zum Training für eine bestimmte Iteration beitragen. Regularisierungsmethoden sind die am häufigsten verwendeten eingebetteten Methoden, die ein Merkmal mit einem Schwellenwert für den Koeffizienten bestrafen.

Deshalb werden Regularisierungsmethoden auch als Bestrafungsmethoden bezeichnet, die zusätzliche Einschränkungen in die Optimierung eines Vorhersagealgorithmus (z. B. eines Regressionsalgorithmus) einführen, die das Modell in Richtung einer geringeren Komplexität (weniger Koeffizienten) verzerren.

Beispiele für Regularisierungsalgorithmen sind LASSO, Elastic Net, Ridge Regression usw.

Unterschied zwischen Filter- und Wrapper-Methoden

Die Unterscheidung zwischen Filtermethoden und Wrapper-Methoden in Bezug auf ihre Funktionalitäten kann manchmal verwirrend sein. Werfen wir einen Blick auf die Punkte, in denen sie sich voneinander unterscheiden.

• Filtermethoden beinhalten kein maschinelles Lernmodell, um zu bestimmen, ob ein Merkmal gut oder schlecht ist, während Wrapper-Methoden ein maschinelles Lernmodell verwenden und das Merkmal trainieren, um zu entscheiden, ob es wichtig ist oder nicht.
• Filtermethoden sind im Vergleich zu Wrapper-Methoden viel schneller, da sie kein Training der Modelle beinhalten. Auf der anderen Seite sind Wrapper-Methoden rechenintensiv, und im Falle massiver Datensätze sind Wrapper-Methoden nicht die effektivste Methode zur Auswahl von Merkmalen.
• Filter-Methoden können in Situationen, in denen es nicht genügend Daten gibt, um die statistische Korrelation der Merkmale zu modellieren, nicht die beste Teilmenge von Merkmalen finden, aber Wrapper-Methoden können aufgrund ihrer erschöpfenden Natur immer die beste Teilmenge von Merkmalen liefern.
• Die Verwendung von Merkmalen aus Wrapper-Methoden in Ihrem endgültigen Modell für maschinelles Lernen kann zu einer Überanpassung führen, da Wrapper-Methoden bereits Modelle für maschinelles Lernen mit den Merkmalen trainieren, was die tatsächliche Leistungsfähigkeit des Lernens beeinträchtigt. Aber die Merkmale von Filtermethoden führen in den meisten Fällen nicht zu einer Überanpassung

So weit haben Sie die Bedeutung der Merkmalsauswahl untersucht und ihren Unterschied zur Dimensionalitätsreduktion verstanden. Sie haben auch verschiedene Arten von Merkmalsauswahlmethoden behandelt. So weit, so gut!

Sehen wir uns nun einige Fallen an, in die man bei der Merkmalsauswahl tappen kann:

Wichtige Überlegungen

Sie haben vielleicht schon verstanden, welchen Wert die Merkmalsauswahl in einer Pipeline für maschinelles Lernen hat und welche Leistungen sie erbringt, wenn sie integriert wird. Aber es ist sehr wichtig zu verstehen, an welcher Stelle genau Sie die Merkmalsauswahl in Ihre Pipeline für maschinelles Lernen integrieren sollten.

Einfach gesagt, sollten Sie den Schritt der Merkmalsauswahl einbeziehen, bevor Sie die Daten zum Training in das Modell einspeisen, insbesondere wenn Sie Methoden zur Genauigkeitsschätzung wie die Kreuzvalidierung verwenden. Dadurch wird sichergestellt, dass die Merkmalsauswahl für die Datenfaltung unmittelbar vor dem Training des Modells durchgeführt wird. Wenn Sie jedoch zuerst die Merkmalsauswahl durchführen, um Ihre Daten vorzubereiten, und dann die Modellauswahl und das Training auf den ausgewählten Merkmalen durchführen, wäre das ein Fehler.

Wenn Sie die Merkmalsauswahl für alle Daten durchführen und dann eine Kreuzvalidierung vornehmen, wurden die Testdaten in jeder Falte des Kreuzvalidierungsverfahrens auch für die Auswahl der Merkmale verwendet, und dies führt tendenziell zu einer Verzerrung der Leistung Ihres maschinellen Lernmodells.

Genug der Theorien! Kommen wir gleich zum Programmieren.

Eine Fallstudie in Python

Für diese Fallstudie werden Sie den Datensatz Pima-Indianer Diabetes verwenden. Die Beschreibung des Datensatzes finden Sie hier.

Der Datensatz entspricht einer Klassifikationsaufgabe, bei der Sie anhand von 8 Merkmalen vorhersagen müssen, ob eine Person Diabetes hat.

Der Datensatz enthält insgesamt 768 Beobachtungen. Ihre erste Aufgabe besteht darin, den Datensatz zu laden, damit Sie fortfahren können. Aber vorher importieren wir die notwendigen Abhängigkeiten, die Sie benötigen werden. Die anderen können Sie nach und nach importieren.

import pandas as pdimport numpy as np

Nun, da die Abhängigkeiten importiert sind, laden wir den Pima-Indianer-Datensatz mit Hilfe der Pandas-Bibliothek in ein Dataframe-Objekt.

data = pd.read_csv("diabetes.csv")

Der Datensatz wurde erfolgreich in das Dataframe-Objekt Daten geladen. Werfen wir nun einen Blick auf die Daten.

data.head()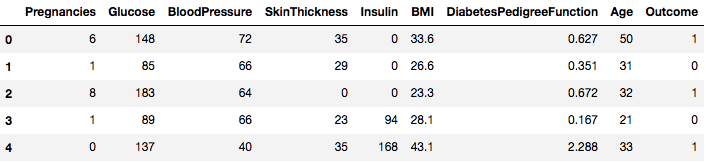

Sie sehen also 8 verschiedene Merkmale, die mit den Ergebnissen 1 und 0 gekennzeichnet sind, wobei 1 bedeutet, dass die Beobachtung Diabetes hat, und 0 bedeutet, dass die Beobachtung keinen Diabetes hat. Es ist bekannt, dass der Datensatz fehlende Werte enthält. Insbesondere fehlen Beobachtungen für einige Spalten, die mit einem Nullwert gekennzeichnet sind. Dies lässt sich aus der Definition dieser Spalten ableiten, und es ist unpraktisch, dass ein Nullwert für diese Messgrößen ungültig ist, z. B, Null für den Body-Mass-Index oder den Blutdruck ist ungültig.

Aber für dieses Tutorial werden Sie direkt die vorverarbeitete Version des Datensatzes verwenden.

# load dataurl = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"names = dataframe = pd.read_csv(url, names=names)

Sie haben die Daten jetzt in ein DataFrame-Objekt namens dataframe geladen.

Lassen Sie uns das DataFrame-Objekt in ein NumPy-Array umwandeln, um eine schnellere Berechnung zu erreichen. Außerdem sollten wir die Daten in separate Variablen aufteilen, damit die Merkmale und die Beschriftungen getrennt sind.

array = dataframe.valuesX = arrayY = array

Wunderbar! Sie haben Ihre Daten vorbereitet.

Zunächst werden Sie einen statistischen Chi-Quadrat-Test für nicht-negative Merkmale implementieren, um 4 der besten Merkmale aus dem Datensatz auszuwählen. Sie haben bereits gesehen, dass der Chi-Quadrat-Test zur Klasse der Filtermethoden gehört. Wenn jemand neugierig auf die Interna von Chi-Squared ist, leistet dieses Video hervorragende Arbeit.

Die scikit-learn-Bibliothek bietet die Klasse SelectKBest, die mit einer Reihe verschiedener statistischer Tests verwendet werden kann, um eine bestimmte Anzahl von Merkmalen auszuwählen, in diesem Fall ist es Chi-Squared.

# Import the necessary libraries firstfrom sklearn.feature_selection import SelectKBestfrom sklearn.feature_selection import chi2

Sie haben die Bibliotheken importiert, um die Experimente durchzuführen. Jetzt wollen wir sie in Aktion sehen.

# Feature extractiontest = SelectKBest(score_func=chi2, k=4)fit = test.fit(X, Y)# Summarize scoresnp.set_printoptions(precision=3)print(fit.scores_)features = fit.transform(X)# Summarize selected featuresprint(features)

 ]

Interpretation:

Sie können die Punktzahlen für jedes Attribut und die 4 ausgewählten Attribute (die mit den höchsten Punktzahlen) sehen: plas, test, mass und age. Diese Punktzahlen werden Ihnen helfen, die besten Merkmale für das Training Ihres Modells zu bestimmen.

P.S.: Die erste Zeile gibt die Namen der Merkmale an. Für die Vorverarbeitung des Datensatzes wurden die Namen numerisch kodiert.

Als Nächstes werden Sie die rekursive Feature-Elimination implementieren, die eine Art von Wrapper-Feature-Auswahlmethode ist.

Die rekursive Feature-Elimination (oder RFE) funktioniert durch rekursives Entfernen von Attributen und Erstellen eines Modells auf den verbleibenden Attributen.

Sie verwendet die Modellgenauigkeit, um festzustellen, welche Attribute (und Kombinationen von Attributen) am meisten zur Vorhersage des Zielattributs beitragen.

Sie können mehr über die Klasse RFE in der scikit-learn-Dokumentation erfahren.

# Import your necessary dependenciesfrom sklearn.feature_selection import RFEfrom sklearn.linear_model import LogisticRegression

Sie werden RFE mit dem Logistic Regression-Klassifikator verwenden, um die drei besten Merkmale auszuwählen. Die Wahl des Algorithmus spielt keine große Rolle, solange er geschickt und konsistent ist.

# Feature extractionmodel = LogisticRegression()rfe = RFE(model, 3)fit = rfe.fit(X, Y)print("Num Features: %s" % (fit.n_features_))print("Selected Features: %s" % (fit.support_))print("Feature Ranking: %s" % (fit.ranking_))

Num Features: 3Selected Features: Feature Ranking: 

Sie können sehen, dass RFE die Top 3 Features als preg, mass und pedi ausgewählt hat.

Diese sind im Support-Array mit „True“ und im Ranking-Array mit einer „1“ markiert. Dies wiederum zeigt die Stärke dieser Merkmale an.

Als Nächstes werden Sie die Ridge-Regression verwenden, die im Grunde eine Regularisierungstechnik und eine eingebettete Merkmalsauswahltechnik ist.

Dieser Artikel gibt Ihnen eine ausgezeichnete Erklärung zur Ridge-Regression. Sieh ihn dir auf jeden Fall an.

# First things firstfrom sklearn.linear_model import Ridge

Als Nächstes wirst du die Ridge-Regression verwenden, um den Koeffizienten R2 zu bestimmen.

Sieh dir auch die offizielle Dokumentation von scikit-learn zur Ridge-Regression an.

ridge = Ridge(alpha=1.0)ridge.fit(X,Y)

Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None, normalize=False, random_state=None, solver='auto', tol=0.001)

Um die Ergebnisse der Ridge-Regression besser verstehen zu können, wirst du eine kleine Hilfsfunktion implementieren, die dir helfen wird, die Ergebnisse in einer besseren Form zu drucken, damit du sie leicht interpretieren kannst.

# A helper method for pretty-printing the coefficientsdef pretty_print_coefs(coefs, names = None, sort = False): if names == None: names = lst = zip(coefs, names) if sort: lst = sorted(lst, key = lambda x:-np.abs(x)) return " + ".join("%s * %s" % (round(coef, 3), name) for coef, name in lst)

Als Nächstes werden Sie die Koeffiziententerme des Ridge-Modells an diese kleine Funktion übergeben und sehen, was passiert.

print ("Ridge model:", pretty_print_coefs(ridge.coef_))

Ridge model: 0.021 * X0 + 0.006 * X1 + -0.002 * X2 + 0.0 * X3 + -0.0 * X4 + 0.013 * X5 + 0.145 * X6 + 0.003 * X7

Sie können alle Koeffiziententerme erkennen, die mit den Merkmalsvariablen verbunden sind. Dies wird Ihnen wiederum helfen, die wichtigsten Merkmale auszuwählen. Im Folgenden finden Sie einige Punkte, die Sie bei der Anwendung der Ridge-Regression beachten sollten:

• Sie wird auch als L2-Regularisierung bezeichnet.
• Für korrelierte Merkmale bedeutet dies, dass sie dazu neigen, ähnliche Koeffizienten zu erhalten.
• Merkmale mit negativen Koeffizienten tragen nicht so viel bei. Aber in einem komplexeren Szenario, in dem Sie mit vielen Merkmalen zu tun haben, wird Ihnen dieser Wert bei der endgültigen Entscheidungsfindung für die Auswahl der Merkmale auf jeden Fall helfen.

So, damit ist der Abschnitt über die Fallstudie abgeschlossen. Die Methoden, die Sie im obigen Abschnitt eingeführt haben, werden Ihnen helfen, die Merkmale eines bestimmten Datensatzes umfassend zu verstehen. Ich möchte Ihnen einige kritische Punkte zu diesen Techniken nennen:

• Die Auswahl der Merkmale ist im Wesentlichen ein Teil der Datenvorverarbeitung, die als der zeitaufwändigste Teil jeder Pipeline für maschinelles Lernen gilt.
• Diese Techniken werden Ihnen helfen, systematischer und maschinenlernfreundlicher vorzugehen. Sie werden in der Lage sein, die Merkmale genauer zu interpretieren.

Fassen Sie zusammen!

In diesem Beitrag haben Sie eines der am besten untersuchten und erforschten statistischen Themen behandelt, nämlich die Merkmalsauswahl. Sie haben sich auch mit den verschiedenen Varianten vertraut gemacht und sie verwendet, um zu sehen, welche Merkmale in einem Datensatz wichtig sind.

Sie können dieses Tutorial weiterführen, indem Sie ein Korrelationsmaß in die Wrapper-Methode einbinden und sehen, wie es funktioniert. Im Laufe der Handlung werden Sie vielleicht Ihren eigenen Mechanismus zur Auswahl von Merkmalen entwickeln. Auf diese Weise schaffen Sie die Grundlage für Ihre kleine Forschung. Die Forscher verwenden auch verschiedene Soft-Computing-Prinzipien, um die Auswahl durchzuführen. Dies ist ein ganzes Studien- und Forschungsgebiet für sich. Außerdem sollten Sie die vorhandenen Algorithmen zur Merkmalsauswahl an verschiedenen Datensätzen ausprobieren und Ihre eigenen Schlüsse ziehen.

Warum haben diese traditionellen Methoden zur Merkmalsauswahl immer noch Bestand?

Ja, diese Frage ist offensichtlich. Denn es gibt neuronale Netzarchitekturen (z.B. CNNs), die durchaus in der Lage sind, die wichtigsten Merkmale aus den Daten zu extrahieren, aber auch das hat eine Einschränkung. Die Verwendung eines CNN für einen regulären Tabellendatensatz, der keine spezifischen Eigenschaften aufweist (die Eigenschaften, die ein typisches Bild hat, wie Übergangseigenschaften, Kanten, Positionseigenschaften, Konturen usw.), ist nicht die klügste Entscheidung. Wenn Sie nur über begrenzte Daten und Ressourcen verfügen, kann das Training eines CNN auf regulären Tabellendatensätzen zu einer völligen Verschwendung werden. In solchen Situationen sind die von Ihnen untersuchten Methoden auf jeden Fall nützlich.

Wenn Sie sich näher mit diesem Thema befassen möchten, finden Sie hier einige Ressourcen:

• Feature Selection for Knowledge Discovery and Data Mining
• Subspace, Latent Structure, and Feature Selection: Statistical and Optimization Perspectives Workshop
• Feature Selection: Problem statement and Uses
• Using genetic algorithms for feature selection in Data Analytics

Nachfolgend sind die Referenzen aufgeführt, die für die Erstellung dieses Tutorials verwendet wurden.

• Data Mining: Concepts and Techniques; Jiawei Han Micheline Kamber Jian Pei.
• Eine Einführung in die Feature-Auswahl
• Analytics Vidhya Artikel über Feature-Auswahl
• Hierarchische und gemischte Modelle – DataCamp Kurs
• Feature-Auswahl für maschinelles Lernen in Python
• Ausreißer-Erkennung in Stream-Daten durch MachineLearning und Feature-Auswahl Methoden
• S. Visalakshi und V. Radha, „A literature review of feature selection techniques and applications: Review of feature selection in data mining,“ 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, 2014, pp. 1-6.