Wir können Gibbs-Helmholtz verwenden, um die Temperaturabhängigkeit von \(K\)
\}{∂T} \right)_P = \dfrac{-Δ_rH^o}{T^2}\]
Im Gleichgewicht können wir \(Δ_rG^o\) mit \(-RT\ln K\) gleichsetzen, sodass wir erhalten:
\}{∂T} \right)_P = \dfrac{Δ_rH^o}{RT^2}
Wir sehen, dass es davon abhängt, ob \(K\) mit der Temperatur zunimmt oder abnimmt, ob die Reaktionsenthalpie positiv oder negativ ist. Wenn sich die Temperatur so wenig ändert, dass \(Δ_rH^o\) als konstant angesehen werden kann, können wir einen \(K\)-Wert bei einer Temperatur durch Integration des obigen Ausdrucks in eine andere übersetzen und erhalten eine ähnliche Ableitung wie bei der Schmelzpunktsenkung:
\
Wenn mehr Präzision erforderlich ist, können wir die Temperaturänderungen von ΔrHo durch Verwendung von Wärmekapazitätsdaten korrigieren.
Wie \(K\) mit der Temperatur zu- oder abnimmt, hängt damit zusammen, ob die Reaktionsenthalpie positiv oder negativ ist.
Der Ausdruck für \(K\) ist eine ziemlich empfindliche Funktion der Temperatur, da er exponentiell von der Differenz der stöchiometrischen Koeffizienten abhängt Eine Möglichkeit, die empfindliche Temperaturabhängigkeit der Gleichgewichtskonstanten zu erkennen, ist, sich daran zu erinnern, dass
\
jedoch, da unter konstantem Druck und konstanter Temperatur
\
Die Gleichung \(\ref{18}\) wird
\
Nimmt man den natürlichen Logarithmus beider Seiten, so erhält man eine lineare Beziehung zwischen \(\ln K \) und den Standardenthalpien und -entropien:
\
, die als van’t-Hoff-Gleichung bekannt ist. Sie zeigt, dass eine Darstellung von \(\ln K\) gegen \(1/T\) eine Linie mit der Steigung \(-\Delta_r{H^o}/R\) und dem Schnittpunkt \(\Delta_r{S^o}/R\) sein sollte.
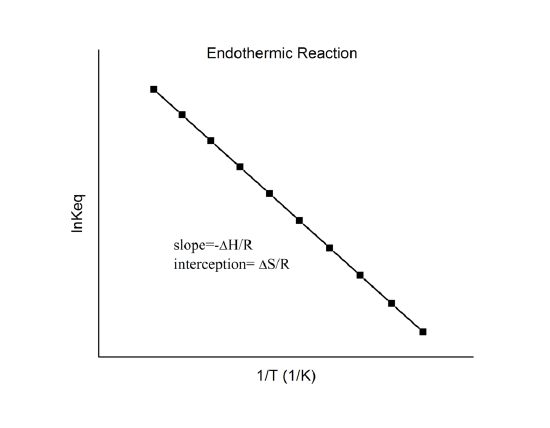
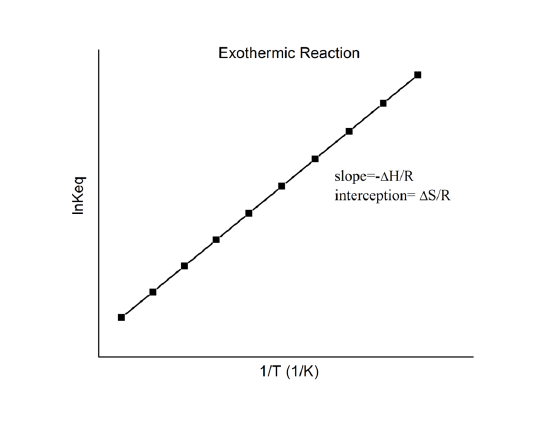
Diese Größen können also aus den Daten \(\ln K\) vs. \(1/T\) ohne Kalorimetrie bestimmt werden. Natürlich ist die Hauptannahme hier, dass \(\Delta_r{H^o}\) und \(\Delta_r{S^o}\) nur sehr schwach von \(T\) abhängen, was in der Regel zutrifft.